不含时薛定谔方程和能量分立的原因

首先需要理解什么是 "不含时"
在量子力学里, 对于单个粒子, 我们只关心它在哪个位置出现的几率有多大, 而波函数在现实里是不存在的, 波函数只是恰好用来描述粒子非常好而使用而已
那么实际上我们关心的只是一个概率函数, 用来描述粒子在某处出现的概率有多大, 并且这个函数也必定是实函数, 而假设 ψ(x,t) 是一个波函数, 那么 |ψ(x,t)|^2 就恰好是我们关心的概率函数
"不含时" 的意思是说概率函数不随时间变化而变化, 这就表明这个粒子找到了一个比较稳定的状态. 而概率函数不随时间变化而变化的话, 这时候我们也就可以假设对应的波函数也不会随时间变化而变化, 而且因为概率是实值, 所以我们也可以设波函数是实值的, 但是看到原来的薛定谔方程, 里面有时间又有复数, 很难想象怎么找到一个不含时的实值解, 所以为了描述 "不含时波函数" 我们需要不含时薛定谔方程

从含时变为不含时
看到含时薛定谔方程:

我们的目标就是根据一定条件求解里面的ψ(x,t)
而我们是假设 ψ 与时间无关(不随时间变化而变化), 所以我们可以把ψ分成两部分 ψ(x,t) = φ(t)*Φ(x) (分离变量法), 这时Φ就是我们需要的不含时波函数了, 但是, 单独一个Φ是不符合薛定谔方程的, 所以这时候需要合适的变换:
把ψ= φ*Φ代入薛定谔方程中, 并且把微分无关的全部扔到微分外

然后两边同时除以ψ

可以看到方程的左边只与位置x有关, 方程右边只与时间有关, 这两部分相等就证明左右两边应该等于一个不与变量有关的常数
而推导含时薛定谔方程时就已经知道: ih*∂Ψ/∂t = EΨ, 而现在等式的右边就等于 E , 而E就是能量, 于是就有:

两边同乘Φ后:
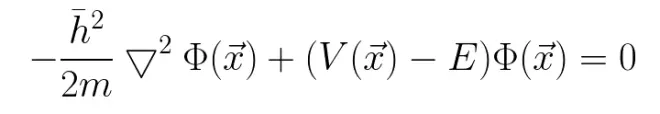
这个就是不含时薛定谔方程了

能量分立的原因
学过数理方程的人应该可以一眼看出: 不含时薛定谔方程是S-L方程, 一定条件下必定存在分立解
但是为了照顾未学过数理方程的读者, 这里举一个例子:

在一维中, 势V在0<=x<=1等于0, 其他地方等于正无穷 (一个非常简单的无限深井势)

然后我们来根据不含时薛定谔方程求解在这个势中的波函数Φ
假设我们一开始就知道 "粒子总会趋向势低的地方移动", 所以在[0,1]外的波函数必定为0, 就算我们一开始不知道这个事实, 数学也不会允许在[0,1]外的值不等于0的
而在[0,1]内势为0, 我们可以把势V和不含时薛定谔方程一起写成比较简便的形式:

下面来求解 上面的式子: 稍微调整一下系数得

求解等式在高数里应该也有给出的, 但是被指数函数洗脑的我有不同的见解(这个弯路绕得非常远, 推荐忽略不看)


并且波函数必定是连续函数 (只要粒子被观察的一瞬间, 因为波函数坍塌才会形成不连续波函数, 而观察后也会马上恢复连续), 在[0,1]外波函数值为0, 那么为了确保波函数的连续性, 有: ψ(0) = ψ(1) = 0
由ψ(0)=0 知道, A必须为0, 那么波函数变为:

已知B不为0 (B为0的话还玩什么啊), 那么有把ψ(1)=0代入:

解得:

归一化: 概率函数的积分必须为1 (总概率为嘛....):

解得: B=√2, 于是波函数为:

其中, 对应的能量为:


从上述过程可以看出, 能量分立的原因是在解S-L方程中产生的, 而正是因为数学是表达现实的方式之一, 所以事实上能量也确实是分立的
简单来说, 薛定谔方程表达了某种现实规律, 而求解薛定谔方程其实就算寻找符合规律的东西, 而在这里求解的结果就是: 只有能量取某些分立的值才能符合这个规律, 而不符合规律的能量也是不存在的

