高数-极限三大核心应用,一个视频搞定!

大饼老师 | 1-4 极限的应用


无穷小的比较
极限的四则运算法则
若lim f (x)= A, lim g (x)= B,则有
(1)lim[f(x)±g(x)] = lim f(x)± lim g(x)=A±B
(2)lim[f(x)g(x)]= lim f(x)·lim g(x)=AB

应用1:无穷小的比较

注:■指的是有限值x₀或无穷大∞
例如:limx→0 x²=0 limx→1/x =0
正确认知:无穷小不是一个数,它是一个变量
零也是一个无穷小

1.2无穷小比较:无穷小趋向于0的速度快慢的比较
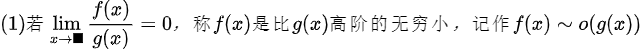
limx→0 x³/x²=limx→0 x=0

limx→0 x²/x³=limx→0 1/x =∞

limx→3 x²-9/x-3 =limx→0 (x+3)=6

limx→0 1-cosx/x² =1/2

。limx→0 sinx/x =1
注:f(x)和g(x)是同一个自变量x的变化过程中的无穷小,且g(x)≠0.
常见等价无穷小(必背)
x→0
sinx ~ x
tanx~x
arcsinx ~ x
arctanx ~ x
ln(1+x) ~ x
eˣ-1 ~ x
1-cosx ~ 1/2x²
aˣ-1 ~ xlna
(1+x)ᵃ-1 ~ ax

题型1:求极限
(1)确定型:代入法
(2)分式型未定型:找等价无穷小
(3)分式型未定型:提tanx
注意:当无穷小加减无穷小,不能用等价无穷小。只有乘法或除法可以替换。

使用等价无穷小替换的注意事项:
(1)无穷小才能替换,即x→0,如习题(1) limx→1 tanx/x
(2)方块思维(整体观),如习题(2)limx→3
(3)当无穷小量相加减时,不可将其中任意一个进行替换,如习题(3)limx→0 tanx-sinx /x³
乘除用等价无穷小替换,加减用麦克劳林替换
题型2:无穷小比较
设f(x)= 2ˣ+3ˣ-2,则当x→0时
A. f(x)是x的等价无穷小量
B. f(x)与x同阶但非等价无穷小量✓
C. f(x)是比x较高阶无穷小量
D. f(x)是比x较低阶无穷小量
- 第一步:判断出是未定型
- 第二步:判断出是分式型
- 第三步:用极限的加法运算,拆成两个极限,再找等价无穷小


注:■指的是有限值x₀或无穷大∞.
lnx < xᵃ <xᵇ < cˣ <<dˣ <<x! << xˣ(x→+∞,0<a<b,1<c<d)
2️⃣函数连续与间断


(1)有定义
(2)有极限
(3)极限值等于函数值
连续特点:—笔画
2. 间断点定义:
设函数f(x)在点x₀某去心领域内有定义,如果函数f(x)有下列三种情况之一,
(1)在x = x₀没有定义;


就称f(x)在x₀处不连续,或点x称为函数f(x)的不连续点或间断点

间断特点:不是一笔画
第一类间断点(左、右极限都存在)
(1)可去间断点


(2)跳跃间断点


第二类间断点(左、右极限至少一个不存在)
(1)无穷间断点


(2)振荡间断点



间断点判断的两步法:
(1)寻找间断点
- 函数定义域边界
- 分段函数分界点
(2)算左右极限


- 第一步:找间断点:定义域
- 第二步:算左右极限
3️⃣函数的渐近线
渐近线:曲线上一点M沿曲线无限远离原点或无限接近间断点时,如果M到一条直线的距离无限趋近于零,那么这条直线称为这条曲线的渐近线。
- 水平渐近线
- 斜渐近线
- 铅直渐近线
(1)水平渐近线:


(2)斜渐近线:


(3)铅直渐近线:



- 水平渐近线:y=c,c = lim x→∞ f(x)
- 分母→∞,f(x)→0
- 铅直渐近线:x=a,lim x→a f(x)=∞
- f(x)是分式,让分母=0
总结

家庭作业





