（合计431字，用时40min——）

第三章 多维随机变量及其分布

& 2 边缘分布

概念：

• 边缘分布函数：二维随机变量(X,Y)作为一个整体，具有分布函数F(X,Y)。而X和Y都是随机变量，各自也有分布函数，将它们分别即为FX(x)，FY(y)，依次称为二维随机变量(X,Y)关于X和关于Y的边缘分布函数。

• 离散型随机变量的边缘分布函数：
  

• (X,Y)关于X和关于Y的边缘分布律：
  

    ——分别称pi.(i=1,2,...)和p.j(j=1,2,...)为(X,Y)关于X和关于Y的边缘分布律

    （注意，记号中的“.”表示pi.是由pij关于j求和后得到的；同样，p.j是由pij关于i求和后得到的）。

• 连续型随机变量的边缘分布函数：
  

• (X,Y)关于X和关于Y的边缘概率密度：

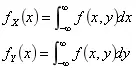
    ——分别称fX(x)，fY(y)为(X,Y)关于X和关于Y的边缘概率密度。

• 服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布：
  

    ——其中μ1,μ2,σ1,σ2,ρ都是常数，且σ1>0,σ2>0,-1<ρ<1，

    ——称(X,Y)为服从参数为μ1,μ2,σ1,σ2,ρ的二维正态分布，记为