切线指一条刚好触碰到曲线上某一点的直线

牛顿288、切线指一条刚好触碰到曲线上某一点的直线

 

导数（百度百科）：

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。

…导：见《欧几里得7》…

（…《欧几里得》：小说名…）
…数：见《欧几里得15》…

…derivative（英语）：n.（名词）派生词；衍（yǎn）生物；衍生字；派生物。

adj.（形容词）模仿他人的；缺乏独创性的…

[…生：见《伽利略28》…

（…《伽利略》：小说名…）

…衍、衍生：见《富田兴合苑业主的大事小事7》…

（…《富田兴合苑业主的大事小事》：小说名…）

 

dx什么意思？？——网友提问

2019-09-07，想玩游戏的猫：d（x）代表对x求微分。

dy/dx 中的d是“微小的增量”的意思，也就是指微小的增量y除以微小的增量x。在函数中是，微分的意思。

dx就是对x的微分，是把增量细微化，dx就是很小很小的一个x。

——《牛顿3》]

 

…微、商、微商：见《牛顿284》…

 

当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f'（x0）或df（x0）/dx。

…函、数、函数：见《欧几里得52》…

…极、限、极限：见《欧几里得218~280》…

导数是函数的局部性质。

…性、质、性质：见《欧几里得37》…

 

一个函数在某一点的导数描述了这个函数在这一点附近的变化率。

…描、述、描述：见《伽利略34》…

…变、化、变化：见《伽利略10》…

…率：见《欧几里得58》…

如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

…实、数、实数：见《欧几里得37》…

…切：见《牛顿44》…

…线：见《欧几里得175》…

 

切线（百度百科）：几何上，切线指的是一条刚好触碰到曲线上某一点的直线。

更准确地说，当切线经过曲线上的某点（即切点）时，切线的方向与曲线上该点的方向是相同的。

平面几何中，将和圆只有一个公共交点的直线叫做圆的切线。

 

几何定义

…几、何、几何：见《欧几里得28》…

…定、义、定义：见《欧几里得28》…

 

P和Q是曲线C上邻近的两点，P是定点，当Q点沿着曲线C无限地接近P点时，割线PQ的极限位置PT叫做曲线C在点P的切线，P点叫做切点；经过切点P并且垂直于切线PT的直线PN叫做曲线C在点P的法线（无限逼近的思想）。

…思、想、思想：见《欧几里得154》…

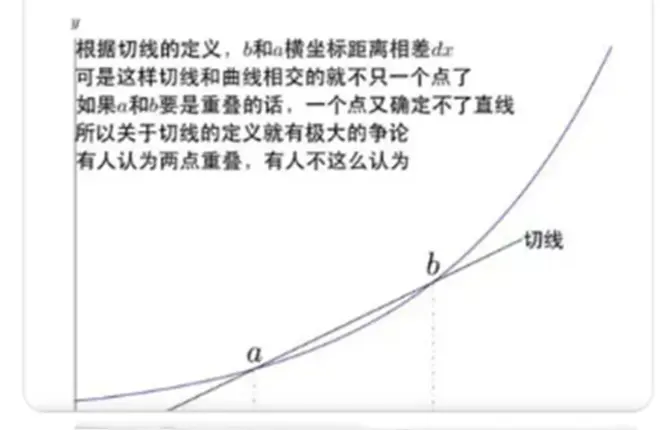
说明：平面几何中，将和圆只有一个公共交点的直线叫做圆的切线。这种定义不适用于一般的曲线；PT是曲线C在点P的切线，但它和曲线C还有另外一个交点；相反，直线l尽管和曲线C只有一个交点，但它却不是曲线C的切线。

 

代数定义

…代、数、代数：见《欧几里得36》…

 

在高等数学中，对于一个函数，如果函数某处有导数，那么此处的导数就是过此处切线的斜率。

该点和斜率所构成的直线，就为该函数的一个切线。

 

“斜（百度百科）：形声。从斗，从余，余亦声。

“斗”指家用舀水器具，“余”意为“剩下”。

“余”和“斗”联合起来表示“用斗倒水时剩余一部分”。

请看下集《牛顿289、斜、率、斜率，正、切、正切》”

若不知晓历史，便看不清未来

欢迎关注哔哩号“中国崛起呀”