试译 | “菱形系列”导论——海杜克《美杜莎的面具》

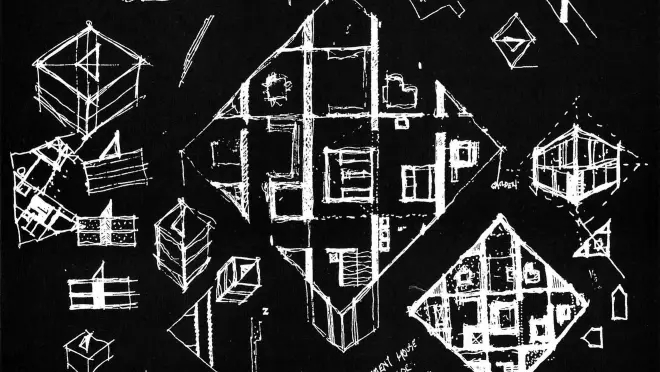
以下为尝试翻译稿，请谨慎阅读。如有误导，概不负责。

十九世纪二十年代，最终导致风格派特奥·凡·杜斯堡与彼埃·蒙德里安决裂的主要争论在于，凡·杜斯堡在画布上将内在直角关系倾斜45度，从而打破了最初与画布边界平行的90度关系。

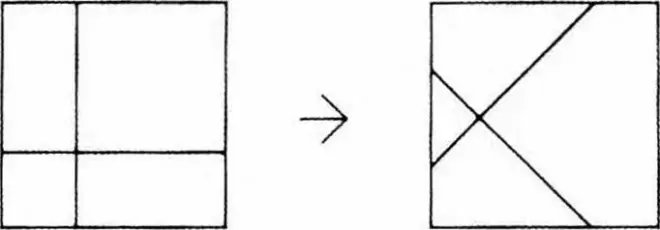
菱形项目是在建筑中探索上述形式可能性的首次尝试。一系列的问题浮现出来。不过，在进入这些讨论之前，关于立体主义空间转译到建筑，有几点需要说明。其中包括，立体派画家们对画布上图形的强烈集中，而随着图面的深浅画布边缘的活动逐渐减少感兴趣；对正90度、60度、30度、45度轴网以及平面图形的联结关系感兴趣。建筑师勒·柯布西耶在空间问题上认识到立体主义的理念。哈佛大学的卡朋特中心是将立体主义空间问题转译到建筑的最佳诠释。在19世纪早期的哈贝住宅和兰格住宅中，密斯·凡·德·罗对抽象的平面概念和将平面作为二维（图形）问题处理所涉及的空间矩阵的概念表现出了同等的兴趣。

对于蒙德里安极力主张的直角关系的重要性，这一动作引发了一系列形式争论。蒙德里安对凡·德斯堡45度内部关系的回答是倾斜画布，但对观察者而言仍旧保持90度内部直角关系。这一动作的形式结果是令人震惊的：边缘和轮廓的外围张力被加强，领域的延伸被暗示超出画布之外。就建筑的空间意义而言，这一观点的理念还还没有得到试验。

蒙德里安一开始是一位立体主义者，后来又从立体主义转向了新造型主义。他不断地敦促建筑师们研究他绘画中的空间概念；然而，他那个时代的建筑师显然对采用菱形“构型”并不感兴趣。当今建筑学的主要争论之一仍然是关于二维空间和三维空间概念之间的辩证关系。

勒·柯布西耶早期的建筑，如加歇别墅，是建筑形式二维平面化的宏伟构想，但由于坚持单一的优先视角而显得有些奇怪；立面以平面构图的形式呈现在观察者的眼前，与平面图非常相似。其立面，有对文艺复兴式外部形式视图的回溯，即在二维表皮上构图的问题。

建筑的独特之处不仅仅在于呈现完美的平面式立面，或创造在倾斜、夸张的深透视中盘旋的精致建筑体量。

如果说立体主义绘画为（20世纪）20年代的建筑师提供了思想，那么蒙德里安的菱形绘画对今天的建筑师来说可能会有一些意义。在菱形项目中，探求以一种新的投影和分解空间形式的初始空间演化。另一种空间和形式的观察方式可以被采用。文艺复兴式的透视空间是一种事实；蕴含流动空间的后立体主义浅-平空间也是一种事实。

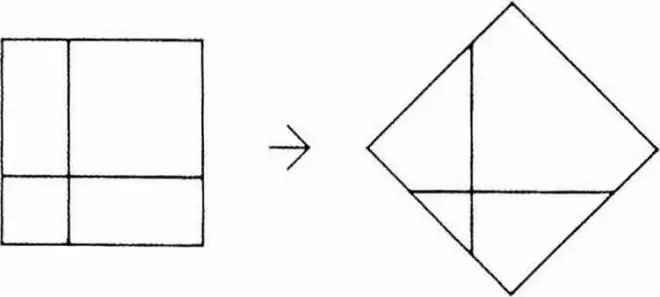
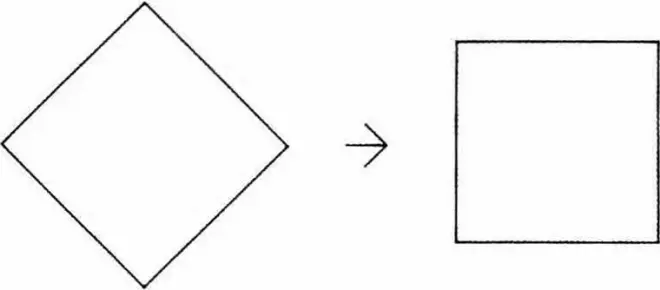
当平面图中的菱形被等轴测投影时，它就变成了正方形。这似乎是一个不言自明的事实。但在这些探索之前，这种投影，即把菱形投影到正轴测，从未出现在建筑图纸中。而反向的操作却已经存在和使用了，也就是，正方形在等轴测中绘制成菱形。

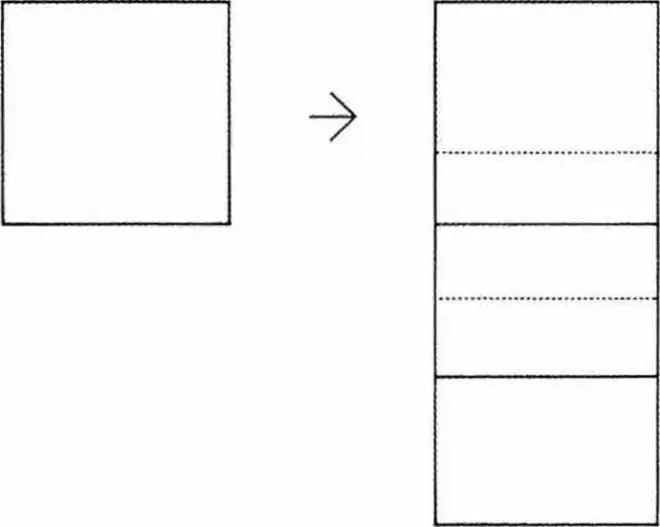
当平面上的一个正方形用轴测画出来时，在眼睛看来它就像是一个三维投影。当一层以上的平面以等轴测投影时，它会非常自然地建造起来，并且仍然呈现为三维表现。当菱形以等轴测绘制且平面不止一层时，就会出现一种非常特殊的现象。这些形式看起来像是二维的；这些楼层在先在的二维视图中相互重叠。在等轴测中，形式向画布平面倾斜；它们是三维的，但更强的二维读解却占据主导地位。（这里不理解的可以去看特奥·凡·杜斯堡《不和谐音对位构图》）二维图形相互咬合堆叠是我们最熟悉不过的现象了。

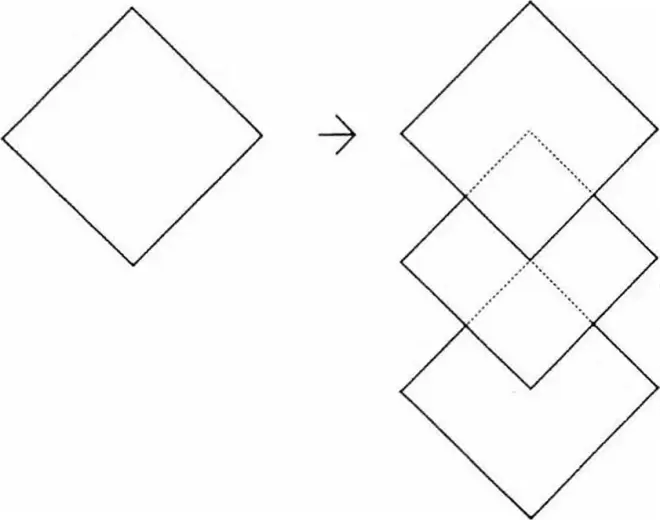
正如立体派画家在他们的绘画中将物体向绘画平面（画面）倾斜一样，菱形的等轴侧投影也为建筑图纸提供了类似的视角。菱形的等轴侧投影正是建筑中的立体投影，从而完善了绘画中的立体投影与建筑中的立体投影的形式关系。

使用菱形等距轴测，摒弃古老过时的透视投影形式，将把空间的质量传递给观察者。平面图的二维性投射到三维等轴测后，仍然保持二维，但更接近平面图的二维抽象，或许也更接近建筑空间的实际的二维性。

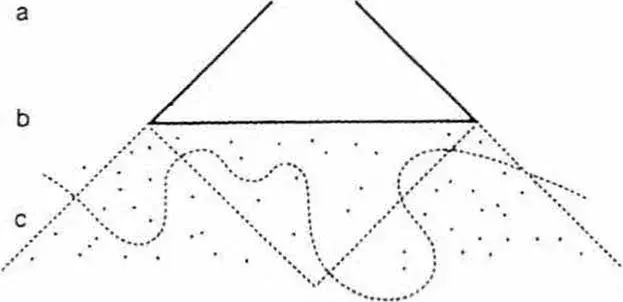
关于菱形构型的实际三维空间，引发了一些的问题，并带来了侧向边界的延伸和视角。二维表皮和立面的呈现并不是唯一的，它意味着正面和单一的视角。也许，建筑空间的历史可以用图7来表示，其中a表示过去，b表示现在，c表示未来。

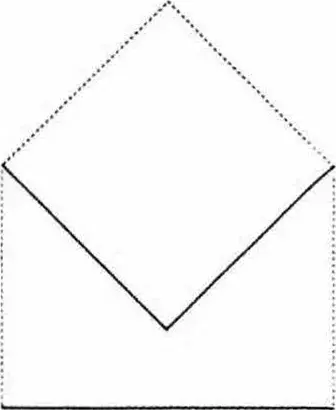
未来只能靠推测。当观察者站在菱形外部，从顶点的外侧观察(图8)，则其两条边（面）会有向前展平的趋势，从而产生了一个侧边延展的扩展透视视图。在内部(图9)，观察者也面临非常相似的现象，尽管它是情境的内化；他再次被展平的两个面所环绕。这里体现出内部与外部体验的一种协调。其中最重要的点在于相交的直角关系；曲面会弱化这一体验和效果。张力来自垂直和水平直线的对立，蒙德里安在关于绘画的讨论中小心翼翼地指出了这一点；圆显得有点可疑，但也不完全是；对立有时是必要的。

在菱形领域中引入直角，带来了观察者面对不断延伸的边界开始菱形“探索”的可能性。这一结论支持最大程度的“放松”源自最大程度的“收紧”的观点；以及垂直于观察者的视角观看空间，而成角度地观看侧立面。以上是关于将菱形架构引入建筑空间生成“家族”的有些简短的讨论。

以下：英文原文

One of the major arguments which eventually caused the disengagement of the De Stijlists, Theo Van Doesburg and Piet Mondrian, during the nineteen twenties was when Van Doesburg tipped by 45 degrees the internal right angle relationships within the canvas, thereby destroying the original internal 90 degrees which ran parallel with the edge of the canvas.

The Diamond Projects are a first attempt to investigate the above formal possibilities in architecture. A number of problems emerge; however, before going into these, a few points as the Cubist space translated into architecture should be made. Among other things the Cubist painters were interested in the strong centralization of figures upon the canvas, with a decrease of activity towards the periphery of the field along with the problems of shallow depth; and the strong 90, 60, 30, 45 degree gridings and the interlocking of planar figures. The architect, Le Corbusier, was cognizant of the Cubist ideas as far as spatial problems. The Carpenter Center at Harvard is a prime rendition of the problems of Cubist space translated into architecture. Mies van der Rohe in the Hubbe and Lange houses of the eatrly part of the century shows equal interest in the idea of an abstract plan and the spatial matrix involved in the treatment of plan as a two-dimensional problem.

This act caused a serious formal disagreement with regard to the significance of right angle relationships in which Mondrian was actively and spiritually involved. Mondrian's answer to Van Doesburg’s 45 degree internal relationship was to tip the canvas, but still maintain the internal right angle 90 degree relationships as far as the observer was concerned. The formal ramifications of this action were shattering: the peripheric tension of the edge and contours were heightened and the extension of field was implied beyond the canvas. The ideas in this point of view were not experimented with as far as the spatial implications in architecture were concerned.

Yet Mondrian worked first as a Cubist, and then moved from Cubism into Neo-Plasticism. He continually urged architects to delve into the spatial ideas of his paintings; however, the architects of his time apparently were not interested in adopting the diamond configuration. One of the major architectural arguments of today still concerns the dialectic between the concepts of two-dimensional and three-dimensional space.

Le Corbusier's earlier buildings such as Villa Garches were magnificent conceptions of the flat two-dimensional aspect of architectural form, yet are curious because of the insistence of a single preferred point of view; the facade is presented as flat composition to the eye of the observer, very much like the plans. There is in the elevation a recall of the Renaissance vision of external form, the problem of composing upon a two-dimensional surface.

The uniqueness of architecture does not lie only in the presenting of a perfectly flat facade or in the creation of an elaborate volumetric building spiralling in oblique exaggerated deep perspectives.

If the Cubist canvas provided thought to the architects of the twenties, there may be some significance in the diamond canvases of Mondrian for architects today. The initial spatial evolution in the form of a new projected and exploded space were sought after in the Diamond Projects. Another way of looking at space and form can be adapted. The Renaissance space of perspective is a fact; the flat-shallow contained flux space of the post-Cubist canvas is a fact.

When a diamond form in plan is projected by isometric it becomes a square. This may appear to be a self-evident truth, but such projections, that is, the projections of diamond forms into isometrics, had not appeared in architectural drawings prior to these explorations. The converse has been in existence and use, that is, the square drawn in isometric which becomes a diamond.

When a square form in plan is drawn in isometric it appears to the eye as a three-dimensional projection. When more than one floor plan is projected in isometric, it builds up quite naturally and still appears as a three-dimensional representation. When the diamond is drawn in isometric and has a plan of more than one floor, a very special phenomenon occurs. The forms appear two-dimensional; the stories overlap each other in a primary two-dimensional vision. The forms tip forward in isometric towards the picture plane ; they are three-dimensional, yet a stronger reading of two-dimensionality predominates. A meshing together of two-dimensions pushing forward is the phenomenon we are most aware of.

As the Cubists in their paintings tipped objects forward towards the picture plane, the isometric projections of the diamond accomplished a similar point of view for architectural drawings. The isometric projections of the diamond are Cubist projections in architecture, therefore completing the formal relationship between Cubist projection in painting and Cubist projection in architecture.

The quality of space is transferred to the observer in the diamond isometrics without using the antique and outmoded form of perspective projection. The two-dimensionality of a plan, projected into the three-dimensional isometric, still appears two-dimensional, closer to the two-dimensional abstraction of the plan and perhaps closer to the actual two-dimensionality of the architectural space.

With regard to the actual three-dimensional space of the diamond configuration, certain problems arise and bring forth an aspect of encompassing lateral extension and vision. The presentation of a flat two-dimensional surface and facade is not unique, it implies frontality and a single point of view. Perhaps, the history of space in architecture can be represented in Figure 7, in which a denotes the past, b, the present and c, the future.      

Futures can only be speculated upon. When the observer is external to the diamond, looking at the outside of the apex (Fig. 8), there is a tendency of the two sides to come forward and flatten out, an extended perspective of lateral extension and vision is produced. Internally (Fig. 9), the observer is confronted with a very similar phenomenon although it is the internalization of the situation; he is again encompassed by the flattening out of the two sides; we have here the appearance of a coordination of external and internal experience. Of prime importance are the right-angle relationships of the intersections; a curvilinear surface would have the effect of softening the experience and impact. Tensions come from the opposition of straight lines, verticals and horizontals which Mondrian carefully points out in his discussions upon painting; the circle becomes somewhat suspect, but not entirely ; contradictions sometimes are necessary.

The introduction of the right angle within the diamond field permits the possibility of the observer to begin the trek of the diamond confronted with continual expanding encompassment. The conclusion permits the thesis of maximum extension from the maximum compression; that of seeing space perpendicular to the observer's vision; that is of seeing laterally the hypotenuse. The above is a somewhat compressed discussion for the admission of the diamond configuration into the family of architectural space generators.

1. 本篇英文原稿及插图均来自Mask of Medusa，by John Hejduk；

2. 更多相关翻译欢迎关注专栏或搜索个人公众号IDsCeLeee；