Heise method是一种相对小众但效率很高的魔方解法，它能在不借助任何公式、不尝试多种可能的情况下，平均在40步内复原三阶魔方（语出Sebastiano Tronto，Fewest Moves Tutorial），其思路对于魔方最少步项目（Fewest Moves Challenge，FMC）特别有借鉴意义，同时也发展出了可应用于速拧的Speed-Heise公式集（作者Matt DiPalma，详见https://www.speedsolving.com/wiki/index.php/Speed-Heise）。

    Heise method作者Ryan Heise的网站（https://www.ryanheise.com/cube）有该法详细文字教程和一些魔方知识（包括转换机、筑块、降群原理等），以及诸多动图（是虚拟魔方播放器，不是gif动图，但本文只能用gif形式截取，因此墙裂建议访问原站，体验更佳）。目前Heise method中文资料较少，网页机翻又词不达意，于是我一面学习，一面便想斗胆做一些翻译和整理。

    本系列专栏中，我将意译Heise method（下称“Heise法”）教程全文，同时夹带私货（算是学习笔记，会用蓝字标注出来的XD）。水平有限，还望魔友们多多指教～

本节详解转换机和共轭原理，此二者广泛应用在盲拧与最少步解法中，不理解它们将无法完全掌握Heise法，反而跌入死记硬背的窠臼。可惜Ryan Heise的教程中关于转换机的内容还是有限的，只详细讲了Heise法相关的一种角块三循环。且原教程中超级精炼的插图和理论化的文风给理解增加了不少难度……

因此，我首推平台上各路高手关于转换机的视频教程（就拿我看过的视频来说，轻松聊天款可找「依旧是一九四」，系统教程款可找「Cuber-天下雨」，直观动画款可找「天方魔」……当然，主要是讨论正三阶魔方）。

转换机与共轭的结合较易理解。因此为压缩篇幅，我不按照原教程顺序翻译，而是先翻译转换机部分，中途再讲共轭。

    转换机（Commutators）可控制魔方上若干色块发生变化，并保持其他块均不受影响。所谓“转换机”其实是一串符合【X Y X’ Y’】格式的转动步骤序列（也可通俗地称之为“公式”，所以理解了转换机就能随时创造公式）。

X或Y代表一步或多步转动，加引号代表将对应转动逆序，例如X = R U L’，则X’ = L U’ R’，注意不是R’ U’ L；假如Y = B’，那么一条完整的转换机公式便是：(R U L’) B’ (L U’ R’) B。

PS：原文用上角标-1代表逆序，这里为方便显示改用引号。

    对于任意的X序列和Y序列，转换机只会影响这两个序列涉及的块的交集。如果X和Y完全不相交，分别影响魔方的不同位置，那么做完【X Y X’ Y’】后什么也不会发生。我们的思路是使X和Y的交集尽量小，但不为零（听懵了吗？先往下读再说/doge）。

    Heise法中可能用到转换机的地方有：

    1. 角块三循环（详解单空穴8步转换机，重中之重）

    2. 棱角对三循环

    3. 棱块三循环

    4. 角块原地翻转

1. 角块三循环

    角块三循环是指单独移动魔方上三个角块的位置（A到B，B到C，C到A），并保持其他块不动。

剧透一下，Heise法流程大致是筑伪块完成F2L-1——差一个空槽完成的前两层——再复原余下部分，但除了最后三个角块（Last Three Corners，L3C），所以最后一步往往需要使用一条转换机来复原整个魔方。

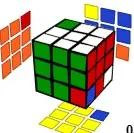
    以上图为例，魔方只有最后三个角块未复原（这就是Heise法最后一步会遇到的状态）。我们要做的第一步是：找出有两个角未复原的面，但这两个角中的一个必须色向正确。本例中黄色面是唯一的选择（黄橙绿角块位置错误但色向正确，黄色是朝下的；蓝白红角块位置和色向都错误）。

    接下来就要找出转换机的X和Y序列：

    ①X序列要做的是把黄橙绿角块搬到顶层，并同时把顶层错误的角块替换到它的位置上；因为这个块色向正确，所以后续可通过X’让它回到底层。

注意，X序列通常是R U* R’、F’ U* F之类的三步转动。

若着眼于底层，不难发现这三步转动只会影响底层的一个角块，这个角块可称为“空穴”，它就是XY两个序列的交集。

    ②Y序列要做的是进行一步底层调整，以在做X’之前，让蓝白红角块与周围色块拼好。做完这些步骤后三个角块就会同时复原。

如果以“空穴”为中心来理解，就是第①步使用3步转动让顶层角块来到“空穴”位置，第②步使用1步转动让底层角块来到“空穴”位置。于是3+1+3+1=8，形成了典型的8步转换机。

注意这条转换机的逆过程D F' U F D‘ F' U' F，同样是对这3个角块进行三循环，但循环的方向恰好相反。1+3+1+3也是理解8步转换机的一种方式。

    更多例子（建议自行思考后再下滑看解法）：

……

想出来了么？原理和上面的例子完全相同～

 ……

是时候引入共轭（Conjugate）的概念了。

    共轭是指形如【X Y X’】的转动步骤序列。这条ZBLL的U case公式就是一个典例：

R’ (F R U’ R’ U’ R U R’ F’ R U R’ U’ R’ F R F’) R

相当于在一条PLL的Y Perm公式前后各加上一步R’和R，就实现了与PLL不一样的效果。不过这么长的公式显然不是Heise法的风格，下面是原教程给出的例子。

    如果Y是下面这条公式，它可以改变三个角块的位置：

    同样是这条公式，还可以复原下面这个魔方，只要旋转一下蓝色面：

    以上全程便是【X Y X’】（这就一个共轭结构，注意X不一定只有一步；开头的X常被称为Setup，结尾的X’常被称为Reverse，特别是在盲拧领域）。

很多时候，角块三循环需要转换机和共轭相结合才能完成。

◆例1

    可选白红绿角块作为突破口，它的色向正确但位置错误。但用于替换它的角块必须在魔方的另一侧（而不能像本例都同一层内）。所以只需一步R2，就可以使用转换机了。

    注意第一步R2和第二步R可消为一步R’，所以这个例子实际上是使用9步复原。

◆例2

    本例中蓝色面所有色向都是正确的，但三个角块不是哪个都可选为“空穴”（被转换机X序列搬到顶层的那个块），因为X序列并不都能用3步完成。这种情况下考虑黄色或橙色面的色向或许是更好的选择。

2. 棱角对三循环

    理解了角块三循环后，只需把一组棱角对视为整体，便可将转换机的思路拓展到棱角对三循环（作者举出了12个例子，最边左一列是角块三循环；为方便对比，只写出[X,Y]格式的公式，就不截动图了）。

    v2v3的本质与v1相同，故一种情形可能有多种转换机可以解决，有时换一条转换机甚至可以减省共轭步骤（v1类型的转换机和左边的角块转换机是比较类似的，都影响了相同的3个角块）。

3. 棱块三循环

◆类型一（双空穴4步转换机）

    最短的转换机（桥式玩家的老熟人了），但实战中应用时可能会花费更多步骤做共轭。

◆类型二（单空穴8步转换机）

    与上述角块转换机类似（都是3+1+3+1=8步）。

4. 角块原地翻转（这里只讲了两角翻）

    一条转换机，可以使任意两个角块朝相反方向原地翻转（一个顺时针，一个逆时针）。与角块三循环类似，我们的策略是将魔方视作两份：

    仍然是【X Y X’ Y’】格式，序列Y只影响图中的绿色层（两个需要翻色的角块都在这一层），而序列X将主要影响图中灰色部分，同时把绿色层的其中一个角块翻转。基本策略如下：

    ①使用序列X把A块原地翻转，同时保持F层其他块不受影响（三个例子均使用【R B’ R’ U’ B’ U】将UFR位置的角块原地逆时针翻转，但这并非唯一方法，例如【R' D' R D R' D' R】也可以，不过步数多了一些）。

    ②使用一步序列Y把B块移到B块的位置，这一步只动F层。

    ③做X’，翻转B块（X和X’分别使UFR位置的角块原地逆时针或顺时针翻转）。

    ④做Y’，把A块和B块移回本来的位置。

    PS：将两个角块同时原地顺/逆时针翻转是不可能的，但如果有三个角块的色向错误，一定都是原地顺时针或逆时针翻转。具体原因参见下一节“魔方的法则”。

基础技能部分到这里就结束了，浅聊一点个人思考。本节讲的共轭和转换机，虽然花了三千余字，但只是初学时不容易理解，熟练后应用并不困难；而前一节寥寥数语提纲掣领的筑块，我想才是最需要巧思的，这也是贯穿Heise法全程的思路。这就有点像CFOP的前两层、桥式的左右桥、Petrus的223，与结尾那些规则严明，甚至能完全公式化的步骤不同，筑块阶段是直接面对魔方的4.3×10^19种状态……

有时我不禁怀疑，Ryan Heise在教程前言强调的“零记忆”是否是一个悖论，又或者说真正的“零记忆”只存在于没有复原经验的魔方新手那里？因为不论是筑块还是转换机，要做到理解和灵活运用，“记忆”或者说“经验”都是必不可少的（登峰造极者参考Tymon Kolasiński只花5秒全预判F2L……）。再进一步讲，要做到“高效”地复原，不论是竞速还是追求短步数，只要经过反复练习，大脑都会习惯性记忆曾经用过的解法。正如单色底之于中立底色，思维固化总在无形中……

不纠结这个文字游戏了（瘫）Heise法的的确确是一套“不记公式”的解法。我们作为学习者，灵活运用才是关键～