本文默认读者知道LA基础知识，不再赘述。不清楚可自行查阅CV8169123

前言

        众所周知，LA模式中圆孔宝石不生效，只有方孔宝石才有效。若满足了方孔宝石的条件，则直接简单粗暴按比例加分，比如裸分100w，所有方孔宝石总的加成是2.5倍，那就直接变250w参与结算，非常简单粗暴。然而，面板值显示的加成数字是队伍所有方孔宝石加成叠加得到的总和，但实际加成却是所有宝石的叠乘。因此，如何使用总和来估算叠乘的数值，成了新的课题。

        上图面板显示的是无条件加分68000，fc加分1370000，50个P加分68000，三者总和1506000。如果同时满足这些条件，所有宝石加成的总和是每100w分，额外加成150.6w分，变250.6w，也就是乘2.5倍。然而，实际加成由于是叠乘，并不是叠加，因此会比2.5倍高许多，实际加成倍数为4.25倍。问题来了，我们如何根据面板给出的叠加的总和数值，来估算实际叠乘的加成倍数？已知加成倍率的总和，那他们的叠乘的最大和最小值应该是多少？

1.     变量定义与数学模型

        我们设第一个宝石的加成比例为x1，第二个为x2，以此类推到xn。n为队伍所有宝石的数目。比如，第一个4孔fc宝石的加成比例为8.3%，则x1=0.083。n∈[1, 72]，xn>0。如果队伍宝石插满，则n∈[18, 72]。

        我们设面板数值的总加成是t。则有：

        比如，面板数值总和是150.6w，则t=1.506（面板给的数值是按100w作基准的，因此要除以100w得到t）。也就是说，这队所有宝石加成的总和是1.506。我们本文假设队伍所有的宝石都能生效，不能生效的宝石不纳入t的计算。

        我们记所有宝石加成比例的叠乘，也就是实际加成倍数为s。则有：

        我们需要做的就是，在t为给定的定值的情况下，求s的取值范围：

2.     最小值

        我们先看s的最小值。存在广义伯努利不等式：

        因此，我们直接可以一步得出s的最小值：

3.     最大值

        我们继续看s的最大值。存在均值不等式：

        我们只看Gn和An，Gn≤An等价于：

        所以，有：

        于是我们得到了最大值，即：

        此外，由于后者在(0,+∞)上是增函数且有上界（证明不做展开，当本次思考题吧）；因此t相同，n越多，实际叠乘得到的加成越高，但存在上限。即，面板数值相同时，宝石数目越多，实际叠乘得到的加成总倍数越大。存在以下极限：

        因此，有：

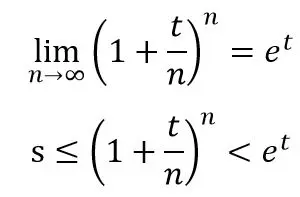
        把以上综合起来，得到：

        如果准确知道n的数目的话，最小值可以继续细化，因为每个宝石是有最小加成的（N-0.1%）。先把t拆成1个最大面值的4孔宝石和其他最小面值的宝石，然后再手工叠乘起来，计算很繁琐。提出这个最大最小值的意义在于快速估算，繁琐就没有意义了，所以不展开。

4.     简单的估算方法

        队伍宝石只上了个别（使用槽数＜16）时，直接用1+t预估：

        直接用1+t预估还有一个原因，因为宝石少的时候，t本身就很低，e^t和t+1差距极小，不管用哪个预估都行。

        队伍宝石插满时，n至少18起步，往往30以上（复合宝石类内也是叠乘），直接用e^t预估：

        如果不多不少，上了小半队，而且不愿意一个个数的话，可以取个加权平均（最大值算3份，最小值算1份，也就是3/4*e^t+1/4*(1+t)）：

        可见，预估公式准确度还是可以的。也可以反过来算，比如初步估计队伍需要总倍数为4倍才能通关，则如果宝石插满，需要每个ur平均加成不低于In(4)/72*4=7.70%，每个ssr平均加成不低于In(4)/72*3=5.78%。但注意，实际加成最好再略高一些，因为这个用e来估算用的是极限，实际取不到的。

5.     展望

        从联动塔开始，la加成已经开始崩了，新宝石直接淘汰了所有旧的。由于叠乘的性质，即使单个宝石的增幅不大，但总增幅却是e的指数函数，增幅非常可怕。如果宝石进一步数值膨胀，这个系统要被玩坏。目前最高单个4孔UR15.3%，15.7倍；当每个ur加成数值到18%时25倍，20%时37倍，22%时52倍，25%时90倍。到时候谁能过la，完全取决于能不能搞到当期最新宝石，队伍本身将不再重要。当然，不排除bxm可能等膨胀差不多了再推出一个新的换皮la，让旧la宝石全部失效，从头开始……

本期就这些内容，欢迎评论探讨~