郑涛（Tao Steven Zheng）著

【问题】

波斯天文学家、数学家阿尔·卡西（Jamshid al-Kashi，1380 - 1429）在《论弦与正弦》中利用三倍角正弦公式（triple-angle sine formula）来计算出精确到小数点后18数位的 值（）。使用 和 来证明 。

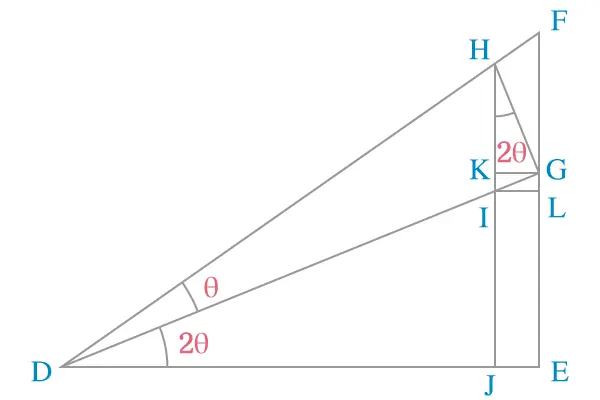
【题解】

首先写下正弦和角公式（angle-sum formula for sine） ，然后代入 。

已知正弦和余弦的二倍角公式（double-sum formulas）是

所以

由于 ，得

因此，

【附加问题】

证明：。