大学物理（原子物理学）知识梳理与例题选讲：§01 原子的卢瑟福模型

卢瑟福之前的原子物理

# 阴极射线：空气分子的电离

在两极中充入稀薄的空气下，发生微弱的电流，有些情况会发光

考虑荷质比

## 荷质比的测定

• 利用速度选择器（电场+磁场）（汤姆孙）

• 油滴实验——密利根

发现电荷具有“量子化”

• 枣糕模型

散射实验与卢瑟福模型

# 散射

• 场强分布与动能

求解动量p与动量变化量Δp的关系（即求散射夹角θ）

## 半定量模型

假设：

• 不考虑电子之间的相互作用
• 因原子外部的场强E与距离r^2反比，故不考虑原子外界的作用
• 原子核质量较大，不考虑原子核的动量变化

• 盖格-马斯顿实验

# 卢瑟福的思考

核式模型

## 卢瑟福模型存在的问题

• 稳定性问题

• 同一性：同一元素的性质相同，而卢瑟福模型的电子排布为任意轨道
• 再生性：原子在经历一些作用后可恢复的状态
• 线状光谱

优点：

较好的解释散射问题

卢瑟福公式与薄靶散射问题

# 求解散射角的问题

## 概念

靶原子M：被冲击的例子

瞄准距b：靶原子M到入射粒子速度v方向的形成射线的距离b

• 散射角θ：在库仑力的作用下（有心力）其为双曲线【力学：角动量-万有引力】的渐近线形成的夹角

## 问题的假定

## 运动轨迹

两体问题：简化质量

角动量守恒与能量守恒

推导轨迹方程

在散射中的轨迹

## 求解散射角

• 思路：积分 --> 求解最近点与靶点的直线与渐近线的夹角φ

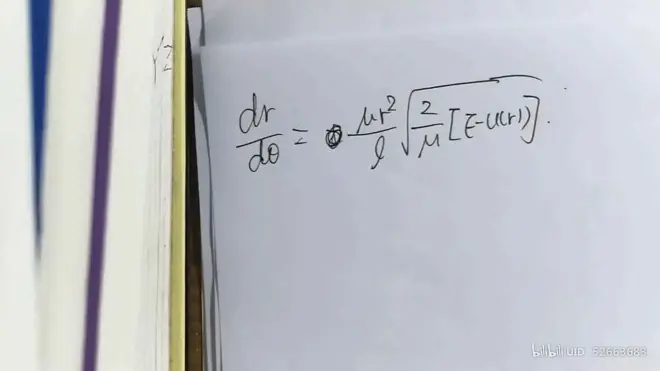
计算

夹角φ的表达式

• 求解最近点r_min

半偏转角φ的结果

散射角θ(b)【瞄准距离b】

存在可测量的问题：瞄准距b无法测量

# 散射截面

散射截面微元dσ为

回顾立体角的定义

散射截面的立体角dΩ

由散射微元面dσ

最终可得卢瑟福公式

定义量——单位立体角对应的散射截面

## 散射概率

求解入射粒子群以θ~θ+dθ角范围内散射的概率dp(θ）

散射概率dp(θ)表示式

可得

散射频率N

## 例题：卢瑟福公式

### 例1：变化动能

d已知：动能E、质量m、瞄准距b，重核质量Z

动量p的表示式

• 求解变化的动量Δp

由上代入可得

• 当瞄准距b为定值，动能E可变时，动量变化值Δp的最大值

由基本不等式可得

此时动能E为

此时可知——散射角θ为

### 例2：薄板散射

• 使用概率比值

• 使用散射截面之比

### 两板叠加问题