第 53 讲：含有隐性视角的致命结构

2021-09-01 00:32 作者:SunnieShine 0人读过 | 我要投稿

实际上我们已经学会了大部分的致命结构了，不过依然有一些结构论证起来非常复杂，而通过之前的方式依然是很难找到切入点，甚至无法找到切入点。下面将选取一部分这样的形式作为讲解的内容。

致命结构除了之前的逻辑以外，我们还可以为其嵌入隐性视角，这样的结构称为隐性致命结构（Hidden Deadly Pattern）。这种结构看起来复杂，证明起来，更复杂。

Part 1 带有隐性视角的致命结构？

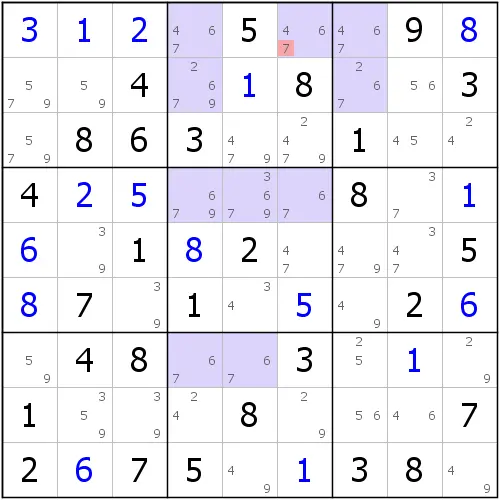
如图所示，这个结构是一个致命结构，不过它有点奇怪的是，以往我们理解致命结构都是通过显性的层面来思考的，不过这一次我们需要隐性来理解了。可以发现到的是，r35的所有填入8和9的位置只有r35c789，那么r3里放下8和9的地方就只有r3c789里选其中两个单元格；同理，r5也是一样。

如果r9里放下8和9的位置也只能是在同r35的对应位置r9c789里的话，会发生什么现象？显然，8在里面必须有三处要放8，而9也是。不管怎么放8和9，你都会发现，8和9的放置最终都会形成唯一矩形或唯一环的致命形式，即8和9可以交换的局面。所以，r9c789里不能有任意一处可以放9的地方，所以r9c789 <> 9。

这一则示例我们可以看到，如果r9c789是r9里唯一能放下9的三处地方的话，那么不管8和9的放置方式如何，最终都将致命，所以这一种使用方式非常的神奇和新颖。

Part 2 又是一则带有一点隐性视角示例

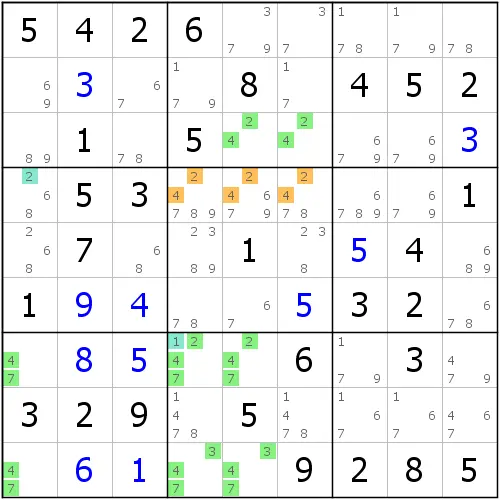
这个例子我们先来说说结论。如左图所示，如果r4c1(2)和r7c4(1)同时去掉的话，我们画出来的这些单元格将会组成一个致命形式，于是我们能够找到一条链，并使用刚才的强关系，得到一条不连续环，并得到删数。

那么，这个致命结构是如何产生的呢？我们可以将这个结构的构型提取出来。

如图所示。我们可以看到，这个结构的下方r79c145只有2、3、7、9，我们完全可以使用传递性，将这些单元格传递变为一个2、4的数对。

别急，我知道你肯定有一处疑问。r6c45如果是2和4的话，岂不是影响到r4c456的2和4的填数了？看起来确实是，不过我们需要注意的是，这里宫内的2和4实际上和它是不构成直接的影响的关系的，因为r6c45的这个2和4实际上并不一定在这个位置，这只是我们在传递的时候，为了固定数字，并持续向下推导时选择好的一处地方而已，所以我们不能直接说这个2和4是可以影响到r4的三处2和4的单元格的。

实际上在之前的示例里，我们完全也可以把一些传递后的数对或者数组结构安放在看似会冲突的地方上去，这一点的原因和上面我解释这里2和4的冲突的原因是一样的，因为传递后产生的数对或数组结构的位置本身就是不固定的，固定下来也仅仅是为了能够更好地向下推导其逻辑。但是固定下来也不代表它一定就在这里，因为我们只是拿出了构型来推理，可以很明显地发现，原盘面多数情况下，在我们传递好的位置上是有确定值的，所以实际上就安放传递后的数组结构的位置这一点来看，实际上只要能和原结构保持致命形式的出现，放在哪里其实并没有什么关系，只是要注意，不要把传递的结构和原结构拿来混淆，否则有时候完全区分不开，导致无法继续推导，或者错误地使用了该传递性。

以前的示例里，我们可以发现的是，传递后的结构的位置都是放在一些完全不受影响的地方，这一点就是为了避免错误地理解我们此处提到的可能产生混淆的内容。

接着我们就可以使用刚才第一则示例的逻辑了。我们不论怎么安放r4的2和4的位置，由于结构2和4在r36的2和4的位置是固定的，所以这三处2和4的安放只会使得这些位置要么形成UR的致命形式，要么形成UL的致命形式。所以，整个结构实际上是致命的。因此，最初得到的强关系得以论证，即我们原定要消失的数字并不可以同时被去掉。

Part 3 综合示例

最后我们来看一则比较麻烦的示例。如图所示，这是一个致命结构，如果r6c8(4)去掉的话，它将形成致命形式。现在我们来证明思考一下这是为什么。

我们先把结构抽象出来。

如图所示。注意，b14里的5和6还有7和8是隐性的视角，仅这些单元格可以填入，并非是提取过程之中出现错误。

首先，我们观察到，b5里的数字是1、5、6、7，所以我们完全可以在它的两侧补上相应的结构，使之形成一个合格的四数探长致命结构的致命形式，为了题目更简单，我们在结构靠下方补上5、6数对，而右侧补上1、7数对，变为下面这个图里展示的这样。

接着，我们可以看到，r56c89是1、7、8，显然可以为左侧补充7、8使之构成拓展矩形的致命形式，而5、6可以发现可以补充5、6构成唯一环形式，所以我们补充上匹配的5、6数对和7、8数对，于是结构变为这样。

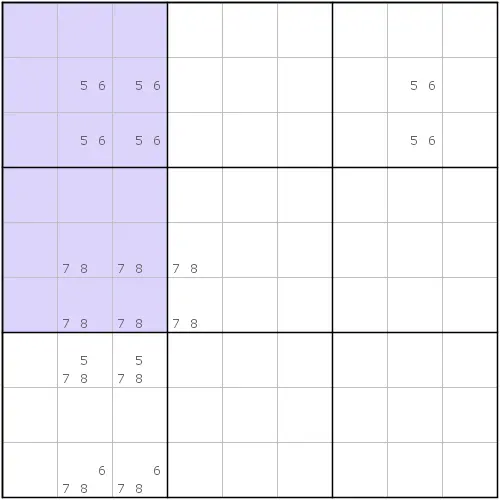
如图所示。可以发现，此时结构就比较清晰了。我们这样去思考这个问题。由于此时r23c8(56)是我们传递的结果，而r56c4(78)也是。虽然它们的位置并非必须要放在这里，但由于相对位置是不能发生改变的，即要保证原始传递过来的部分是可以还原回去形成致命形式的，所以现在的这个部分的相对位置是不允许发生任何的改变的。这也就是说，r23c8(56)完全可以调整到r23c4(56)来，甚至是r23c1(56)来，但必须是r23里同列的单元格；同理，r56c4(78)也是这样的道理。

那么基于这一点，我们注意b1，发现b1里的5和6此时就只能斜着放了。因为横着放5和6会导致r23c8(56)传递出来的单元格的其一无法填数，导致出错；而竖着填就会立马配合r23c8(56)形成关于5、6的致命形式，所以数字5、6此时在b1里只能斜着放进去。同理；b4里的7、8也是一样的道理。

那么，既然只能斜着放，那么为什么我们不能视作唯一环的一部分呢？拿r23c8(56)来说，配合b1里5、6斜着放的特性，只要c23里出现同行的5、6数对，就算是形成UL的致命形式了，那么我们可以利用这一点，把这个隐性的视角通过传递性，转化到c23上某一同行的两个单元格上；同理，7和8对于b4也是一样，所以我们传递的最终版本变为了这样。