真空迭代制导定点

2023-08-04 14:52 作者:咆哮鼠啊啊啊 0人读过 | 我要投稿

前言

介绍一下我多次探索迭代制导，终于成功复现的一个真空单级着陆的方案。这篇文章不会详细介绍具体的数学物理原理，主要分享一下制导的计算流程，不保证正确，如果时间和水平允许也许会写一个简单的原理分析，欢迎指正

物理量

常量（初次运行时读取/设定/计算）

$%5Cmu$ ：单位 $%5Crm%7Bm%5E3%2Fs%5E2%7D$ ，星球引力常量，等于万有引力常数乘星球质量（ $%5Cmu%3DGM$ ）

$T$ ：单位 $%5Crm%7BN%7D$ ，引擎最大节流阀推力

$V_e$ ：单位 $%5Crm%7Bm%2Fs%7D$ ，引擎喷气速度，数值等于比冲秒数乘9.81

$%5Cdot%7Bm%7D$ ：单位 $%5Crm%7Bkg%2Fs%7D$ ，引擎最大节流阀的质量消耗速率（ $%5Cdot%7Bm%7D%3DT%2FV_e$ ）

$%5Cvec%7BR%7D_f%2CX_f%2CY_f%2CZ_f$ ：单位 $%5Crm%7Bm%7D$ ，设定的制导终端位置矢量和三分量

$%5Cvec%7BV%7D_f%2CV_%7Bfx%7D%2CV_%7Bfy%7D%2CV_%7Bfz%7D$ ：单位 $%5Crm%7Bm%2Fs%7D$ ，设定的制导终端速度矢量和三分量

$t_p$ ：单位 $%5Crm%7Bs%7D$ ，制导周期，每个制导周期开始时刷新一次制导参数，通常是迭代周期 $dt$ 的整数倍

$dt$ ：单位 $%5Crm%7Bs%7D$ ，迭代周期，每个迭代周期刷新一次控制量

状态参数（每个迭代周期读取一次）

$m$ ：单位 $%5Crm%7Bkg%7D$ ，瞬时质量

$%5Cvec%7BR%7D%2CX%2CY%2CZ$ ：单位 $%5Crm%7Bm%7D$ ，瞬时位置矢量和三分量

$%5Cvec%7BV%7D%2CV_%7Bx%7D%2CV_%7By%7D%2CV_%7Bz%7D$ ：单位 $%5Crm%7Bm%2Fs%7D$ ，瞬时速度矢量和三分量

每个迭代周期更新一次的参数

中间参数：

$t_%7Bgo%7D$ ：总剩余飞行时间

$t$ ：制导周期内的已飞行时间

$%5Cvec%7Bg%7D%2C%5Cvec%7Bg%7D_f$ ：当前、终端引力加速度矢量和三分量（ $%5Cvec%7Bg%7D%3D-%5Cfrac%7B%5Cmu%5Cvec%7BR%7D%7D%7B%7C%7C%5Cvec%7BR%7D%7C%7C%5E3%7D$ ， $%5Cvec%7Bg%7D_f$ 同理）

$%5Cvec%7Bg%7D_m%2Cg_%7Bmx%7D%2Cg_%7Bmy%7D%2Cg_%7Bmz%7D$ ：平均引力加速度矢量和三分量（ $%5Cvec%7Bg%7D_m%3D%5Cfrac%7B1%7D%7B2%7D(%5Cvec%7Bg%7D_f%2B%5Cvec%7Bg%7D)$ ）

$%5CDelta%20%5Cvec%7BV%7D%2C%5CDelta%20V_x%2C%5CDelta%20V_y%2C%5CDelta%20V_z$ ：推力产生的总速度增量矢量和三分量

$%5Cvec%7Bu%7D%2Cu_x%2Cu_y%2Cu_z$ ：引擎产生的加速度矢量和三分量

控制参数：

$%5Cvarphi%2C%5Cpsi$ ：姿态角

$k$ ：节流阀

每个制导周期更新一次的参数

中间参数：

$F0%2CF1%2CF2%2CF3$ ：推力积分

制导参数：

$k_%7B%5Cvarphi1%7D%2Ck_%7B%5Cvarphi2%7D%2Ck_%7B%5Cpsi1%7D%2Ck_%7B%5Cpsi2%7D$ ：制导率参数

$%5Cvarphi_v%2C%5Cpsi_v$ ：仅满足速度约束的姿态角

$%5Cvarphi_c%2C%5Cpsi_c$ ：仅满足速度约束和YZ方向位置约束的姿态角

坐标系与姿态角

这里默认着陆点在轨道平面内。坐标系原点O在星球中心，OY指向终端位置；OX在轨道平面垂直于OY，与飞船速度同向；OZ垂直轨道平面

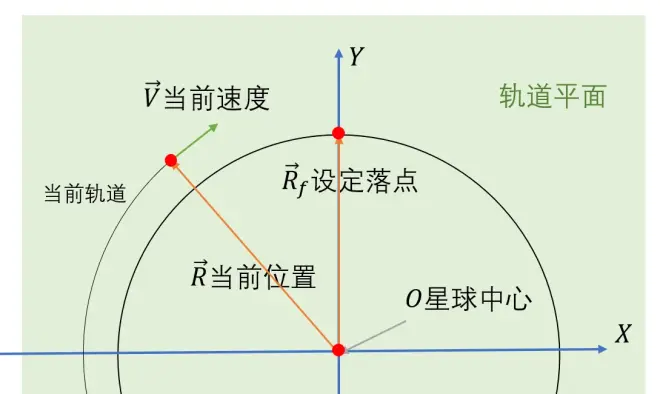
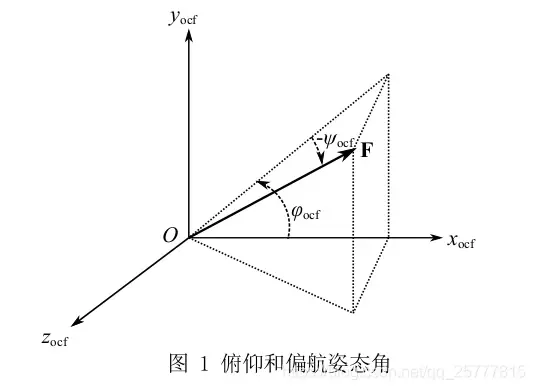
这里默认火箭受到的推力方向和火箭指向方向相同。姿态角 $%5Cpsi$ 是火箭方向矢量与其在XY平面的投影的夹角，从XY平面向Z轴正半轴方向为负；姿态角 $%5Cvarphi$ 是火箭方向矢量在XY平面的投影与X轴正半轴的夹角，从X轴正半轴向Y轴正半轴方向为正。左右手系都可以用这套规则。 $%5Cvarphi%2C%5Cpsi$ 与习惯意义上的俯仰和偏航有区别，注意区分

制导流程

一、调整轨道，让轨道足够低，且轨道平面离着陆点足够近，选择合适的点火时机

二、初始化全部常量（星体参数、引擎参数、着陆点参数），进入迭代循环

三、迭代

1. 读取火箭状态量参数（位置、速度、质量）

2. 估计全程平均引力加速度 $%5Cvec%7Bg%7D_m%3D%5Cfrac%7B1%7D%7B2%7D(%5Cvec%7Bg%7D_f%2B%5Cvec%7Bg%7D)$

3. 预估一个 $t_%7Bgo%7D$ ，使用以下两个公式迭代至收敛，得到剩余飞行时间 $t_%7Bgo%7D$ 和推力产生的总速度增量矢量 $%5CDelta%20%5Cvec%7BV%7D$

$%5Cbegin%7Balign%7D%0A%5CDelta%5Cvec%7BV%7D%20%26%3D%20%5Cvec%7BV%7D_f-%5Cvec%7BV%7D-%5Cvec%7Bg%7D_mt_%7Bgo%7D%20%5C%5C%0At_%7Bgo%7D%20%26%3D%20%5Cfrac%7Bm%7D%7B%5Cdot%7Bm%7D%7D%5B1-%5Cexp(-%5Cfrac%7B%7C%7C%5CDelta%20%5Cvec%7BV%7D%7C%7C%7D%7BV_e%7D)%5D%0A%5Cend%7Balign%7D$

4. 根据 $t_%7Bgo%7D$ 、速度误差 $%5CDelta%5Cvec%7BV%7D$ 、位置误差 $%5Cvec%7BR%7D_f-%5Cvec%7BR%7D$ 判断是否结束迭代

5. 如果是新制导周期内的第一次迭代，刷新制导参数，否则跳过以下刷新制导参数的步骤，使用所在制导周期第一次迭代计算的制导参数

5.1 计算推力积分

$%5Cbegin%7Balign%7D%0AF0%20%26%3D%20V_e%20%5Cln%20%5Cfrac%7B%5Ctau%7D%7B%5Ctau-t_%7Bgo%7D%7D%20%5C%5C%0AF1%20%26%3D%20%5Ctau%20F_0%20-%20V_e%20t_%7Bgo%7D%20%5C%5C%0AF2%20%26%3D%20F0%20t_%7Bgo%7D%20-%20F1%20%5C%5C%0AF3%20%26%3D%20F2%20%5Ctau%20-%20%5Cfrac%7B1%7D%7B2%7DV_e%20t_%7Bgo%7D%5E2%0A%5Cend%7Balign%7D$

5.2 计算 $%5Cvarphi_v%2C%5Cpsi_v$

$%5Cbegin%7Balign%7D%0A%5Cvarphi_v%20%26%3D%20%5Carctan%5Cfrac%7B%5CDelta%20V_y%7D%7B%5CDelta%20V_x%7D%20%5C%5C%0A%5Cpsi_v%20%26%3D%20-%5Carcsin%5Cfrac%7B%5CDelta%20V_z%7D%7B%7C%7C%5CDelta%5Cvec%7BV%7D%7C%7C%7D%0A%5Cend%7Balign%7D$

5.3 计算 $k_%7B%5Cvarphi1%7D%2Ck_%7B%5Cvarphi2%7D%2Ck_%7B%5Cpsi1%7D%2Ck_%7B%5Cpsi2%7D$

$%5Cbegin%7Balign%7D%0Ak_%7B%5Cvarphi1%7D%20%26%3D%20%5Cfrac%7BY_f-F2%5Csin(%5Cvarphi_v)%5Ccos(%5Cpsi_v)-1%2F2g_%7Bmy%7Dt_%7Bgo%7D%5E2-V_yt_%7Bgo%7D-Y%7D%7B(-F2%2B%5Cfrac%7BF3F0%7D%7BF1%7D)%5Ccos(%5Cvarphi_v)%7D%20%5C%5C%0Ak_%7B%5Cvarphi2%7D%20%26%3D%20k_%7B%5Cvarphi1%7D%5Cfrac%7BF0%7D%7BF1%7D%20%5C%5C%0Ak_%7B%5Cpsi1%7D%20%26%3D%20%5Cfrac%7BZ_f%2BF2%5Csin(%5Cpsi_v)-1%2F2g_%7Bmz%7Dt_%7Bgo%7D%5E2-V_zt_%7Bgo%7D-Z%7D%7B(F2-%5Cfrac%7BF3F0%7D%7BF1%7D)%5Ccos(%5Cpsi_v)%7D%20%5C%5C%0Ak_%7B%5Cpsi2%7D%20%26%3D%20k_%7B%5Cpsi1%7D%5Cfrac%7BF0%7D%7BF1%7D%0A%5Cend%7Balign%7D$

6. 计算 $%5Cvarphi_c%2C%5Cpsi_c$

$%5Cbegin%7Balign%7D%0A%5Cvarphi_c%20%3D%20%5Cvarphi_v-k_%7B%5Cvarphi1%7D%2Bk_%7B%5Cvarphi2%7Dt%20%5C%5C%0A%5Cpsi_c%20%3D%20%5Cpsi_v-k_%7B%5Cpsi1%7D%2Bk_%7B%5Cpsi2%7Dt%0A%5Cend%7Balign%7D$

7. 计算 $%5Cvec%7Bu%7D$

$%5Cbegin%7Balign%7D%0Au_x%20%26%3D%202(X_f-X-V_%7Bx%7Dt_%7Bgo%7D-%5Cfrac%7B1%7D%7B2%7Dg_%7Bmx%7Dt_%7Bgo%7D%5E2)%2Ft_%7Bgo%7D%5E2%20%5C%5C%0Au_y%20%26%20%3D%5Cfrac%7BT%7D%7Bm%7D%5Csin(%5Cvarphi_c)%5Ccos(%5Cpsi_c)%20%5C%5C%20%0Au_z%20%26%3D%20-%5Cfrac%7BT%7D%7Bm%7D%5Csin(%5Cpsi_c)%0A%5Cend%7Balign%7D$

8. 计算控制参数

$%5Cbegin%7Balign%7D%0A%5Cvarphi%20%26%3D%20%5Carctan%5Cfrac%7Bu_y%7D%7Bu_x%7D%20%5C%5C%0A%5Cpsi%20%26%3D%20-%5Carcsin%5Cfrac%7Bu_z%7D%7B%7C%7C%5Cvec%7Bu%7D%7C%7C%7D%20%5C%5C%0Ak%20%26%3D%20%5Cfrac%7Bm%7C%7C%5Cvec%7Bu%7D%7C%7C%7D%7BT%7D%0A%5Cend%7Balign%7D$

四、结束制导进入下一阶段

已知问题

这里没有考虑自转，常量中的落点信息应该设定落点的经纬度和海拔高度，在估算 $t_%7Bgo%7D$ 之后计算落点坐标，如有必要还需要根据新计算的落点坐标重新建立坐标系

X方向使用匀加速模型控制落点的X位置，很大程度上破坏了最优化问题求解得到的好结果

理论上 $k_%7B%5Cvarphi1%7D%2Ck_%7B%5Cvarphi2%7D%2Ck_%7B%5Cpsi1%7D%2Ck_%7B%5Cpsi2%7D$ 都是rad或rad/s单位的小量，但如果轨道太高或者点火时间不在窗口期，可能出现 $k_%7B%5Cvarphi1%7D%2Ck_%7B%5Cpsi1%7D$ 比 $%5Cpi$ 还大的情况