下面我们来阐述一些其它技巧跟网结构的关联。

Part 1 鱼直观的原理

第一个我们需要讲到的内容就是鱼结构。实际上，鱼结构的直观我们已经在很前面的内容里说过了，但我们并没有证明之。现在我们尝试把之前的理论进行证明，实际上，之前的理论我们都是通过网结构才能得到证明。

1-1 先来回顾一下

我们先回顾一下推导过程。

如下方左图所示，我们尝试在结构里找到m * n的矩形区域，需要满足如下的要求：

• 矩形区域涉及的结构里不能含有我们需要找的鱼所涉及的数字的确定值；

• 矩形区域所处的所有行列区域上都不允许含有我们需要找的鱼所涉及的数字的确定值；

• 设矩形区域以外，鱼涉及的数字的确定值总个数为k，而矩形涉及大小为m * n，需要满足m + n + k = 9。

这个示例就满足上述的三点要求：矩形区域里没有5，矩形区域所在行列上的任何一点也都没有5，而在区域外的其它部分含有一个5（k = 1），且满足矩形区域大小（4 * 4）代入的公式：4 + 4 + 1 = 9。所以这样就有鱼结构的存在了。而且实际上，我们确实能找到鱼结构，如右图所示。

下面我们来证明一下这个内容。

1-2 证明

我们认为下方图上这样的结构就有鱼结构的存在了。

这是一则框架图，并不是一个唯一解的题目。不过可以从结构上发现，它确实存在鱼。那么我们想用直观视角叙述的内容是什么呢？

这个图上有一个关于数字4的三阶的标准鱼（也称三链列和剑鱼）。

我们需要记住如下的术语和公式。

术语：

• 域内：直观标准鱼结构需要有一个“阵列”的构造出现，例如图上的r247c1468这样12个单元格。这么12格我们称为区域内，简称域内。

• 域内确定值（简称域内数）：在域内的该数的确定值集合，比如图上的域内不包含任何该数字，所以图上并没有域内数。

• 架子：区域内单元格横向或纵向涉及的所有区域，r2、r4、r7、c1、c4、c6、c8这7个区域的所有单元格直接称为架子。

• 域外：盘面除了架子外的剩余单元格。

• 域外确定值（简称域外数）：在域外的该数确定值集合，比如图上的r1c9(4)和r5c7(4)统称为区域外提示数。

• 域外内净次数（Net Extraterritorial and Intraterritorial Numbers，简称NAIN）：该数值等于区域外提示数个数减去区域内该数总个数得到。比如该图里，区域外有2个4，区域内则没有4（0个4），则域外内净次数等于2 - 0 = 2。

公式：

• 如果设架子一共由n个区域构成，且域内包含k个要找的鱼涉及的这个数，区域外提示数一共有m个，则当且仅当NAIN值等于“9 - 架子区域数”的时候，才有标准鱼的出现（或带鱼鳍的标准鱼、带链的鱼鳍标准鱼等等），且鱼的定义域产生于架子上，而删除域产生于域外。

我们先把公式用数学语言描述一下，然后以便后面的理解和对照。

域外内净次数（NAIN） = 9 - 架子区域数（n）

我们为了证明简单一些，使用移项和拆解后的公式：

域外数个数（m） - 域内数个数（k） + 架子区域数（n） = 9

由于n是架子区域总数，我们拆解为两个分量a和b（分别表示横向架子区域数和纵向架子区域数），这样就可以表示和体现出架子是涉及a行b列的。那么一定有

横向架子区域数（a） + 纵向架子区域数（b） = n

而

域内单元格总数 = a * b

我们现在来数一下域外单元格总个数。因为架子区域是a行b列的，所以域外单元格总数应当是

域外单元格总数 = (9 - a) * (9 - b)

而架子涉及的是a * b个单元格，所以可以从式子上得到，架子外单元格总数就比架子本身要多出来(9 - a) * (9 - b) - a * b个单元格。先把这个结论记下来，一会儿会用到，现在我们切换一下内容，来看结构。

如图所示，可以从图上看出，所有的橙色单元格就是所有的域外单元格了。

现在，橙色单元格加上淡绿色单元格，刚好凑齐c23579五列，因为是五列，所以填数一定是数字1到9各有5个的（每一列都有1到9各一个，所以五列就各5个）。

再横着看。紫色单元格就是我们所有的域内单元格了。紫色单元格加上淡绿色的单元格，刚好凑齐三行，所以填数一定是1到9各有3个的，即：

橙色单元格 + 淡绿色单元格 = 5套1到9

紫色单元格 + 淡绿色单元格 = 3套1到9

我们针对于这两个式子作减法运算：

橙色单元格 - 紫色单元格 = 2套1到9

再移项。

橙色单元格 = 2套1到9 + 紫色单元格

这样就意味着，橙色包含所有紫色单元格的所有填数，还外带两套完整的1到9序列。

例如我们现在来看图上的数字4。

域内（紫色）单元格是不存在数字4的（即此时k = 0），而从式子里可以看到，域外（橙色）单元格具有两套1到9和紫色单元格的所有数字，而紫色里又没有4，那么只能说明2套1到9里的2个4将是橙色单元格里所有的4了。换句话说，橙色就不应当再出现其余任何的4。

刚才只是举例说明我想表达的意思，现在来推广到一般化的情况。域外单元格（橙色）的总数就比域内（紫色）单元格的总数本身要多出来(9 - a) * (9 - b) - a * b个单元格，那么域外单元格的填数比域内的填数会多出来多少套完整的1到9呢？显然就是用这个数除以9即可，则有：

并最终我们得到了一个公式：9 - n，即橙色比紫色多出(9 - n)套1到9，n还记得指代的是什么吗？n就是架子区域数了（因为a和b分别代指的是横向架子区域数和纵向架子区域数，所以加起来就是总的架子区域数）。这意味着什么呢？如果架子不包含我们寻找的标准鱼结构所涉及的数字，而此时区域外单元格的部分（橙色）就包含(9 - n)套1到9，外加上架子内（紫色）的所有确定值。但如果紫色区域内不包含我们要找的数的话，那么数字就只可能出现在(9 - n)套1到9的这一项里。当(9 - n)恰好等于我们在区域外找到的这个数字的总个数时，区域外就不会再存在其余的这个数字了的填数位置了。

那么此时看下刚才“具象化”后的公式：

橙色单元格 + 淡绿色单元格 = 5套1到9

既然橙色（域外）里没有这个寻找的数字的容身之地，那么这个数就只可能出现在淡绿色单元格里。如果域内里没有我们费尽千辛万苦寻找的数字，而必须又得需要5个这个数，现在域外是不能再填这个数了（域外有2个了），而为了保证数字不出现违背数独规则的现象，还剩下3个这个数，它们就只可能出现在不会直接和提示数冲突的地方（即淡绿色格子里）。而又要保证行列上不要违背数独规则“重复”，那么数字就只能允许填入到它们应当放到的位置上。于是，标准鱼便形成了。

这一段如果不好理解，你可以对照图上来看。淡绿色的区域是3 * 5的区域，而提示数4的摆放位置一定是会和淡绿色具有同列的单元格的，毕竟这些4一定都在橙色单元格里，而橙色单元格又是和淡绿色单元格“正交的”，这就使得它就会连续排除两个在淡绿色填入4的位置。所以3 * 5的“5”就被压缩为了5 - 2 = 3。这个式子的“2”，指的就是这个4在域外的提示数的个数了（两个4）。那剩下来不就刚好3 * 3了吗？刚好我们从计算就得到了，必须要填3个，那么3 * 3的区域要填3个数，这不就已经满足了标准鱼的规则了吗？所以标准鱼一定会形成的原因我们就说清楚了。

所以说，只要出现最开始提到的公式，满足这个等式要求，那么就一定出现标准的鱼结构（当然，带鱼鳍的我们稍后会详细叙述其直观层面的推理逻辑）。

请注意，上面的证明使用的是k = 0的情况，当k <> 0的时候，证明方式完全一样，结论也成立，此处就不赘述了，但不代表公式的k可以被忽略。

另外，直观鱼的基本理论、术语词汇和证明均由中国数独玩家“辉煌背后的衰落”予以提出，部分术语有些晦涩，但作为证明也是必不可少的。

1-3 直观标准鱼视角的互补

在我们的推导和证明的过程之中，我们难免会遇到一些棘手但没有必要纠结的问题，比如鱼结构存在互补，但直观视角如何是思考互补的内容。实际上，这个答案很简单。我们来看一些示例。

如图所示，这个示例在我们之前已经出现过了。我们来看这个结构对应的两个互补的鱼结构。

如图所示，这个就是这个鱼结构对应的两个完全不同的候选数视角，不过一个是按列删数，一个则是按行删数。

我们再来看一则有关标准鳍鱼的示例。

如图所示，这也是之前的示例，我们可以发现，我们直接将整体的矩形对应的行换成列，就达到了互补的效果。当然，右图呈现的看起来是一个孪生鱼结构，似乎不完全是互补的。但实际上，我们针对于左图的结构，右图是它的互补的构型，这一点总是没有问题的。

所以鱼结构的直观视角里，互补仅仅是把矩形对应的行列区域（即架子）换一下而已。

1-4 标准鱼的观察

实际上，在前面已经提到了很多有关观察的内容了，不过没有说原理之前，理解起来是不那么容易的，这里我们再次阐述一下如何以直观视角观察鱼结构。

我们再次把提到的公式照搬过来（为了方便你看，所以我就复制一遍过来，就不用你往上翻了）：

NAIN = 9 - 架子区域数

为了凑公式，我们必须凑齐所有合适的数据才行。因为鱼是同数技巧，所以我们观察只需要从1到9挨个数一遍数字的位置即可。

如图所示，比如我们现在找到所有数字4的位置。接着，我们开始找域内。域内是我们随意找的，它可以包含提示数、填入数甚至是候选数单元格。只要我们保证这个数的相关信息带入到刚才的公式了，满足刚才的等式即可。

注意，即使候选数单元格包含该候选数，也不算作信息点带入到公式中。因为公式本身并不包含候选数是否包含的这一点的。

公式要想NAIN值等于9减去架子区域数，那么最好找的情况就是，找一个架子，使得域内没有这个数，且架子区域是7个的情况，这样NAIN = 2 - 0 = 2，就满足2 = 9 - 7的等式。所以我们需要找的架子规格必须是2 * 5、3 * 4等等情况（架子的架子区域数就是规格涉及的行和列个数的总和，即2 + 5 = 3 + 4 = 7，当然1 * 6也OK，不过，你可以思考下，如果真的存在1 * 6的，那会是个什么情况）。

现在我们找一个3 * 4的区域，如图所示：

恰好，域内不包含数字4，且域内刚好是3×4的“矩阵”，所以此时在架子区域里含有一个涉及4的标准鱼。实际上，鱼在这里：

这和我们的预期是完全一样的。

1-5 标准鳍鱼的观察

先来看这个例子。如图所示。我们从直观层面找到了这么一个东西。首先，数字7在域外有两个，所以为了保证和为9，我们选择找3 * 4的区域。

恰好，我们找到了该“矩阵”，NAIN = 2 - 0 = 2（注意，架子内是有一个候选数7的。这里是不是7我们是不确定的）。

此时讨论它是否是7。如果r9c6 = 7，则直接通过它所在行列宫执行排除删数即可；如果r9c6 <> 7，由于所有7已经被我们找完了，而且域内和这些7不同行列，所以公式也满足，标准鱼成立。于是删数存在于域外，故此时只需要去找到删数的具体宫（b8）和删除域的交集，即为删数。

而实际上，我们能找到关于7的鳍三链列，如图所示。

那么，鳍鱼的直观有什么特殊结论吗？其实是有的。试想一点，我们在直观层面是没有标注候选数的，而此时我们标注的架子是不区分行列“方向”的，它不像鱼会区分。所以，此时我们有一个结论是这样的：

我们使用这个图给大家解释下。由于7的位置不能确定行还是列上存在标准鱼，我们的结论是：以这个不知道7到底是否成立的单元格（即这里的r9c6）为“拐点”，所在宫内同行列的一共5个单元格（即r78c6、r9c45和r9c6五个单元格）里必有一个单元格是数字7。

当然，这个题上r78c6是被确定值占据了，因而没有7。我刚才的结论是推广到一般情况下的。而且，实际上这5个单元格叫做“关于r9c6的空矩形区域”，简称“空矩形”。

至于为什么会这样，说起来也很简单：因为直观层面不区分鱼的“方向”，所以既然删数成立，那么结构必然产生于架子里，而架子里一定会有鱼身的存在，所以不能保证具体在哪里，只能保证拐角的这个十字形状下的5个单元格（空矩形区域）里的这个数字必须有一个是为真的，这就是当观察直观版本的鳍鱼时，它所拥有的结论。

1-6 直观鱼的示例

下面阐述一些稍微难一些的直观鱼的示例。这些直观鱼的示例在之前都是没有说到的，因为在之前的内容里，我们并没有把技巧升华到这个难度。

以下的例子均和上面的逻辑完全一样，所以这里不再细述其逻辑。如果需要介绍，下面还是会有注释文字的。

示例1：标准鱼

示例2：孪生鱼

横着看，前面两个图是鳍鱼的第一种看法；后面两个图是鳍鱼的第二种看法，因为它们共用大部分域内单元格，而且从题上可以看出，它们使用了相同的鱼身，所以是孪生的鱼结构。

示例3：鱼和环的交织

这个需要解释下为什么。看第一个图，如果两个4同假，则域内不存在4的任何确定值，算上域外的提示数4，NAIN = 3 - 0 = 3，且此时恰好满足等式，即产生关于4的鳍鱼结构（这里不能说是鱼，因为r8c8的4是不知道是否存在的）。

刚才鳍鱼最后得到一个结论：十字形状的五个单元格里必须有一个4为真。但是观察这样的5个单元格（r789c8和r8c79），能填入4的位置仅剩下十字架的中间这一个单元格r8c8了，所以当r5c3 <> 4的时候，必须得有r8c8 = 4的结论。因而强关系成立。

而右图的6的强关系则是另外一种情况。因为域外有4个6的确定值了，所以此时看这个结构已经不成立了。不过……此时因为r8c8 = 4的关系，r8c8 <> 6也是事实。如果此时r5c3 = 6的话，会怎么样呢？

从原理上推进逻辑，如果域内有这个数，那么此时k = 1，根据公式要得到9，域外就必须有4个。确实盘面“履行了诺言”，出现了4个确定值6。那么此时鱼是成立的，因而r5c3=6是应当成立的；否则如果r5c3没有6，从原理上推进推理过程，6将放不满架子该放的总个数，于是便产生了矛盾（此处就自己推一下，我就不再作图说明了）。

总之，链写法如下：

这个链构成了环，并且成立。

此时留下一个问题：这环除了能删除基本的删数外，还有一些删数客观存在，你知道在哪里吗？

示例4：鱼和直推UR

如图所示，因为推导逻辑顺序不好标注到图上，所以没有箭头。现在我们用文本进行叙述。

我们假设r1c3 = 1，此时应当有r26c3 <> 1，且r6c3 = 6的结论。针对于r26c3 <> 1，它是架子上的单元格，如果两处都没有1，所以架子没有1，此时公式里的NAIN = 3 -0 = 3，于是恰好满足公式，所以删除域的1应当都可以被去掉，所以图中标注青色的数字1都是此时可以删除的数字。

接着，当这些1去掉后，结合刚才r6c3=6的结论，我们可以确定，b4里只有一处可以填1，即r6c1 = 1。然后根据直推UR的逻辑，r12c3由于r6c3 = 6的关系，这两个单元格也都不能填6。所以b1里填6的位置只有一处可填：r1c2 = 6。

此时，结合刚才的所有步骤，我们得到r1c2 = 6、r1c3 = 1、r6c2 = 1、r6c3 = 6，此时形成UR的致命形式，所以矛盾。所以最初的假设（r1c3 = 1）为假，即r1c3 <> 1，为该题结论。

示例5：另外一个环

如图所示，链表示如下：

首先我们来简单说一下。假设r9c5 <> 6了，则鳍鱼立马就形成了，还记得我刚才的逻辑吗？十字形状的5个单元格里必须得有一个6，所以此时r46c5和r4c4里必须出一个6。所以，r9c5(6) = {r46c5, r4c4}(6)强关系成立。接着，由于三格有一个6，所以r5c46不能填6。注意到ALS区域r5c46，所以r5c46(6)=r5c4(4)成立。后面就是基本逻辑了。

形成环后，删数逻辑就不用我一个一个说了。此时请注意ALS的删数比较特殊，2也可以删掉。

1-7 总结

本文介绍了直观鱼的基本公式，以及公式的证明。公式如下：

NAIN = 9 - 架子区域数

当满足该公式的时候，题目必然存在标准鱼结构。而这样的观察视角对于出题层面和解题层面都具有很大的帮助。

对于鳍鱼，还存在一个结论：如果架子存在没有确定的空单元格，且该单元格的候选数包含我们需要寻找的标准鱼所涉及的数字，则鳍鱼成立（前提是必须要满足公式再来谈这一点哈），以这个单元格为“拐角”，向该宫以行列方向延伸的十字形状的5个单元格里，必须有一个格填入的是这个数。

1-8 宫内鱼的直观

下面我们拿出简短的几句话内容来阐述一下，宫内鱼和交叉鱼的直观。

在我们之前直观的视角里，我们只要能够找到一个矩形区域的结构，便可得到存在鱼结构的结论，但具体在哪里我们并不知道。不过我们在证明的时候，并没有直接说明它的存在必须是什么形式出现。所以宫内鱼和交叉鱼也是可能在直观的视角里找到的。

但是，实际上，我们在找这样的结构的时候，肯定会遇到一定的问题，因为结构并不可能是以一种纯直观的构型出现展示在题目上，因为形状的关系，我们不论如何去放置这些确定值，都不可能立马可以形成一个宫内鱼和交叉鱼的构型。所以一般意义上，宫内鱼和交叉鱼依旧是需要借助于强制链的推导（或者说是通过直推的方式）才能得到删数，但这还不如使用候选数视角寻找它们。所以，宫内鱼和交叉鱼的直观用五个字形容就是“费力不讨好”。

如图所示，这是宫内三链列的直观视角。可以看到，它实际上依然借助了候选数，加入了强制链的元素。首先我们通过直观原理得到的是，r6c3(5)是直观鱼的鱼鳍。我们为了忽略它的影响，必须视作毛刺处理。

当这个候选数为真的时候，就会引出强制链，使得b7只有两处可以填入5的地方，形成区块，然后和其它位置的5形成一个普通的三链列；

当这个候选数为假的时候，我们就可以忽略它，并认为这个直观鱼成立，删数显然就是域外的所有候选数5了。

实际上可以看到，不论什么情况，红色的5显然都是可以删除的。

同样地，宫内四链列的直观思路也是完全一样的。

可以看到，我们套用之前的方式完全是一样的操作。但实际上，我们从经验上就可以看出，这种操作也只能针对于只有一个宫的宫内鱼结构才可以奏效，而且它借助的是和这个唯一的宫元素旁边无关的候选数引出的毛刺。

而实际上，两个示例都可以看到，借助毛刺并没有什么作用。因为借助的毛刺已经完成了大部分鱼结构的观察。如果你能找到两个示例的毛刺为真的情况（即左图这样），显然宫内鱼结构的构型就差不太远了。所以，宫内鱼的直观视角完全就是“费力不讨好”；当然了，在一些极端情况下，它们还是有用处的，虽然用处不太大。

1-9 交叉鱼的直观

下面我们来看交叉鱼结构的直观视角。我们按照老规矩，先看交叉三链列。

如图所示。如果r2c5(5)为假，则由于2 * 5的矩形内不含候选数5，而也满足直观鳍鱼结构的要求，所以删数应当为域外的候选数5。所以这个示例想要告诉我们的就是这一点。它依然引出了强制链的思维。我们再来看一下交叉四链列的例子。

可以从图中看出，当引出强制链的时候，最终得到了一个二链列结构，并得到了删数。而实际上你也可以看到，它已经包含了大部分原本交叉四链列结构的候选数了，这种观察视角并没有起到实质性的作用。

Part 2 飞鱼导弹和网

实际上，飞鱼导弹和网是有着密不可分的关系的，不过在飞鱼导弹里我们只字未提，原因很简单：因为讲解飞鱼导弹的时候还没学到网。那么现在我们来看看，飞鱼导弹到底和网有着什么关系。

首先我们拿出一则最标准飞鱼导弹的示例给大家看。

这个示例实际上你在前文可以找到它。这则示例的大致逻辑是，如果我们假设右图之中所有红色的删数里，任意一个是为真的，那么都会使得结构里的任意一个链接点消失，使得结构变为0网（秩为0的网），此时的所有网内的可能删数就全部成立了；但此时如果让这些删数全部成立的话，必然会使得r89里所有1、2、7全部挤入到r89c359里，结构变为1、2、7的拓展矩形的致命形式，所以出现矛盾。

从经验上来看，我们一般都会将JE原本涉及的数字作为一种链接点类型，而剩余的数字，则设为另外一种类型的链接点，并且一般而言，计算JE里涉及的数字的出现次数时，如果按照行来看，那么这些数字在转为网的时候，也都将使用行链接点视角；同样地，如果是列的话，就转为列链接点的视角。

实际上很多时候，JE都可以通过这个方式转为网的视角，而具体为什么可以这样转换，而且删数是否和JE本身可以删除的数字（含可推论带来的删数）一样呢？很抱歉的是，JE的结构过于庞大，使得结构的变化形式非常多，所以不能轻易给出删数原理和结论是否一致。比如，上图给出的是一个+1网，而稍后我们就会介绍一个转换为网视角后变为+2网的例子，它带有16个单元格，却是18个链接点。

不过，这个示例的JE视角里（左图），我并没有标注出潜在的推论删数，那么到底最终右图给出的这些删数是否和JE的所有删数是完全一样的呢？实际上并不是。网的视角的删数比JE的删数要多一些，你可以尝试推导一下。

如图所示，这个示例带有16个单元格，但拥有18个链接点。显然此时我们就不能尝试使用“预备删数”的逻辑来推导了。不过，我们可以试着改变一下思路，或许你可以发现这个技巧实际上在转换为网的时候，依然可以删数。不过，我希望你能独立思考它，虽然我也知道这一点思考和得到结果的过程很艰辛，也富有挑战性。

Part 3 SK环和网

下面我们来看一个更奇特的技巧：SK环。这个技巧可以被看作一个网。

3-1 如何转换呢？

如图所示，这便是很好的说明。可以看到，我们把行、列、宫链接点分别使用绿色、橙色和紫色标注，可以发现，恰好可以实现全覆盖，并满足0网的规则：链接点总数和单元格总数一样。所以，这个示例的删数便是所有链接点对应区域的这些数字了。

不过，我们介绍SK环结构并没有如此简单。

3-2 SK环的直观

事实上，由于结构过于特殊，我们甚至可以通过直观层面去分析SK环结构。

首先，我们观察候选数视角的SK环，可以看到候选数视角的SK环里涉及的行列链接点比较整齐，而宫链接点则显得不是特别引人注目。不过我们依然可以发现到，行列链接点涉及的数字不总是一样的，但大致的分布是两个数字一组，且以宫链接点（紫色）作为行链接点和列链接点的桥梁。而且，宫链接点在对角分布的两个宫里，数字是一样的。比如b19里的宫链接点都是2和9，而b37里则都是1和5，这是必然吗？

我们反过来，看看结构的直观模式。为了不影响你继续看候选视角，这一次我不打算把候选数全部都隐去。可以看到的是，我们以r28c28作为“轴心”，b1379四个宫的剩余提示数全部都作为结构的“支柱”。如果我们只要这些数字，那么SK环的框架就已经形成了。

此时我们仅尝试观察b1379里跟SK环有关的单元格，你就会发现，结构的链接点完全没有发生变化，不过因为结构的干扰几乎不存在了（因为是图示，所以我们把所有其它位置的确定值都拿掉了），所以可能链接点会看似变多，但依旧是满足0网的要求的。

比如这个示例里，我们把图上的链接点都标注了出来。不过，细数一下链接点总数，就可以发现，此时结构涉及一共20个链接点，因为有四个链接点是我们变为结构形式时补充上去的，此时是16\20网，所以无法直接得到SK环原本的删数。

仔细看一下，这个结构多出来的四个链接点分别在哪里：一个是c8的7、一个是r2的7、一个是c2的4，一个是r8的8，而仔细观察原本的题目里，这些数字在所在的区域下全部都有确定值，它们把这些数字的影响都排除掉了，所以SK环就直接成立了。

那么，SK环的直观具有哪些特性呢？首先结构是分属于四个宫的，并且这四个宫是类似于田字形分布的，并不是错开分布的；而且四个宫里，每一个宫都只有三个确定值，且确定值里，对角分布的两个宫里，抛开所谓的轴心不看，剩下的数字则是完全一样的。这就是SK环在直观的时候需要满足的架构。

如图所示，这便是SK环的一个基本的示例。

3-3 JE + SK = PLQ

可以从之前学习到的SK环和JE技巧来看，它们的直观层面是比较相似的。不过JE我们没有讲述直观视角（严谨地说，是只讲了JE里只有一个基准单元格的特殊JE构型，因为它比较容易直观，可以使用代数法的视角），但实际上JE可以转为网的视角，所以使得结构涉及的确定值分布也是近乎类似的。

要是我们把这两个技巧放到一起呢？

如图所示，这是同一个题目的两个不同的技巧。一个是JE（左图），一个是SK环（右图）。显然，它们的删数不都一样（当然了，JE如果使用“潜规则”，那么可能会有一样的删数效果，不过我们就不考虑了，这不是我们这里要说的重点）。

现在，我们尝试把这些得到的删数都去掉，看看还有没有结论出现。首先，我们得到它们之后，r5会出现一个1、2、3、4的四数组，这是很容易发现的，我们就不用额外作图说明了。

接着我们要看另外一处结论。

如图所示，如果我们只讨论这几个单元格，依然拥有结论。首先我们通过基础的JE逻辑，假设r5c46是a和b，那么r4c2 = a、r6c8 = b的话，显然此时位于r5的1、2、3、4四数组就剩下两个单元格了，而且只能放c和d，所以r5c2和r5c8只能一个c和一个d。这样一来的话，r45c2和r56c8就是一个跨区的四数组，不过这样看是没有什么特殊的结论的，我们无法找到合适的删数，因为我们目前不知道a、b、c、d具体指代的数字是多少。

像是图上这样，通过SK和JE结合，得到的跨区四数组，我们称之为固定产生的构型四数组（Pattern Locked Quadruple，简称PLQ）。不过，不同的SK环的提示数分布具有不同的PLQ的结论，下面我们来试试看一个示例，这个示例就拥有另外一处PLQ。

如图所示，这是同一个题目的两个不同的技巧，一个是SK环，而另外一个则是JE。需要注意的是，JE没有把其它删数标注出来，我们仅仅表达意思即可。

那么，一个引起注意的删数，就是r5上的四数组了。相信到了这里，我们都不用作出过多的说明。

现在我们要尝试解决，这四个删数到底是什么情况。我们先假设r4c2 = 7。如果r4c2 = 7，则意味着JE的基准单元格r5c46里必然会有数字7的出现，即形成7区块。不过观察b6就会发现，由于提示数的分布，这样的填法导致b6无法放入7，出现矛盾。所以r4c2 <> 7；同理，我们假设r5c2 = 7，就会使得b6仅能让r6c8 = 7，而它也是目标单元格的其一，所以依然可以得到基准单元格里含有7的结论。但这也是不可能的，因为r5c2 = 7使得r5上不允许再放入7了，所以出现矛盾。

同样地，r56c8(2)的删数也是完全一样的假设模式，所以我们可以得到图上的这四个删数结论。

在得到了上述的删数后，SK环的结构和盘面变为如图所示的这样。

现在，我们需要打开脑洞，思考r28c46这四个单元格会有如何的结论。实际上，这四个单元格是一个关于1、2、6、7的跨区四数组，即是一组PLQ。这是为什么呢？

我们仔细观察SK环里，提示数的分布情况，就会发现，1、2、6、7恰好是我们涉及的结构的数字，而且每一个宫的提示数列出来是1和2、6和7、2和6以及1和7。这样四组分布情况有一个看得出但说不出的特性。

我们为了解释这种特性，我们就将视角精细化。仔细观察SK环转换为网视角后的宫链接点，就会发现一个神奇的地方，每一个宫的宫链接点，都只有两个，而且有一个宫链接点必然占据了三个单元格，而还有一个则只占据两个单元格。且两个宫链接点必然会共用一个单元格。这些细节是我们稍后都会用到的。

思考一下。四个宫的宫链接点的分布如此“对称”，这意味着结构本身是高度对称的，这就是我们想说的特性：提示数的分布是高度对称的。

如果分布是高度对称的话，我们可以类比宇宙法的思路。由于高度对称的结构形成，必然可以得到的是，我们不能够去破坏这种对称性，否则结构会立马失去平衡，导致填数无法正确放入，出现矛盾。所以，我们为了保证结构依旧是完整和正确的，我们只能使得r28c46这四个可能会影响到结构的单元格是一个四数组。如果这四个单元格只填入两种候选数，显然是矛盾的，因为形成了UR的致命形式；如果只填入三种候选数，显然这样的填数模式影响到了高度对称的宫链接点，使得结构立刻变为不稳定状态，使得结构出现类似于宇宙法的矛盾，所以，四个单元格必须是四个完全不同的数字。

那么，这一点有什么用处呢？我们尝试枚举出所有填数情况。我们拿出r2c46进行枚举，r2c46一共存在6种不同的填数情况：

• 1和2；

• 1和6；

• 1和7；

• 2和6；

• 2和7；

• 6和7。

我们首先从1和2这一对情况说起。

如图所示，假设r2c46是1和2的数对，那么r8c46只能是6和7的数对，于是观察b39，由于刚才说到的那种分布模式，最终我们可以根据这种模式直接确定此时1、2、6的位置，那么，r56c8同时只能填入7，显然是违背数独规则的。

下面我们来看1和6的组合。

如果假设好1和6的话，我们可以发现，此时并未产生任何的矛盾。我们不能认为这种情况是错误的。所以我们先暂时放一边。

然后发现，1和7的组合依然是不行的。和上述逻辑类似，我们可以发现，r56c8都只能是7。

接下来我们发现，如果r2c46是2和6的数对的话，b17会出现矛盾，如图所示，逻辑和上面完全一样，这里就不作出说明了。

接下来是2和7的数对组合。显然这种情况依旧没有矛盾。

6和7的组合也是错误的。

这六个图我没有去掉本来删掉了的r45c2(7)和r56c8(2)，是因为使用的枚举完全没有用到这个地方的删数逻辑，所以为了示意更明确、更完整，就没有在图上去掉这些原本已经删除掉的数字。

这样我们通过枚举，就把所有情况都走了一遍，最终发现，只有1和6的组合，或是2和7的组合是满足要求的。当然，这也同时说明了一点，r5c46不能是1和6的数对，也不能是2和7的数对，否则将会和PLQ给出的其中两个单元格形成UR的致命形式。

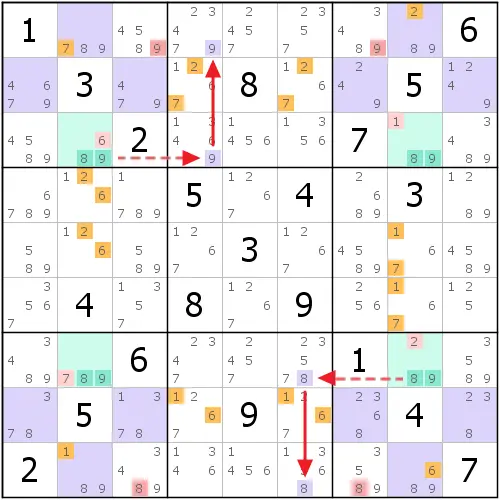
下面我们使用涂色。由于我们确定最终PLQ只有两种填数模式，我们就分两种情况进行涂色。第一种情况是左图这样，我们可以根据这种涂色模式，得到r19c28只有8和9，于是形成一个特殊的结构，看起来很像是X-Wing，而且是绑定的X-Wing。我们通过这个结构，可以直接断定，r19不能再填入其它的8和9了，因此，此时的r1c37 <> 9，r9c37 <> 8。

同理，第二种情况是右图这样。我们此时可以得到，r37c28形成类似于刚才的绑定的X-Wing结构，不过此时需要借助b28的共轭对。由于关于8和9的结构成立，使得此时r3c4 <> 9，r7c6 <> 8。由于b2存在9的共轭对，而b8存在8的共轭对，所以r1c4 = 9、r9c6 = 8。这样一来，我们依然可以得到r1和r9的其余位置不能放入9和8，所以此时r1c37 <> 9，而且r9c37 <> 8。

由此可见，我们通过费力的枚举，最终得到了应有的“回报”，这四个删数是我们预料不到的地方。

Part 4 JE的直观

又是一个优秀的标题。怎么，想让我直观JE这种破结构？当然是的。我们来看看JE是怎么转换视角的。

我们依然拿出最最标准的示例给大家。因为JE的变体类型结构实在是太多了，所以很多时候，推论的删数不一定在任意时刻都成立，所以为了阐述这里的直观视角，我选择了一个最基础的示例。这则示例在前文里已经被提及了两次，但我依旧喜欢拿出这个示例来解释一些东西，因为它最基础。

我们参照网的直观视角，将JE用直观的方式呈现出来。

如图所示，具体形成这样的形式我们就不再详细描述了，这一步其实很简单，直接画线分配填数位置就可以了。而根据上述的图上的分配形式，现在我们可以得到的是：

交叉格 + 紫色单元格 = 4套1到9

交叉格 + 橙色单元格 = 5套1到9

所以

橙色单元格 = 1套1到9 + 紫色单元格

如图所示（上述三个公式配合这个图一起理解）。注意，此时图上已经没有b9的涂色，因为b9恰好是一套1到9，我们完全可以拿来用于抵消公式里的“1套1到9”这部分。

然后，结构就成了这样。显然，此时橙色和紫色直接就是填数完全一样的构型了。不过，光是得到这个结论还不够，因为它并不足以得到删数结果。因为我们细数确定值就可以发现，橙色单元格含有8个空格，但紫色的确定值只有6个，显然会空出两个单元格，依然我们是无法确定填什么的。不过别担心，我们还有一些情况是可以立马排除的。

细看结构，由于原本JE给出的基准单元格只有1、2、7，而如果让r24c9都填入1、2、7的话，显然是不允许的，因为四个单元格都只有1、2、7是显然矛盾的。所以r24c9只能有一个单元格是1、2、7，而另外一个单元格则不允许是1、2、7。第二，基准单元格还不允许让r78c35全都是1、2、7，否则四个单元格配合r78c9构成1、2、7的拓展矩形的致命形式。所以r78c35里至少有一个数也不是1、2、7。所以，我们就可以确定1、2、7的最终填入位置了。

如图所示，我们不管r78c35里哪三个单元格是1、2、7，也不用管r24c9哪一个单元格是1、2、7，这都不重要，因为我们还有两个单元格是完全可以确定下填入1、2、7的位置的，即r2c7和r3c8，这两个单元格是一定只能是1、2、7的，否则1、2、7不够填入到橙色单元格里，使得橙色还有的其余位置必然会出现矛盾，要么四个单元格填入1、2、7三种数字出错，要么就是拓展矩形的致命形式导致的出错。

这就是JE的直观。虽说是直观，但依旧需要一点点候选数的视角来辅助我们的逻辑推理，而它恰好借用了一个完整的宫，来抵消多余的1套1到9；但比较遗憾的是，显然这种结构只能是分布呈现类似于同宫定理需要满足的样子。如果是四种数字的话，由于确定值的分布不再像这样简单，所以不便推理，很少出现这样的构型；而其它的变种就更难说了。

下面我们来尝试理解一些示例。如图所示。另外，需要你自行判断逻辑的结论，以及删数到底是如何形成的，或是能否通过直观视角删除这些标注出来的候选数。如果可以删除，请自行说明理由。不过标注的删数都是通过基础的JE的删数模式得到的删数，不代表直观视角可以删除。

至此，我们就把所有网的内容介绍完毕了。可以发现，很多技巧的直观视角都是依赖于网结构的，而在之前的内容并没有说明，把它放到最后一个技巧来进行介绍并不为过。