材料科学基础 （6.4） 三元系统相图（1）

三元系统

凝聚系统：当外界条件不变时，如果系统的各种性质不随时间而改变，则这系统就处于平衡状态，没有气相或虽有气相但其影响可忽略不计的系统。

 三元系统顾名思义，是包括三个独立组元的系统，即C=3，比二元系统更为复杂。

相律表达式：F=C-P+1=4-P

意味着在该系统中，最大自由度为4，最多有4个相共存

三元系统组成的表示：

三个主要的独立组元两两组成三条线，于是采用等边三角形来表示它们的组分组成，每一条边表示二元系统中两个组元的相对含量，所以我们也把这样的三角形称为浓度三角形。

浓度三角形的三个顶点分别代表A B C这三种物质的纯浓度点（含量为100%）

在三角形内任取一个点M，过点M做三角形三条边的平行线，就可以得到三个分别以a b c 为边长的等边三角形。由等边三角形以及相似三角形的相关知识，我们得到a+b+c=AB=AC=BC。因为一条边意味着被均分为100等分，完整的一条边意味着完整的组含量。即 a+b+c=100%

所以我们可以用 a b c 来表示各组分的含量，这也正是组分图非常重要的用途。

相图是一种工具，接下来我来介绍一下它更为详细的使用方法，即三元系统相图的性质。

三元系统相图的性质

1.等含量规则

在浓度三角形中，平行于一条直线上所有各点的组成中含对面顶点的组元量相等。

（由浓度的判断规则可以帮助理解，过该直线上的点做对面顶点边所对应的平行线，一直就是这条线本身）

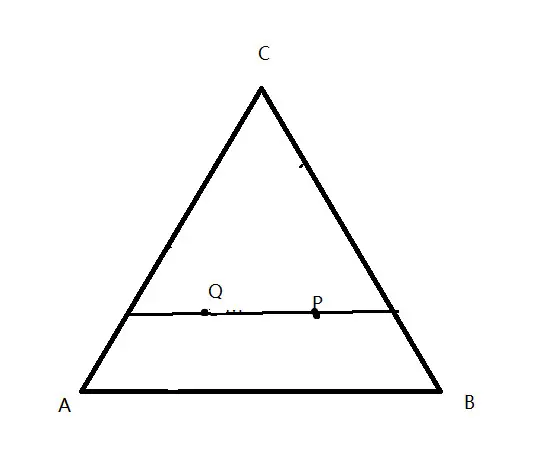
2.等比例规则

从浓度三角形的顶点向其对边作射线，线上所有点的组成中含其他两个组分的量的比例不变。

（通过做几个相似三角形可以证明）

3.背向线规则

在浓度三角性中，一个三元系统的组成点愈靠近某个顶点，该顶点所代表的组元含量就愈高，反之亦然。

4.杠杆规则

当两个组成已知的三元混合物（或相）混合成一个新混合物（或相）时，新混合物的组成点必在两个原始混合物组成点的连线上，且位于两点之间，两个原始混合物的质量之比比它们的组成点到新混合物组成点之间的距离成反比。

在分析二元系统的时候，我们讨论过杠杆规则，而在三元系统中也是类似的。

推论：由一相分解成为两相的时候，这两相组成点必分布于原始组成点的两侧，且三点成一条直线。

5.重心规则

（1）重心位置规则：M+N+Q=P，P点为低共熔点

（2）交叉位置规则：P+Q=M+N，P点为单转熔点

（3）共轭位置规则：P+Q+N=M，P点为双转熔点

下次更新将详细分析三元相图的基本过程

后记：好一点想吃圣诞芝士锅，点了之后竟然才告诉我没有了（可恶）。只好煮了香香的奶茶喝，希望身体快点好，真是根本没力气出门。