一、坐标变换

（1）坐标变换的基本思路

坐标变换的目的是将交流电动机的物理模型变换成类似直流电动机的模式，这样变换 后，分析和控制交流电动机就可以大大简化。以产生同样的旋转磁动势为准则，在三相坐标系上的定子交流电流i A 、iB 、iC ，通过三相——两相变换可以等效成两相静止坐标系上的交流电流ia 和ib ，再通过同步旋转变换，可以等效成同步旋转坐标系上的直流电流id 和iq 。如果观察者站到铁心上与坐标系一起旋转，他所看到的就好像是一台直流电动机。

异步电机的电感矩阵和转矩方程体现了电磁耦合和能量转换的复杂关系；三相原始模型复杂，简化基本方法就是坐标变换。要简化数学模型，须从电磁耦合关系入手。

能将交流电动机的物理模型等效地变换成类似直流电动机的模式，分析和控制就可以大大简化。任意对称的多相绕组，通入平衡的多相电流，都能产生旋转磁动势，当然以两相最为简单。坐标变换原则：合成磁动势相等

（2）𝑪𝒍𝒂𝒓𝒌变换：𝟑/𝟐变换

𝐴𝐵𝐶和𝛼𝛽两个坐标系中的磁动势矢量，将两个坐标系原点并在一起，使𝐴轴和𝛼轴重合（如右图所示）。三相绕组每相有效匝数为𝑁3，两相绕组等效匝数为𝑁2。三相绕组𝐴、𝐵、𝐶和两相绕组之间的变换，称作三相坐标系和两相正交坐标系间的变换，简称3/2变换。按照磁动势相等的等效原则；变换前后总功率不变。

因此有：

考虑到变换前后总功率不变，则有：

三相坐标系变换到两相 正交坐标系（简称 3/2变换）的变换矩阵：

两相正交坐标系变换到三相坐标系（简称 2/3变换）的变换矩阵：

又考虑到 𝑖𝐴+𝑖𝐵+𝑖𝐶=0 ，可以写作:

电压变换阵和磁链变换阵与电流变换阵相同。

(3)𝑷𝒂𝒓𝒌变换： 𝟐𝒔/𝟐𝒓变换

两相静止绕组，通以两相平衡交流电流，产生旋转磁动势。如果令两相绕组转起来，且旋转角速度等于合成磁动势的旋转角速度，则两相绕组通以直流电流就产生空间旋转磁动势 。即 从静止两相正交坐标系 𝛼𝛽到旋转正交坐标系 𝑑𝑞的变换，称作静止两相 -旋转正交变换，简称 2𝑠/2𝑟变换 。

电流之间存在下列关系：

因此有 旋转正交变换矩阵式：

即有静止两相正交坐标系到旋转正交坐标系的变换阵：

旋转正交坐标系到静止两相正交坐标系的变换阵：

同理可知：电压和磁链的旋转变换阵与电流旋转变换阵相同 

▲异步电动机定子绕组是静止的，只要进行 3/2变换( 𝐶𝑙𝑎𝑟𝑘变换)就行了。 

▲异步电机转子绕组是旋转的，必须通过 3/2变换和旋转到静止的变换（𝑃𝑎𝑟𝑘变换），才能变换到静止两相正交坐标系。

二、Simulink仿真的实现

1、电流跟踪PWM技术

由上文所诉电流跟踪原理，可以搭建如下电流跟踪PWM的Simulink模型：

滞环比较器的设定：

2、SVPWM 技术

搭建Simulink的SVPWM控制模型大致分为：𝛼𝛽变换 、𝑈𝑟𝑒𝑓判断扇区及计算PWM占空比、输出PWM信号几个流程。

（1）𝜶𝜷变换

三相绕组𝐴、𝐵、𝐶和两相绕组之间的变换，称作三相坐标系和两相正交坐标系间的变换，简称3/2变换。按照磁动势相等的等效原则；变换前后总功率不变。

三相坐标系变换到两相 正交坐标系（简称 3/2变换）的变换矩阵：

由此矩阵搭建𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘模型

（2）𝑼𝒓𝒆𝒇与扇区判断

其中𝑈𝑟𝑒𝑓是期望电压矢量的模，角度𝜃是它与𝛼轴的夹角，，其中m是调制系数，是逆变器主电路的直流母线电压。当m>1时会出现过调制，波形失真，此时𝑈𝑟𝑒𝑓超出了正六边形的内切圆范围。而𝑈𝑟𝑒𝑓的最大值就是非零电压矢量的值，为 。

𝛼轴即实轴𝑅𝑒与𝑈1参考位置重合（如图八）；β即虚轴。在扇区Ⅰ中：

当：

即：

表述为：

其他扇区按照同样的方法，以此类推，得到：

由此可以定义以下参考变量：

再定义：，则A=1，否则A=0；，则B=1，否则B=0 ，则C=1，否则C=0。

ABC由判断扇区公式可知道组合为6种。𝐴、𝐵、𝐶取不同的组合对应着不同的扇区，此可由𝐴、𝐵、𝐶的组合判断所在的扇区。为区别扇区的六种状态，令：𝑁 = 𝐴 + 2𝐵 + 4𝐶，则𝑁具体对应关系如表1所示：

表1 扇区值与扇区号对应表

由上可以搭建如下扇区判断的𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘模型：

（3）计算SVPWM占空比

SVPWM的理论基础是平均值等效原理，即在一个开关周期内通过对基本电压矢量加以组合，使其平均值与给定电压矢量相等。 在某时刻，电压空间矢量旋转到某一个区域中，可以由这个区域的两个相邻非零矢量和零矢量在时间上的不同组合来得到。先作用的称为主矢量，后作用的称为辅矢量。作用时间分别为，零矢量作用时间为。 如图八所示，根据平均值等效原则可以得到下列等式：

其中分别为的作用时间。为合成矢量与主矢量的夹角，要合成所需电压，需要计算。

由正弦定理得：

得：

于坐标系中可得：

又不能超过，所以取同理可以推导其他扇区各矢量作用时间，为了方便判定，可以令

搭建计算XYZ的𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘模型为:

表2 各个扇区的作用时间

如果当，必须进行调制（等比例缩小原则）处理，则令：

𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘实现如下：

（4）SVPWM 的实现

由期望输出电压矢量的幅值及位置可确定相邻的两个基本电压矢量以及它们作用时间的长短。以开关损耗和谐波分量较小为原则，在减少开关次数的同时，尽量使SVPWM输出波型对称，以减少谐波分量。 采用零矢量分散的实现方法，以第Ⅰ扇区为例子：按开关损耗较小的原则，选取零矢量。将零矢量平均分为4份，在开关周期的首、尾各放1份，在中间放两份，将两个基本电压矢量的作用时间平分为2份，插在零矢量间。

确定扇区矢量切换点，令：

𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘实现如下：

其中：Ta即从开始到零矢量U0第一次作用完时间 t0/4，Tb为从开始（经过零矢量第一次作用后）到u1第一次作用完所用的时间，Tc为从开始（经上述过程）到u2第一次作用完成所用的时间。接着如果要继续进行作用应该是零矢量u7作用t0/2 ，接着继续是u2（作用t2/2 ），然后u1（作用 t1/2），最后零矢量u0作用t0/4。

推广到各个扇区，如表3所示：

表3 各个扇区电压切换表

三相电压开关时间切换点与各扇区的关系如表4所示：

表4 三相电压开关时间切换点

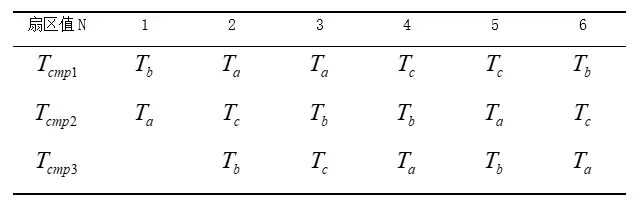
搭建有以下𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘模型：

（5）SVPWM信号的产生

将三相电压开关时间切换点与调制波进行比较，输出SVPWM信号。𝑆𝑖𝑚𝑢𝑙𝑖𝑛𝑘模型如下：

（6）总SVPWM信号模型

百度网盘链接

链接：https://pan.baidu.com/s/1Un5eiuTTtktDSTaed1bjbg?pwd=6xch 

提取码：6xch