量子场论(九):洛伦兹代数和庞加莱代数
来研究(8.19)式。考虑无穷小庞加莱变换,左边化为:
(8.19)右边第一项变成:
(8.19)右边第二、三项变成:
对比发现生成元算符间的对易关系:
以生成元的6个分量作为基底张成线性空间,以对易关系(9.4)定义乘法,则两个矢量的乘积还是这个空间中的矢量,即乘法运算封闭,则称此线性空间为洛伦兹代数。
维李群的群空间由
个连续实参数
描述,可以看做
维微分流形,O(N)和SO(N)是
维李群,U(N)是
维李群,SU(N)是
维李群,对于
维李群的一个
维线性表示,在恒元附近,无穷小变换对应的表示矩阵可以展开为:
其中是
个独立的
阶生成元矩阵,生成元满足对易关系:
其中实数称为结构常数,满足
不同的表示具有不同的生成元,不过,同一个李群的所有线性表示的结构常数都是一样的,描述了李群的局域性质。阿贝尔群的结构常数是零。生成元的对易子又叫李括号,是一种乘法运算。在生成元为基底张成的线性空间中,李括号运算是封闭的,构成代数,称为李代数。李代数刻画李群在恒元附近的局域结构。
洛伦兹群是一个六维李群,它的李代数就是洛伦兹代数。洛伦兹群任何线性表示的生成元都要满足洛伦兹代数关系(9.4)式。反过来,通过构造满足洛伦兹代数关系的生成元,,可以得到洛伦兹群的线性表示。
把生成元的6个分量组合成两个三维矢量算符。空间部分组合为:
时空混合部分组合为:
那么与
的对易关系为:
而我们容易知道:
因此对易关系为:
又引入两个三维矢量:
是做洛伦兹变换时绕
轴转过的角度,
是沿
轴的快度。从而,无穷小洛伦兹变换化为:
对于绕轴的空间旋转变换
因此有:
由初始条件得到相应的量子旋转变换:
空间旋转对称性对应着角动量守恒定律,因此,就是角动量算符在
轴上的分量。同理,
就是总角动量算符。空间旋转群SO(3)是洛伦兹群空间部分的子群,总角动量算符
是量子空间旋转变换的生成元。而(9.12)式就是SO(3)的李代数关系,结构常数就是
。
SO(3)和三维李群SU(2)联系密切,在SU(2)的基础表示中,三个生成元矩阵为:
其中是3个2×2的泡利矩阵:
它们很神奇,既厄米又幺正:
泡利矩阵们的乘积们:
总结起来:
可以得到泡利矩阵的对易子和反对易子:
因此,SU(2)生成元的对易关系为:
因此发现,SO(3)和SU(2)的李代数关系完全一致,说明两个李群在恒元附近的局域性质相同。
但是,SU(2)群的整体拓扑性质与 SO(3)群不一样。SU(2) 和SO(3)的群空间都是连通的,更仔细地讲,SU(2) 的群空间是单连通的,连接群空间中两点的任意两条曲线可以连续地形变成彼此,等价地,群空间内任意一条闭合曲线可以连续地收缩为一点。SO(3)的群空间是双连通的,即连通度为 2,连接群空间中两点的曲线分成两类,同一类曲线能够连续地变化成彼此,不同类曲线则不能;相应地,闭合曲线也分为两类,有一类能连续收缩成一点,另一类不能。
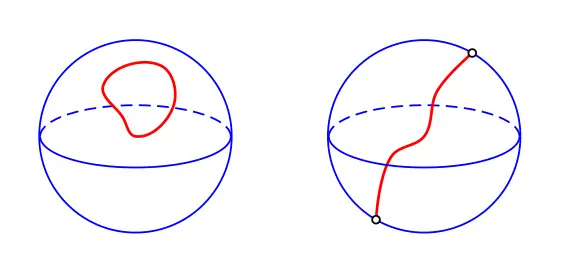
续收缩成一点。右图中的闭合曲线在对径点处发生跳跃,不能连续收缩成一点。
另一方面,是增速算符。
与
的对易关系为:
自身的对易关系为:
归纳起来,有:
这是洛伦兹代数关系的另一种表述。可见,三个生成元自己就可以构成封闭的代数,而三个生成元
则不能。
来研究(8.20)式。考虑无穷小庞加莱变换,左边化为:
(8.20)式右边给出:
得到对易关系如下:
以生成元和
的10个独立分量作为基底张成的线性空间,用(9.4)(9.31)(9.32)定义乘法,就构成了庞加莱代数,这是十维庞加莱群的李代数。洛伦兹代数是庞加莱代数的子代数。
令则
进一步推出:
整理一下,有:
(9.28)(9.37)(9.38)是庞加莱代数关系的另一种表述。
当时,由(8.11)式得到:
若不依赖于
则由初始条件得知量子时间平移变换为:
它将态矢从时刻平移到
时刻。时间平移对称性对应着能量守恒定律,因此
就是哈密顿算符。
当时,由(8.11)式得到:
则由初始条件得知量子空间平移变换为:
它将态矢从位置平移到
位置。空间平移对称性对应着动量守恒定律,因此
就是动量算符。因此,
是四维动量算符。在量子力学中,与哈密顿算符对易的量是守恒量,从而(9.38)式意味着总动量与总角动量守恒。
一般的量子时空平移变换可以表达为:
满足:

