格林公式和高斯公式表示什么意思

按照对坐标的曲线积分的意义，它表示的是一个变力沿着下图平面中的闭合曲线所作的功。

再看格林公式，右边是变力沿闭合曲线所做的功，而左边是一个二重积分。根据图1，我们可以认为，变力所做的功被平均分配到了闭合曲线所围成的曲面上。因此图2左边的函数

应该可以看作是图1中功在曲面上的面密度。

图2中功的面密度是变化的，也就是说，每个点的密度都不一样，这是因为x,y可以是任何一个点的坐标。

作者在《从定义理解散度的含义》一文中，提到如下理解方法：

我们知道，任意两个不同的数字之间必然存在着差值，而任何一个确定的数字都对应着数轴上的一个点，现在我们假设图3是数轴上间隔任意小的三个点，但不管它们之间的间隔多小，只要它们不相同，就必然存在间隔。这个时候我们就可以假设，用一个长度为Δx的篮子装下数轴上的一个点，这个篮子的长度比数轴上任意两个点之间的间隔都要小，也就是我们所说的无穷小，也就是它的长度无法用任何一个确定的数字表示，但它又比0大，所以它能装下一个大小为0的数字，而且只能装下一个点，如果能装下两个点，而两个点对应两个确定的数字，它们之间也就必然存在可以用确定的数字表示的间隔，那就不是无穷小。

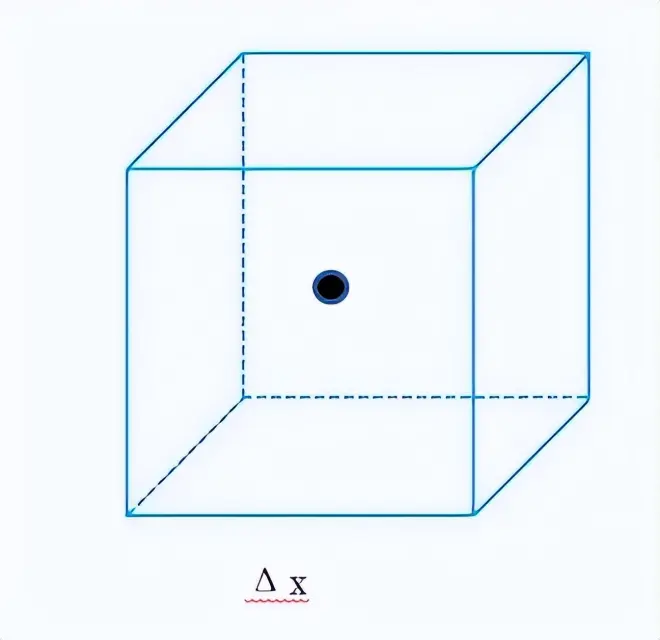
按照上述假设，我们可以假设上图长度为Δx的立方体只能装下空间中的一个点，这就是图4定义中Δv的含义。

同样，我们可以假设如下的矩形只包含平面中的一个点：

于是，图2中左边的积分就好理解了，那就是平面中每一个点的功的密度求和。

按照同样的方法，我们就可以理解高斯公式的意义了。因为高斯公式的右边表示的是一个速度为v的流体流过曲面的流量：

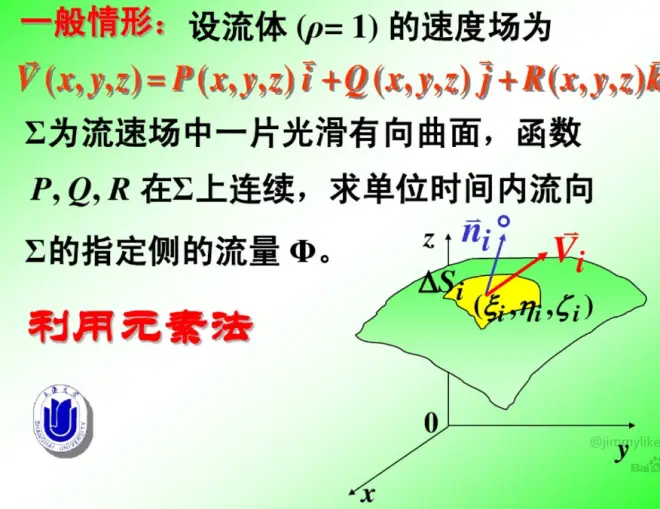
那么，图6高斯公式的左边，就应该是由图7的曲面所围成的封闭空间立体中每一个点的流量之和：

上图中的封闭曲面可以看作是由一个个图4中只包含一个点的立方体构成。

而图6左边的函数

就是空间每一个点的流量。散度正是这样定义的：

综合一下：

1：一维、二维、三维甚至n维空间，我们都可以由无穷小的定义，构造出一个只包含一个点的元素，从而为n维空间的积分提供依据。

2：格林公式和高斯公式分别是二维和三维空间上的密度积分。