关于我与高中总样本方差的抗争经历

不知大家有没有见过这种奇怪的题

在不知道个体样本的数据情况下求一些奇奇怪怪的东西 而我便是第一次见到这种题时有些头疼 z肯定是比较好求的，这个是非常好拿分的

只需要用基础的平均数算法就可以轻松的算出来z的数值 但是接下来到了方差......出于我对方差的熟练度并不是很高，而且使用率对我来讲也不算大，我便草率的认为方差是这样算的（与z的公式一致，就是换了个数）

很明显，都这么说了，我最后的结果肯定是一个大红叉，如果题碰巧的话还是有可能算对的，不过这种情况不多 于是我便去询问了老师总样本方差怎么求，老师给出的答案是这样的

但是在我第一次抄的时候是这样的（与上图相比少了两个平方）

见到这么长的式子那我自然是不愿意去记，于是我决定把z值代换一下求出最后最简便的结果，于是当天我在宿舍研究了一中午，写出来大概是这个样子的（没有平方导致的）

就是说我推导了半天结果最后又导回来了，给我同学都看乐了，不过我最终还是打算问问我到底哪里写错了，最后才发现是一开始就把公式写错了，搞得挺难绷的，我一直都以为是我哪里算错了，找了有十几分钟吧 我便一直在想这东西这么长怎么可能会有简便的式子呢，这不会就是最简便的吧 于是我又开始了推导...

过程如下

首先肯定还是把大括号里面的东西单独拿出来，外面太麻烦了，然后简单的做一下乘法

接下来把z值带入，准备通分合并

合并之后是这个样子的

提出来一个n1，再提出来一个n2，由于是两个数相乘然后平方，所以不会用到平方和公式，写出来就是这样

a-b的平方与b-a的平方是一样的，就如1-3的平方与3-1的平方均为4一样，所以这两项是可以合并的

无需通分，继续合并，并提出n1+n2

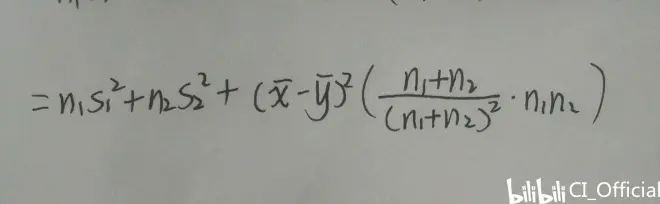
消掉n1+n2，整理可得

然后再把外侧的n1+n2拽下来，一个长长的式子就变成了这样

怎么样？是不是很简单啊？ 至少这一战之后，我的内心是妈妈生的了，话说这一次我的公式不会又从头写错了吧，2333...写错了再来一遍就可以了，持之以恒还是有一些必要的吧 如果有一些更好的解法或算法，可以在评论区留言