高中数学基础与解法全集(涵盖所有)|长期更新|从零开始拯救所有学渣!通俗易懂|高

(仅做参考)
- 内容大概有:
1.函数的基本概念.
2.值域(上).
3.单调性与最值基本概念.
4.函数的奇偶性.
5.对勾函数的性质.
6.函数奇偶性完全突破.
7.幂函数的基本概念.
8.指数函数的基本概念.
9.对数的定义.
10.对数的运算法则.
11.对数函数的图像与性质.
12.初等函数(从一到无穷大系列).
13.指数与对数的运算解析.
14.指数/对数大小比较考点解析.
15.初等函数的图象与性质.
16.等式与不等式的性质.
17.基本不等式.
18.‘1’的代换.
19.基本不等式中的‘凑形’.
20.基本不等式(从一到无穷大系列).
21.任意角的度数.
22.弧度制与扇形面积公式.
23.任意角的三角函数.
24.同角三角函数的基本关系.
25.三角函数的诱导公式.
26.三角函数的图象与性质.
函数的基本概念
求复合函数的定义域:已知y=f(x)的定义域是 A,求y=f[g(x)]的定义域,只需要根据 g(x)∈A,求出x的范围,就是所求定义域
- 把括号里的当作一个整体带入
- 前面都是f,所以对应法则一样,在抽象函数中:对应法则相同的情况下,括号内的取值范围相同!!!

值域(上)
- 万一遇到单调性不一样的函数,有可能这一段里的最值取在中间而不是两边!这时候直接代入就无法算出最值

1、将x用其他字母替代后,写出x与字母的关系式,并根据x的范围求出字母的范围
2、然后根据上面求到的字母范围来代入最大最小值,求出y也就是值域范围
总结:一次分式的求值域问题运用到参数分离和换元法

- 因为每个值域中的Y都有一个X与之对应,则X存在,想要有X也就是解则需要德尔塔≥0,否则无解,而德尔塔式子又关于Y,则德尔塔≥0可以求出Y的范围也就是值域

图中t之所以可以大到正无穷,是因为(t-1/2)'2是个完全平方式,完全平方式≥0,而前面有负号,所以为负无穷
单调性与最值基本概念

- 单调递增:X1<X2←→F(X1)<F(x2)
- 单调递减:X1<X2←→F(X1)>F(x2)
- 例题:

解答过程:
- 取值(任取)
- 作差
- 变形
- 定号
- 下结论
函数的奇偶性
- 奇函数关于原点中心对称,偶函数关于y轴对称.
- 奇函数原式f(-x)=-f(x) 两边同时乘负一就可以变成f(x)=-f(-x)


- 如果关于原点对称的话y轴可能会有两个点,就不是函数了因此这里的x不等于零(无解)
- 对勾函数:F(x)=x+1/x(奇函数)
先单调递增后单调递减再单调递减后单调递增

- 狄利克雷函数:是一个定义在实数范围上、值域不连续的函数。狄利克雷函数的图像以Y轴为对称轴,是一个偶函数,它处处不连续,处处极限不存在,不可黎曼积分,( 黎曼积分也就是所说的正常积分定积分)这是一个处处不连续的可测函数。【来自百度百科】
- 狄利克雷函数既不单调递增也不单调递减

对勾函数的性质‹建议学完基本不等式后再看›
对勾函数:y=x+k/x(k>0)
定义域:0到正无穷和负无穷到0,不包含原点(-∞,0)∪(0,+∞)


- 由对勾函数的性质可知g(x)=x+1/x的两个端点坐标为(-1,-2)(1,2)经过平移后得到f(x)的坐标为(0,0),(2,4)
- 对称中心为(1,2)

根据换元法t得到的y的最小值就是答案
换的只是元,所以需要把t加上2求得x,而不用上加下减什么的(橘字提醒 感谢!!!)
均值不等式公式:所以f(x)min=2/根号ab【最值定理:以知x,y都是正数(1)若x+y=s‹s为正值›,则当且仅当x=y时,xy取得最大值s²/4.(2)若xy=p‹p为定值›,则当且仅当x=y时,x+y取得最小值2根号p.】


函数奇偶性完全突破(中档)

- 奇函数原式f(-x)=-f(x) 两边同时乘负一就可以变成f(x)=-f(-x) 偶函数f(x)=f(-x)
- 奇函数F(0)=0不一定成立 必须定义域包含零点
幂函数的基本概念

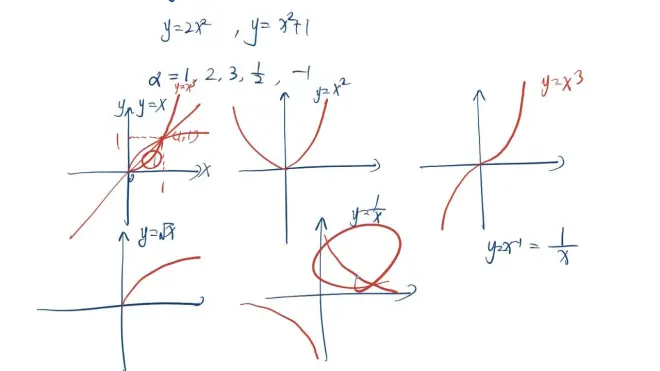
- y=x^a (系数为1,且只有一个自变量a)
例如:y=2x²,y=x²+1这些式子都不是幂函数
- 常见形式:a=1,2,3,1/2,-1.
- 重点:所有的幂函数都过(1,1)这个点.‹1的所有次方都得1›




指数函数的基本概念

- y=a^x (a为常数且以a>0,a≠1)(系数为1,且只有一个自变量x)
例如:y=2^x+1,y=2×3^x,y=3^x+1这些式子都不是指数函数
- 所有的指数函数都过(0,1)这个点





对数的定义

- a^x=N(a>0且a≠1)←←→→x=㏒aN(a为底数N为真数)›读作以a为底N的得数.‹
例:2^x=8,x=3←←→→3=㏒28
- 常用对数:

1.以十为底:㏒10N=lgN.
例:㏒10 100=lg100,则10^x=100,x=2.
2.自然对数:㏒eN=㏑N.
例:㏒e e^3=㏑e e^3,则e^x=e^3,x=3.




对数的运算法则


1.对数的加法:㏒aM+㏒aN=㏒aMN.
2.对数的减法:㏒aM-㏒aN=㏒a(M/N).
3.对数的甩x法‹doge›:㏒aB^x=x㏒aB
- 第三个我的理解是:指数中有式子(a^B)^x=a^Bx;将它们化为对数则为㏒aB^x=㏒aB+㏒ax=x㏒aB.(将㏒a看作一个整体.)


- 对数的换底公式:

- 一般的,若a>0,b>0,c>0,则a≠1,c≠1,则㏒aB=㏒cB/㏒ca.
- 令c=B,则㏒cB/㏒ca=㏒BB/㏒Ba=1/㏒Ba=㏒aB.(底数和真数互换,两者是倒数的关系)
对数函数的图像与性质
y=㏒ax(a>0且a≠1)
定义域:(0,+∞) 值域:R
过定点(1,0),即x=1时,y=0.

1.当a>1时:{当x>1时,y>0 ; 当0<x<1时,y<0.
2.当0<a<1时:{当x>1时,y<0 ; 当0<x<1时,y>0.
【当x不变时,a>1,a↑y↓ .0<a<1时,a↓y↑.当1>a>0时,a越小,图像越接近x轴.】


记住a^loga (b)=b

初等函数(从一到无穷大系列)






指数与对数的运算解析
指数a^x=B(a>0且a≠1)←→对数x=㏒aB.






1.换底
2.换元
3.计算,注意是否合题意
4注意验算
(复制来的么么哒)
指数/对数大小比较考点解析





初等函数的图象与性质(中档)







等式与不等式的性质







基本不等式

- 基本不等式:当x,y>0时,则x+y/2(算数平均数)≥√xy(几何平均数),当且仅当x=y时不等式取等号.



‘1’的代换



基本不等式中的‘凑形’(中档)

- 2x+y的最小值为9.



基本不等式(从一到无穷大系列)


任意角的度数
- 顺时针旋转为正角.
- 逆时针旋转为负角.
- 零角:始边与终边相同的角为零角.
在坐标轴中任意角的始边一般在x轴正半轴上

[将终边相同的角设为贝塔b 任意角度为阿尔发a k为整数可为正可为负]

!!!注意:第几象限角是不包括边界的!!!直角在y轴上不属于任何象限.

- 锐角、直角、钝角都是在0°—180°中进行的定义 范围以外的角不能那么定义 所以锐角、直角、钝角都是正角.
(拓展<不重要>:锐角大于0°小于90°.大于直角而小于平角的角叫做钝角,钝角大于90°而小于180°.小于平角的角叫做劣角,锐角、直角、钝角都是劣角.大于平角小于周角的角叫做优角,优角大于180°而小于360°.)

弧度制与扇形面积公式

弧度制指用弧长与半径之比度量对应圆心角角度的方式
- 360°---2π.
- 180°---π.
- 1°---180分之π.

[1度=60分]

扇形的面积公式:S扇=(n/360)πR²,S扇=1/2lr(知道弧长时),S扇=(1/2)θR²(θ为以弧度表示的圆心角),S扇=(lR)/2(l为扇形弧长).R是扇形半径,n是弧所对圆心角度数,π是圆周.

- 每个π对应着180°[弧度转角度]
- 每1°对应着180°分之π[角度转弧度]

- L≤2πr.
任意角的三角函数

- 将x看作邻边y看作对边.
- 口诀:全是天才 [第一象限都说正的,第二象限sin是正的,第三象限tan是正的,第四象限cos是正的]

- 2kπ:2π表示360度,k表示转了多少圈
- 终边相同的角它们的三角函数都相同

- y=sin x 正弦函数.
- y=cos x 余弦函数.
- y=tan x 正切函数.

同角三角函数的基本关系

- 如图已知终边在平面圆的坐标(x,y)作三角形
单位圆的半径为1.
所以sin a=y.【sin a=√x²+y²/y】 cos a=x.【cos a=√x²+y²/x】 tan a=x分之y.
根据三角形的勾股定理得出:
1.cos a²+sin a²=1.
2.tan a=cos a分之sin a.[cos a≠0,即a≠2/π+kπ,k∈z.]

注意:坐标轴不包括在任何象限内.


三角函数的诱导公式
正弦:y=sin a. 余弦:y=cos a. 正切:y=tan a.

结论:sin a为奇函数,cos a为偶函数,tan a也为奇函数.

在三角函数的诱导公式中,在第一象限满足的性质,在其他三个象限也基本满足.
【余切函数cot与正切函数互为倒数】

- 奇变偶不变,符号看象限.
k为奇数时sin变cos[或cos变sin],k为偶数是sin,cos都不变.
假装a角在第一象限,再画图看象限得出符号.
- 哪怕题目给了α是钝角,也假装α在第一象限再用口诀.
- 口诀:全是天才 [第一象限都说正的,第二象限sin是正的,第三象限tan是正的,第四象限cos是正的]



三角函数的图象与性质

周期:如果存在一个非零实数T,使得F(x)=F(x+T).我们就称T为F(x)的一个周期. 若f(x)定义域为a,则需满足f(x)∈a,f(x+T)也∈a.
(平移:x左加右减,y上加下减.)
正弦函数与余弦函数之间的关系:y=sin(x+π/2)=cos x.


