控制系统仿真(MATLAB版)(七)
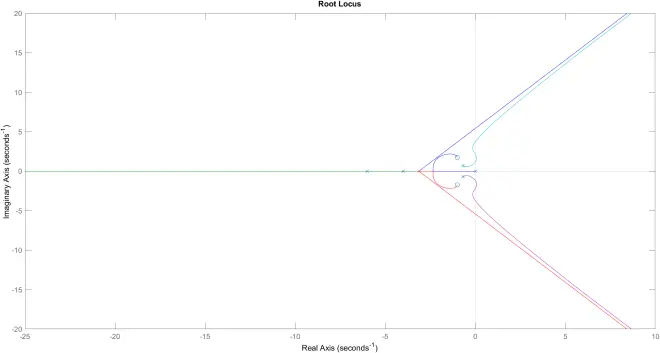
根轨迹渐近线的绘制

>> G = tf([1 2 4],conv([1 4 0],conv([1 6],[1 1.4 1])));
>> rlocus(G)
>> hold on
>> thga = -9.4/3;
>> Gc = zpk([],[thga thga thga],1);
>> rlocus(Gc)
>>
判断系统的稳定性
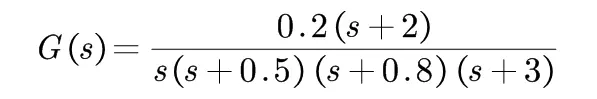

一、闭环特征根的大小
1+GH = 0(不够准确,指闭环特征根)
>> G = zpk([-2],[0 -0.5 -0.8 -3],0.2);
>> sys = feedback(tf(G),1); %注意是闭环
>> roots(sys.den{1})
ans =
-3.0121 + 0.0000i
-1.0000 + 0.0000i
-0.1440 + 0.3348i
-0.1440 - 0.3348i
或者
>> eig(sys)
ans =
-3.0121 + 0.0000i
-1.0000 + 0.0000i
-0.1440 + 0.3348i
-0.1440 - 0.3348i
所有闭环极点位于s平面(虚轴)左侧,系统稳定
>> pzmap(sys)
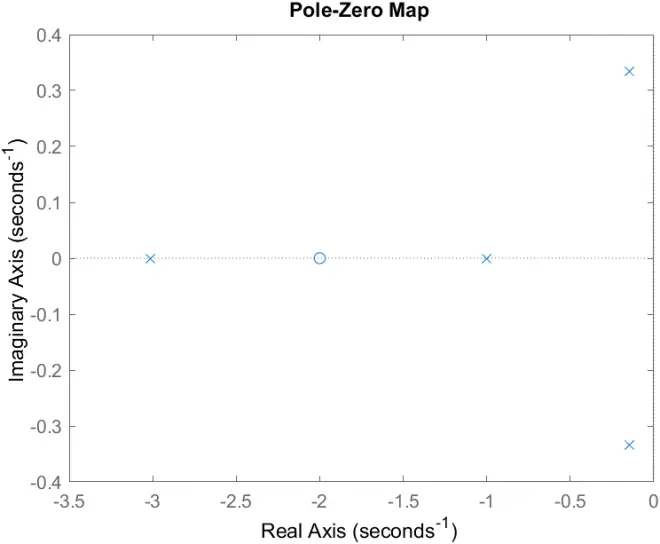
在MATLAB中,有更直接的判断方法
>> isstable(sys)
ans =
logical
1
>> allmargin(G) %这里用的是开环传递函数
ans =
struct with fields:
GainMargin: 4.7503
GMFrequency: 0.7071
PhaseMargin: 44.5277
PMFrequency: 0.2770
DelayMargin: 2.8058
DMFrequency: 0.2770
Stable: 1
4.2
求动态误差系数
>> syms s
>> G = 50*(s+2)/(s^3+2*s^2+51*s+100);
>> kp = limit(G,s,0)
kp =
1
>> kv = limit(s*G,s,0)
kv =
0
>> ka = limit(s^2*G,s,0)
ka =
0
4.4
>> G = tf([-0.5 1],conv([0.5 1],conv([0.2 1],[0.1 1])));
>> rlocus(G)
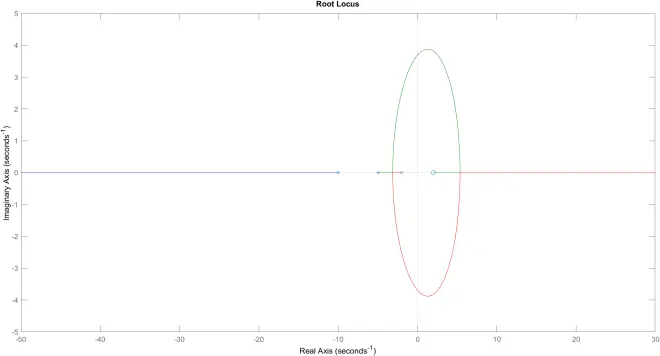
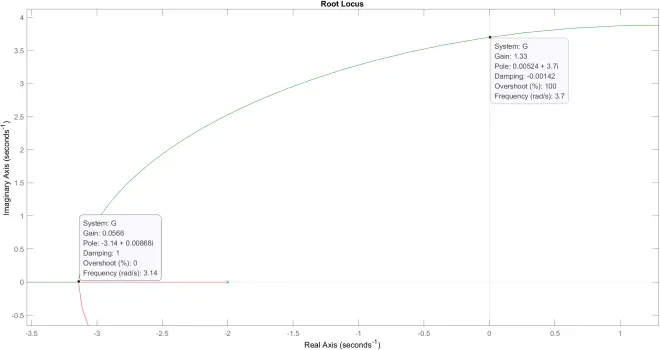
闭环系统稳定的K
0 < K <1.33
>> G = 1.33*tf([-0.5 1],conv([0.5 1],conv([0.2 1],[0.1 1])));isstable(feedback(G,1))
ans =
logical
0
>> G = 1.32*tf([-0.5 1],conv([0.5 1],conv([0.2 1],[0.1 1])));isstable(feedback(G,1))
ans =
logical
1
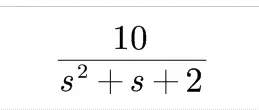
4.5求动态误差系数
>> syms s
>> G = 10/(s^2+s+2)
G =
10/(s^2 + s + 2)
>> kp = limit(G,s,0)
kp =
5
>> kv = limit(s*G,s,0)
kv =
0
>> ka = limit(s^2*G,s,0)
ka =
0
4.6
>> G1 = tf(5,conv([1 1 0],[0.1 1]));
>> sys1 = feedback(G1,1);
>> G2 = tf(20,conv([1 1 0],[0.1 1]));
>> sys2 = feedback(G2,1);
>> pzmap(sys1)
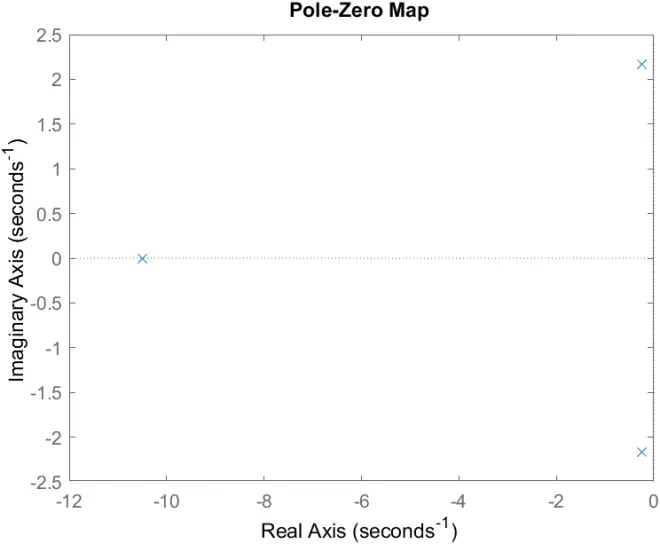
pzmap(sys2)
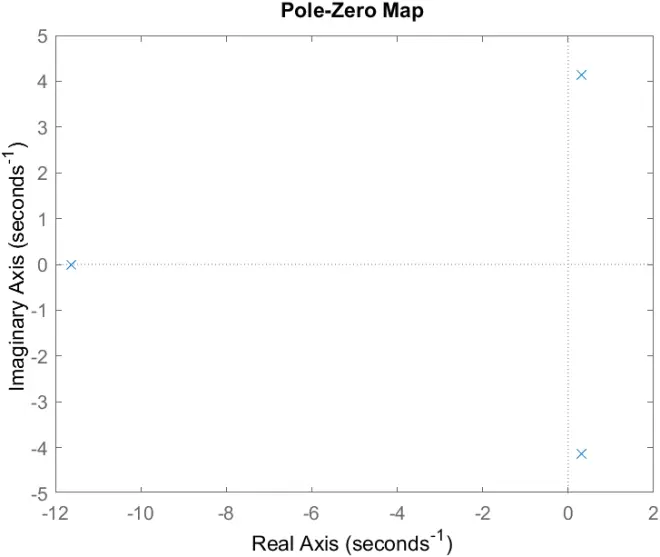
>> [mag,phase,w] = bode(G1);
>> margin(mag,phase,w)
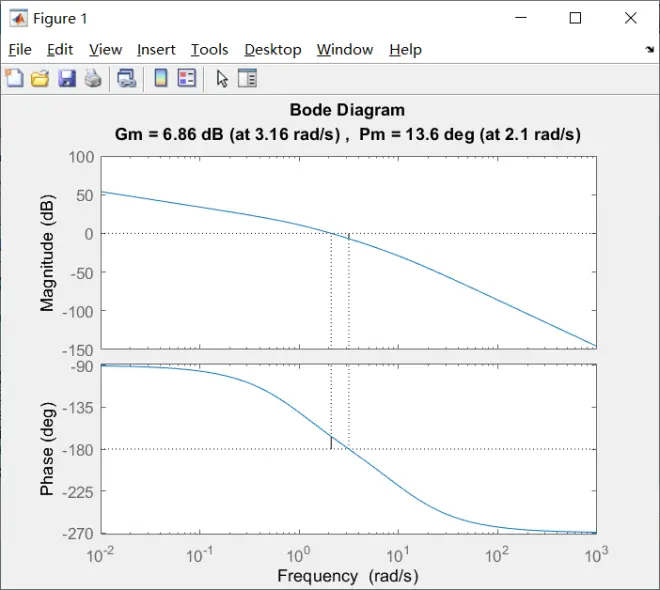
>> [mag,phase,w] = bode(G2);
>> margin(mag,phase,w)
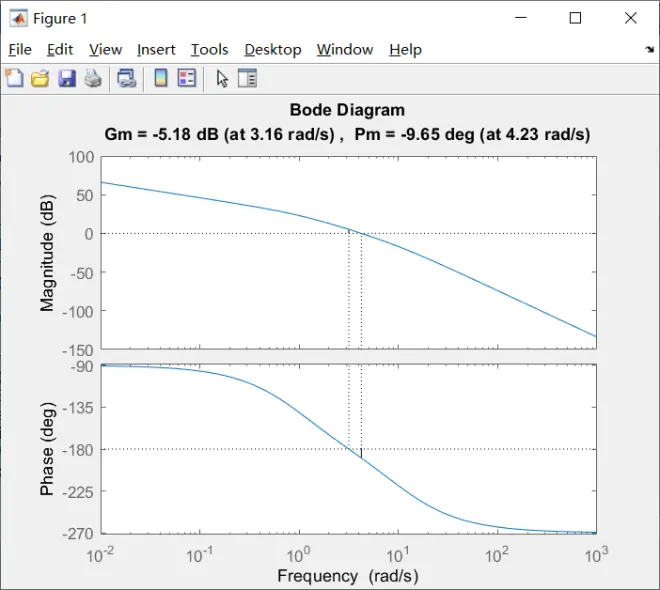
4.7
>> s = tf('s')
s =
s
Continuous-time transfer function.
>> G = 16*(19*s+1)*(0.44*s+1)/((0.625*s+1)*(0.676*s-1)*(43.5*s-1)*(0.033*s+1)*(0.0004*s^2+0.015*s+1))
G =
133.8 s^2 + 311 s + 16
------------------------------------------------------------------------------
0.0002426 s^6 + 0.01647 s^5 + 0.8832 s^4 + 18.43 s^3 - 0.2936 s^2 - 43.5 s + 1
Continuous-time transfer function.
>> [Gm,Pm,Wcg,Wcp] = margin(G)
Gm =
4.8847
Pm =
53.1362
Wcg =
32.1207
Wcp =
7.2063
>> margin(G)
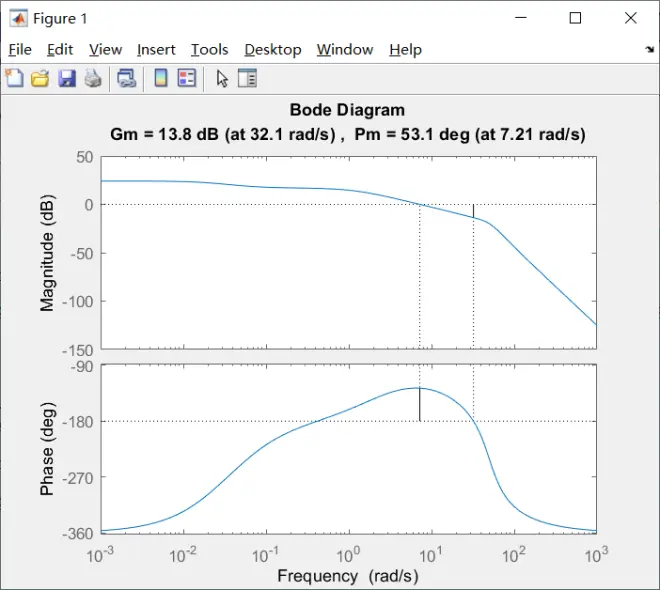
4.8
>> G = tf([1 1],conv([1 0 0],[0.1 1]));
>> [Gm,Pm,Wcg,Wcp] = margin(G)
Gm =
0
Pm =
44.4594
Wcg =
0
Wcp =
1.2647
%% 该系统稳定
>> margin(G)
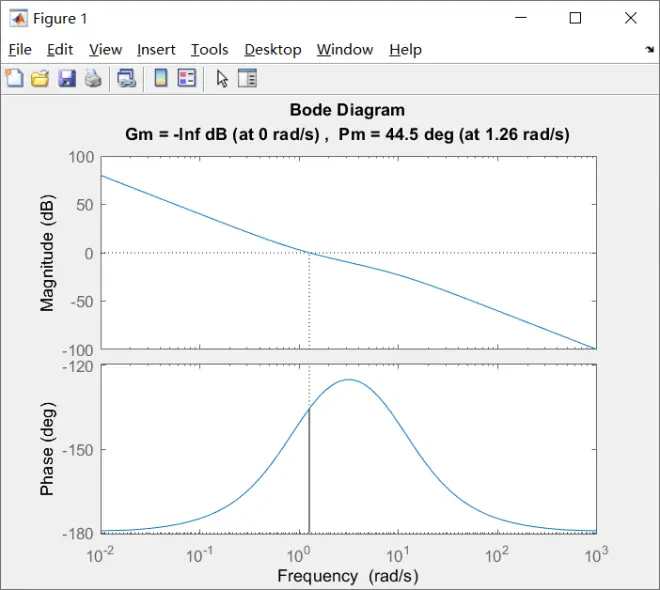
>> figure
>> bode(G)
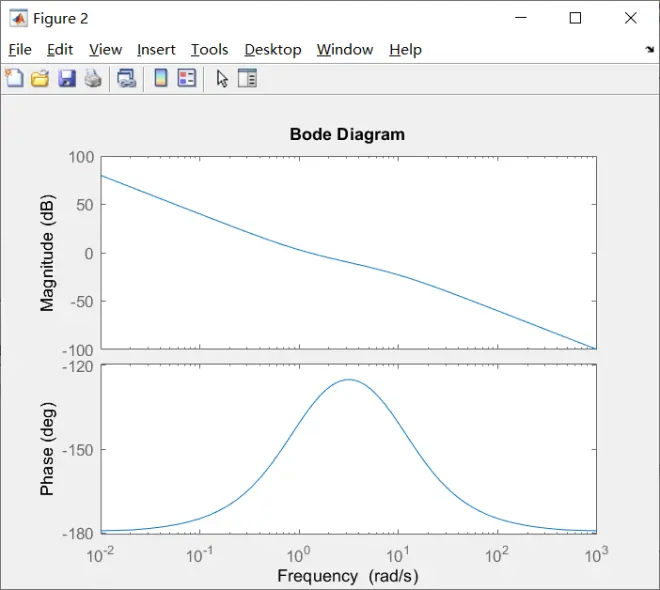
4.10

>> G1 = zpk([],[-1;-2;-5],2*5*10)
G1 =
100
-----------------
(s+1) (s+2) (s+5)
Continuous-time zero/pole/gain model.
>> nyquist(G1)
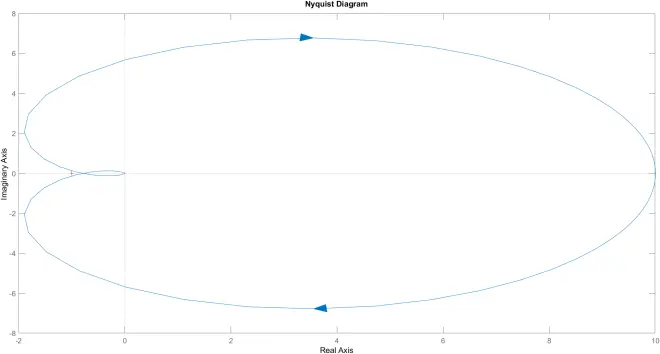
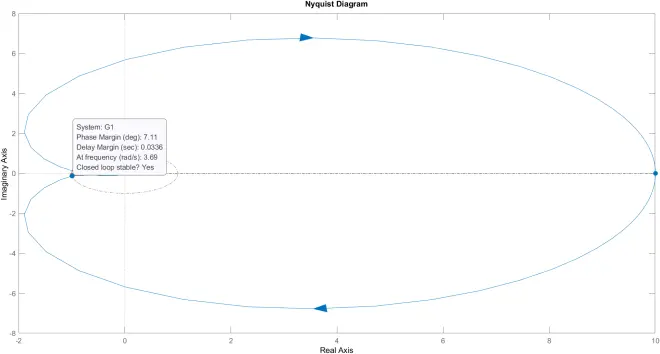
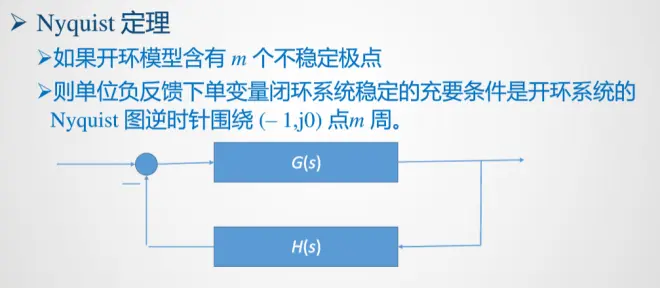
稳定
p = 0
Nyquist曲线不包含(-1,j 0)
k = 50
>> G2 = zpk([],[-1;-2;-5],2*5*50)
G2 =
500
-----------------
(s+1) (s+2) (s+5)
Continuous-time zero/pole/gain model.
>> nyquist(G2)
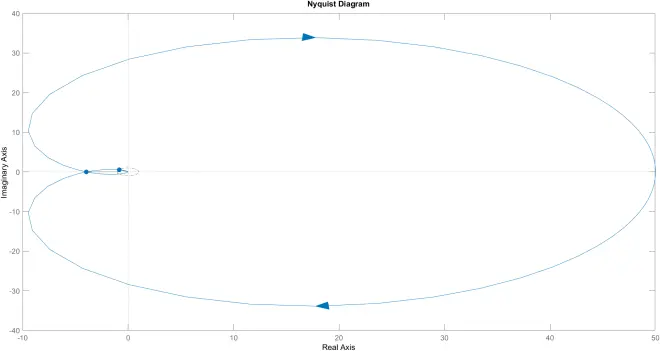
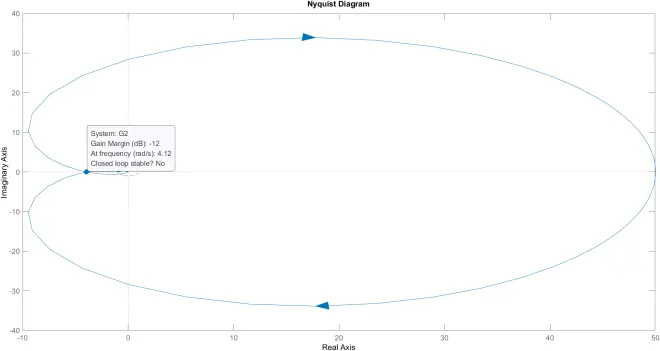
不稳定
p = 0
Nyquist图包围(-1,j0)一次

