【佟硕公益数学】-高考数学知识点盘点合集

一.排列组合的专题

1.

独立完成用+

不能用*

2.

3.原理性质: 从n个人里头选m个人出来的同时，自然就形成剩下的一个n-m人的小组

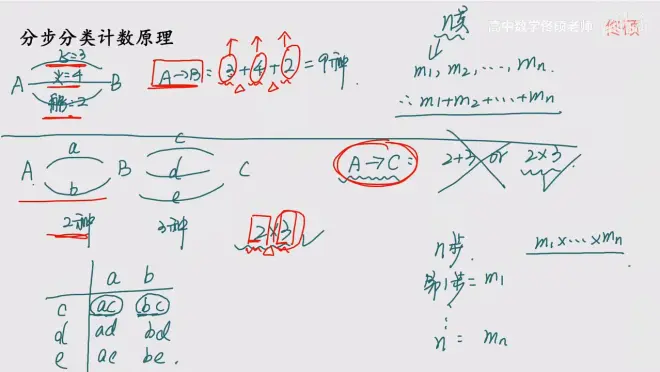
分布计数原理：做一个事情有多少个步骤，把每一个步骤方法写出来乘起来，就是完成整个事件的步骤和方法个数

分类计数原理：做这件事情，可以有很多种不同种类的方法，把每一种不同种类的方法，具体的方案个数写出来，加到一块

4.有顺序：排列

无顺序：组合

例1

信选箱子

例2

例3

例4

错误点：

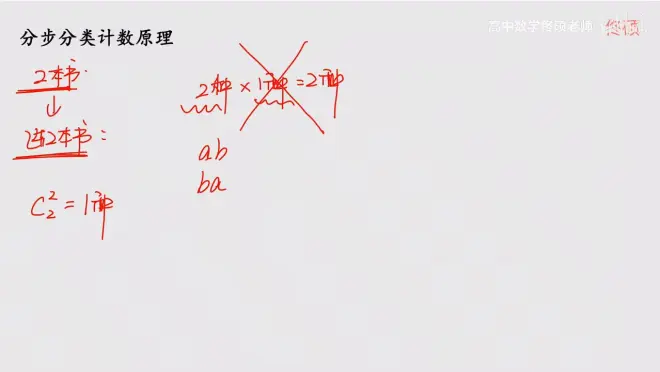
总结：1.思考完成这个事件如何做

2.分步骤（分大类）

二.

两种切入点：

1.人选位置：给这个人or那个人安排位置

2.位置选人：给这个位置or那个位置选人

例1

1.特殊元素优先安排

2.写到某步骤不确定，找到不确定的原因，针对这个原因回头分类

例2

例3

例4

三.

例1

例2

例3

四.

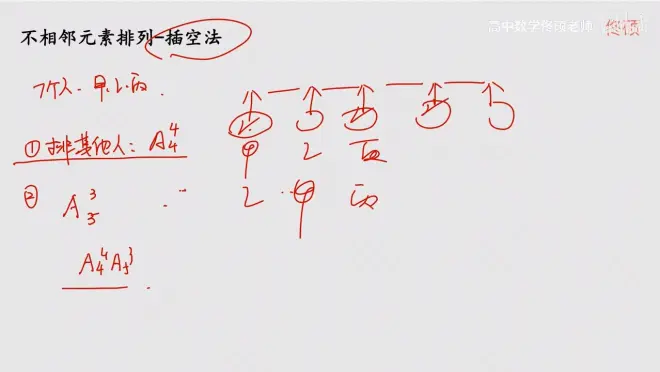
方法：

1.无要求的其他人排好

2.数下总共形成的空隙

3.把不相邻的几个人往空隙里头插入

例1

例2

例3

插入元素换位置是相同效果还是不同效果

五.

例1

方法：满足其中一个要求的所有方案当成总体

扣除不符合其中的方案

例2

例3

六.

只选不排

例1

例2

例3

例4

1.相同排在一起

2.不同的再排

例5

七.

一.圆锥曲线之直译法，定义法求轨迹方程

圆的概念:满足到一个定点，就是所谓的圆心的距离永远等于一个定长（半径），满足这些条件所组成的动点轨迹

例1

常考：

将常数项和常数项放一起，变量和变量放一起

变量 (带x的放一起) ，常数（不带x）

例1

例2

例3

例4

例5

例6

例7

三项和的展开式，配成一个完全平方

例8

例9

例1