【逻辑门的奇妙冒险】第3篇 造物的起点：与或非逻辑门

本篇目标：

1.理解与或非三个逻辑门的结构与特性；

在上一篇中，我们理解了CMOS管的特性，总结起来也就两个电路符号和两句话：

左图：X点高电平，AB导通；

右图：X点低电平，AB导通。

在本篇中，我们要理解的目标也就三个电路符号和三个表：

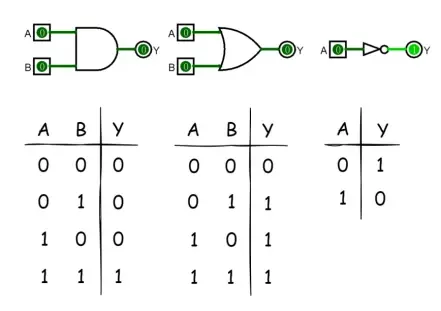
这三个电路符号分别叫做：与门、或门、非门。下面的三个表分别是这三个门对应的“真值表”。只要看懂了这仨电路符号和仨表，我们这一篇也就完事了。好，目标很明确，我们开始吧~

首先，我们先从最简单的非门开始，也就是最右边的那个图，只有一个输入一个输出。我们用上篇介绍的PMOS管和NMOS管各一个，搭建出以下结构：

图中的VDD表示高电平，谁和它连接了，谁就是“1”；GND是接地线，谁和它连接了，谁就是“0”。其中A点是输入，而Y点是输出。

简单分析一下，如果A点是高电平，那么根据CMOS管的特性，下面的N管导通，而P管截止，相当于Y点被连接到了GND上了，也即“A1则Y0”；相反，如果A点是低电平，那么对应的P管导通，N管截止，相当于Y点被连接到了VDD上了，也即“A0则Y1”。好勒，借助这个结构，我们就算完成了一次简单的取反运算，一个“叛逆的”“故意捣蛋的”电路。

这就是非门。它的电路符号是一个三角形末端一个圆圈，它的数学符号是“~”，它的真值表就两行，也就是下图的最右边（此图梅开二度，反复强调.jpg）：

接下来我们要用类似的手段，用CMOS管来搭建与门、或门。但是在这之前，我们可以回想一下中学学过的电路知识：并联和串联

左边是两个串联的开关，需要AB两个同时连接，电路才导通；右边是两个并联的开关，只要AB有一个连接，电路就导通。诶嘿，这个特性是不是和与门、或门的逻辑要求有些类似呢？我们注意到：与门要求，两个输入都是1，结果才是1，像不像串联电路呢？或门要求，两个输入只要有一个是1，结果就是1，像不像并联电路呢？

由此启发，我们可以这样摆弄我们的CMOS管，把与门电路的上半部分复制一份，然后并联一下；把下半部分也复制一份，但是串联一下，变成这个样子：

上边是两个并联的P管，下边是两个串联的N管。我们分析一下可以发现：如果AB都是1，那么下面俩N管导通，上面俩P管截止，Y就连接到GND上了，得到0；而AB只要有一个是0，则下面至少一个截止，上面至少一个导通，Y就连接到VDD上了，得到1。诶嘿，怎么跟我们想要的与门“AB都1才得到1”的逻辑相反了呀？怎么肥事？

没事，咱们不是已经有了非门了嘛，反了就反了，不怕，后面再接上一个非门就是了，于是电路就变成这样了：

我们再分析一下，AB两点都是1的时候，X点被连接到GND，得到0，同时X点后面连接这一个非门，又把X点的值反过来，Y点得到1；AB中任意一个是0的情况也符合预期。Nice，我们成功地用CMOS管搭建出了一个与门。它的电路符号是一个半圆，它的数学符号是“&”，它的真值表正是下图的最左边（此图反复梅开三度，反复强调.jpg）：

接下来的故事线就顺理成章了，似曾相识燕归来，我们同样对非门施展串联并联的把戏，这次是把上面的P管串联，把下面的N管并联，就变成了这样：

我们再分析一下，不出意外：当AB中有一个是1，下面并联的N管至少有一个导通，上面的P管至少有一个截止，则Y连接到了GND，得到0；当AB都是0时，下面的N管都是截止，上面的P管都是导通，则Y连接到了VDD，得到0。真巧，这个逻辑正好和非门相反。但是不慌，这次我们有经验了——来，给它上一个非门：

最后分析一通：只要AB有一个是1，则X点连接到GND，得到0，再被非门翻过来，得到1；只有AB都是0，X点才连接到VDD，得到1，最后再被非门翻过来，得到0。完美~我们成功用CMOS管搭建出了或门。它的电路符号是个月牙型，它的数学符号是“|”，它的真值表就是下图的中间部分（此图梅开四度，再次强调.jpg）：

这三个逻辑门，是数字电路的基础，是我们造物的起点。后期我们搭建出复杂的数字电路，包括中央处理器CPU，都是从这三个门开始的。因此，这三个门的逻辑非常重要，需要牢记。对此，笔者以前是这么记的，初学者可以参考，分享一下：

非门是“叛逆的”，给1得到0；

与门是“认真的”，全都是1才是1；

或门是“随便的”，只要有1就是1。

最后再看一眼这个图，很重要，要记住，梅开五度了属于是：

拓展阅读：

与、或、非三个门分别对应布尔代数里面的加法、乘法、取反。这三个门就已经是完备的了，也即，这三门的组合可以完成一切布尔代数的运算。而布尔代数和我们从小学习的一般数学运算，也就是加减乘除开方三角取对数等等等等是相通的。那些东西都可以变换成布尔代数里的加、乘、取反的组合。换言之，与或非三门，就可以完成四则运算开方三角取对数等等花里胡哨的运算，想想就很神奇，想想就很美妙！哇哦，与或非逻辑门，真是漂亮呀~

稍微有些不秒的是：与门、或门是冗余的！因为与门加上非门可以代替或门；或门加上与门也可以代替与门——非A与非B，再取反，就是A或B了；同样的，非A或非B，再取反，就是A与B了。也即，或门、非门，这俩就已经完备了；与门、非门，这俩也完备了，并不需要仨呀！坏了，与或非逻辑门，不漂亮了......

（前方高能，全是数学，欢迎靓仔来挑战）

更加不妙的是：随便一个“奇怪门”就可以完备了。什么是奇怪门，我们不妨先想想，二输入的逻辑门有几个呢？

二输入逻辑门的真值表也就4项，对应的输出都打上问号，我们直接穷举，也就16种逻辑门：

分析一下，我们可以发现：

1号门、16号门直接就是常量，没有用，辣鸡门；

4号门、6号门直接就是导线，没有用，废物门；

11号门、13号门直接就是非门，只有非门，肯定是不完备的；

2号门就是与门，它再加上非门，就完备啦；

8号门就是或门，它再加上非门，也完备啦；

7号门是有名字的，叫异或门，它就算加上非门，也不会完备；

10号门也是有名字，叫同或门，它就算加上非门，同样不会完备；

9号门是或非门，也就是或门再取反，可以抽象出非门，然后完备；

15号门是与非门，也即与门再取反，也可以抽象出非门，然后完备；

3号、5号、12号、14号门，没有名字，暂且统称为奇怪门，有趣的是，它们就算不加上非门，也是完备的；

例如：用3号奇怪门搭建一个非门，我们可以将A设定成常量1，这样一来，3号奇怪门就会变成单输入的，并且逻辑上等于取反B，好嘞，我们就得到一个基于奇怪门搭建的非门了。也即非B，等价于1 3 B。（注意红色的3是运算符）

接下来，我们用3号奇怪门搭建一个与门，先把B信号取反，我们不难发现：A与B，等价于A 3 非B。（注意红色的3是运算符）

诶嘿，非门、与门有了，或门也就组合一下，非A与非B，再取反就是或门了，于是乎，我们得到（注意红色的3是运算符）：

~B  = 1 3 B

A&B = A 3 ~B = A 3 (1 3 B)

A|B = ~(~A & ~B) = ~((1 3A) & (1 3 B)) = 1 3 ((1 3 A) 3 (1 3 (1 3 B))) 

真有意思，我们只用一个3号奇怪门，就可以完成与或非运算，完成布尔代数的加乘取反，进而完成四则运算开方三角取对数等等数学运算。更有意思的是，5号、12号、14号奇怪门都可以哦，构造方法类似，我就不再赘述了。

那为什么7号异或门、10号同或门无法完备呢？我们尝试了一下，确实无法构造出与或非等逻辑，但是要怎么证明它们不完备呢？这里就要有请抽象代数的群论登场了。笔者学艺不精，不会（流下了不学无术的泪水.jpg）

既然3、5、12、14都可以单门完备，难道不是更加简洁吗？与门、或门，都要配上非门才能完备，看起来差点意思呀？

其实，与门、或门（包括与非、或非）有特别特别好、特别特别重要的性质，就是结合律和交换律。回忆一下梅开五度的那个图和表，是不是AB对换位置也一样？而且再来一个C，先算AB还是先算BC也都一样？好像是的诶！好勒，基于此我们就可以定义出三输入的与门、或门：

相应的，3、5、12、14等奇怪门就没有办法定义三输入了，也没有交换律没有结合律，真是越琢磨越奇怪了，很不好办。这么一想，与门、或门有干净利索的三输入、可以交换可以结合。诶嘿，与或非逻辑门，又漂亮了呢！

最后预告一下，下一篇组合电路，内容量超级饱满哦~