关于函数近似的一些想法

本文主体内容不需要竞赛知识，只需要泰勒级数及其以下的常规数学知识即可。

up该学期在备考少创班。有了解的朋友或许知道，少创往年的物理试题常涉及硬开根号的计算，数值也是毫无取巧之处。而且不同于物理竞赛，少创禁止使用计算器。为此，up思考了如何手算（后来得知计算结果占的分值不大，考场上没人要去算的）当然，Taylor展开是我们最熟悉的方法，不过效率实在太低。下面主要讲讲up研究最深的一个想法。

我们只能直接计算加减乘除。因此对于一个函数f(x)，展开成为多项式，便可以使用加减乘计算。若想另辟蹊径，很容易想到引入除——分式。

首先将函数展开，从简单起见，只引入一个一次分式

再展开

由于构造的函数引入了n+3个参数，在最理想的情况下，它能达到n+2阶近似。对照系数可列方程组，并且容易求解

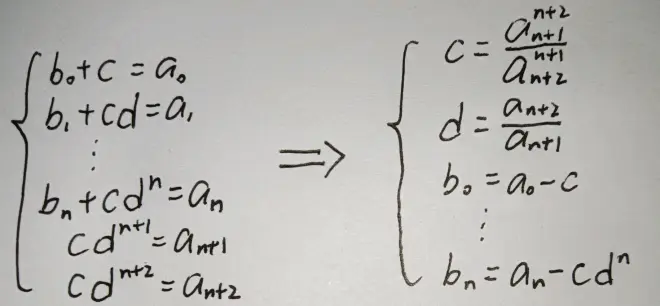
再代回函数，就行了

顺便写下余项

理论推导就差不多了，现在来具体试试效果。对于人工计算，其实高于一次都是比较麻烦的了，不妨就设n＝1，以√(1+x)为例算算吧

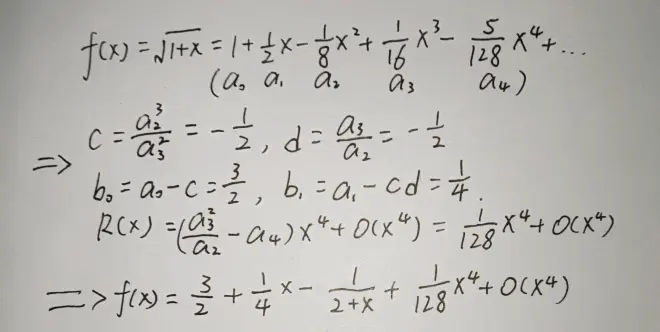
可以看到，只取前三项的话，精度已经比较高了。再具体算个数吧

对比一下√2的精确值：1.414213562373…误差为1.8×10^-9，和余项1.4÷49^4÷128差不多。相比之下，如果直接利用泰勒展开来计算，达到这个精度无疑是困难的。

有时间的读者不妨自己试试推导另外几个常见函数在这种方法下的近似式。没时间的话也没关系，up利用语文课的时间已经算好了：

自然，这些式子都是在x接近0时才能使用。那么，当x较大时怎么办呢？这其实也是很简单的问题啦。针对不同函数，解决方法不同，也请有兴趣的读者自行思考

此外，有种方法叫Pade逼近，这些式子应该都被囊括在这个方法里。但Pade逼近貌似是用计算机硬求导算的系数，鉴于我们这里考虑的是纯粹的手算方法，就不提了。如果说Pade逼近也有一套可以手算系数的方法的话，欢迎大家指出

好，下面进入二阶段。

如果想进一步增强近似程度，很容易想到引入两个一次分式或者一个二次分式。但如之前说的，手算二次比较麻烦了，因此这里考虑引入两个一次分式。但先概括一下：此时系数往往是极其无理的，并不有利于计算。只有少数函数可以采取这种方法

首先是类似的操作

对照系数，此时能达到n+4阶近似了

很明显，解这个方程组的突破口在于最后4个方程。这里就考验大家解方程的基本功了，有兴趣的读者可以先自己试试。下面给出up的过程

由③④很容易得到一个关于t的单变量方程，那么直接硬算下去就行了

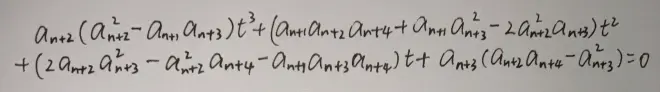
对于三次方程，我们是没什么办法的。不过你能注意到吗，这个方程一定有一个根：

舍去这个根后

从而能解出t。对于d，它自然也满足这个方程。也即t,d是这个方程的互异两根。（你可能会问：为什么不选择被舍弃的根？这是出于对称性考虑的，或者说追求数学的美感。而且，如果选择被舍去的根，近似效果会差些）

解出t,d后，也能轻易求出其他所有待定系数。但很明显，t,d很可能是无理数，此时其他系数将复杂无比。出于我们便于计算的目的，现在来考虑什么情况下存在有理解。

我们考虑常见的函数，即泰勒展开后的系数均为有理数。那么存在有理解就等价于Δ是平方数（这里的平方数包含有理数的平方）

接下来考虑具体的函数。又以√(1+x)为例吧

可以看到，通过上面的变形，规避了复杂的阶乘运算与通分，读者可以自行感受一下按照原始判别式的计算量。

我们最后得到了式子5(n+3)(2n+3)，我们暂且叫这种最简单的式子为“决定式”吧。只要决定式得到的为平方数，那么就能找到有理解了。至于决定式什么时候能得到平方数，经过分析后可以归结为数论中的双曲型方程（即pell方程的一般形式），up不擅长数论，不会解双曲型方程qwq

不过可以试验，当n=1,12,61…时，决定式都为平方数。但n不能太大，例如n=12，就要先写出12次的多项式，显然不符合便于计算的要求。因此我们只能取n=1。再来算算式子吧

又来算算√2

误差为4.7×10^-14，相当精确了。

其他函数的决定式怎样呢？up也算了一些↓

e^x：-(n+3)，显然无解

ln(1+x)：2(n+2)(n+3)，第一个解出现在n=6，太大不适合计算

³√(1+x)：7(n+3)(3n+5)，数论分析知无解

arctanx：2(2n+5)(2n+7)，模4知无解

sinx：有点复杂，大家自己算算吧(逃)

可以看到这个方法适用范围很窄。不过我们还能顺便拿来编编题，例如：

不知道怎么写结语，那就祝读到这里的朋友长生不老A.A