《漫画算法: 小灰的算法之旅》第4章 排序算法
引言
时间复杂度为O(n^2)的排序算法
冒牌排序、选择排序、插入排序、希尔排序(它的性能略优于O(n^2),但又比不上O(nlogn))
时间复杂度为O(nlogn)的排序算法
快速排序、归并排序、堆排序
时间复杂度为线性的排序算法
计数排序、桶排序、基数排序
排序算法还可以根据其稳定性,划分为稳定排序和不稳定排序
如果值相同的元素在排序后仍然保持着排序前的顺序,则这样的排序算法是稳定排序;
如果值相同的元素在排序后打乱了排序前的顺序,则这样的排序算法是不稳定排序

什么是冒泡排序
冒泡排序(bubble sort):是一种基础的交换排序



“漂”到了最右侧
冒泡排序的第1轮就结束了,以此类推,进行多轮冒泡

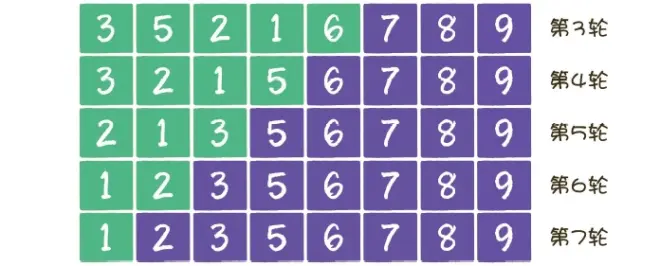
冒泡排序是一种稳定排序,值相等的元素并不会打乱原本的顺序。由于该排序算法的每一轮都要遍历所有元素,总共遍历(元素数量-1)轮,所以平均时间复杂度是O(n^2)
鸡尾酒排序
鸡尾酒排序的元素比较和交换过程是双向的。
举例:
[2, 3, 4, 5, 6, 7, 8, 1] 使用鸡尾酒排序法


在鸡尾酒排序的第3轮,需要重新从左向右比较并进行交换;
1和2比较,位置不变;
2和3比较,位置不变;
3和4比较,位置不变……
6和7比较,位置不变。
没有元素位置进行交换,证明已经有序,排序结束。
鸡尾酒排序的思路:排序过程就像钟摆一样,第1轮从左到右,第2轮从右到左,第3轮再从左到右……
鸡尾酒排序的优点是能够在特定条件下,减少排序的回合数;
而缺点也很明显,就是代码量几乎增加了1倍;
它能发挥出优势的场景,是大部分元素已经有序的情况
什么是快速排序
快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的;
冒泡排序在每一轮中只把1个元素冒泡到数列的一端,而快速排序则在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成两个部分


快速排序算法总体的平均时间复杂度是O(nlogn)
基准元素(pivot),在分治过程中,以基准元素为中心,把其他元素移动到它的左右两边
可以随机选择一个元素作为基准元素,并且让基准元素和数列首元素交换位置
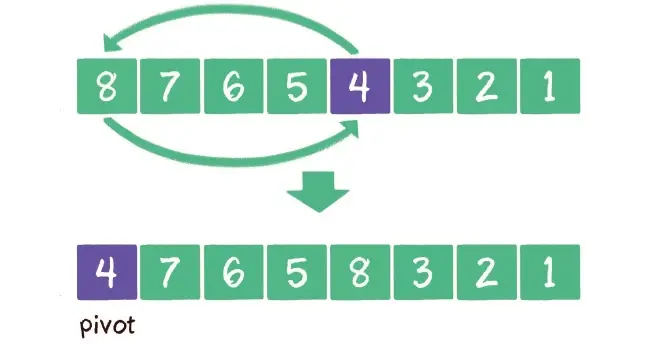
快速排序的平均时间复杂度是O(nlogn),最坏情况下的时间复杂度是O(n^2)
快速排序的实现方法:
双边循环法




向的元素进行交换。

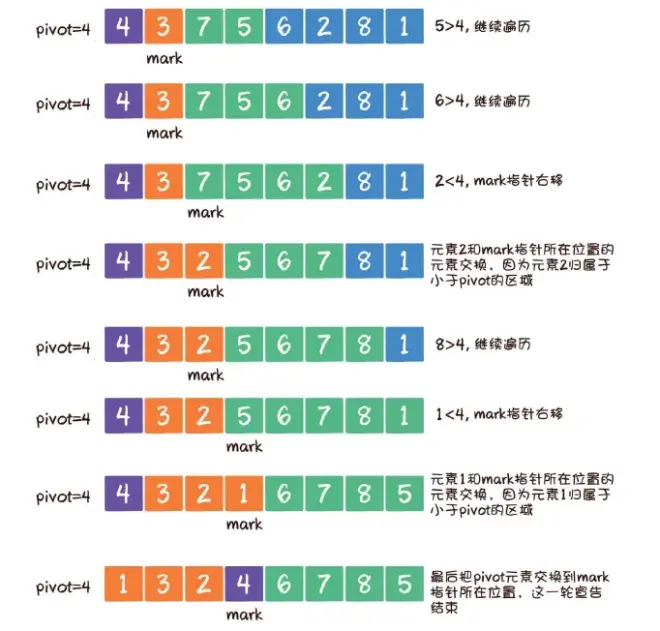
2.单边循环法


从基准元素的下一个位置开始遍历数组;
如果遍历到的元素大于基准元素,就继续往后遍历;
如果遍历到的元素小于基准元素,则需要做两件事:
第一,把mark指针右移1位,因为小于pivot的区域边界增大了1;
第二,让最新遍历到的元素和mark指针所在位置的元素交换位置,因为最新遍历的元素归属于小于pivot的区域



堆排序
堆排序算法:
把无序数组构建成二叉堆。需要从小到大排序,则构建成最大堆;需要从大到小排序,则构建成最小堆。
循环删除堆顶元素,替换到二叉堆的末尾,调整堆产生新的堆顶。
堆排序的时间复杂度为O(nlogn)
堆排序和快速排序的平均时间复杂度都是O(nlogn),并且都是不稳定排序;
至于不同点,快速排序的最坏时间复杂度是O(n^2),而堆排序的最坏时间复杂度稳定在O(nlogn);
快速排序递归和非递归方法的平均空间复杂度都是O(logn),而堆排序的空间复杂度是O(1)
计数排序和桶排序
[9,3,5,4,9,1,2,7,8,1,3,6,5,3,4,0,10,9,7,9] 20个随机整数



依此类推


优化版本的计数排序属于稳定排序
计数排序的时间复杂度
O(n+m)、空间复杂度为O(m)
计数排序的局限性:
当数列最大和最小值差距过大时,并不适合用计数排序
当数列元素不是整数时,也不适合用计数排序
桶排序
桶排序同样是一种线性时间的排序算法
每一个桶(bucket)代表一个区间范围
非整数列表: [4.5,0.84,3.25,2.18,0.5]




桶排序的总体时间复杂度为O(n);
至于空间复杂度就很容易得到了,同样是O(n)
小结


