专为“同构”这碟醋包的饺子（2022新高考Ⅰ导数）

解：（1）若，则与皆，

无最小值，不合题意.

当时，

，

令，得，

其单调性如下表所示：

故.

，

令，得；

其单调性如下表所示：

故.

依题意：，

即.

令，则

故，

故最多仅有一个零点，

又因为，故.

（2）由（1）可知

，，

，，

所以，

并且，

令，

当时，，

则与同属于区间，

因为在该区间，所以：

当，易知；

又因为

，

故存在唯一，使，

即，

即.

又因为：，

,

所以：，

.

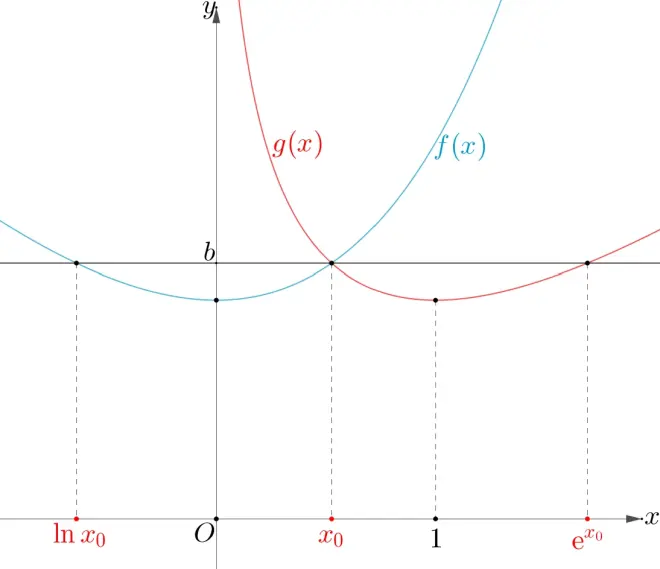
因为

故存在直线，其与两条曲线和共有三个不同的交点：、、，且.

即三个交点的横坐标成等差数列.