对欧拉恒等式严谨性的说明

序言
我脑海里想着这位十八世纪最伟大的数学家,雷奥哈德尔‧欧拉。我虽然对他一无所知,但手拿这个公式,我觉得自己可以感受到他的体温。他从这些看似毫无关系的数字中,发现了彼此之间自然的关联:
永无止境地循环下去的数字,和让人难以捉摸的虚数画出简洁的轨迹,在某一点落地。虽然没有圆的出现,但来自宇宙的
飘然地来到
的身旁,和害羞的
握着手。他们的身体紧紧地靠在一起,屏住呼吸,但有人加了
以后,世界就毫无预警地发生了巨大的变化。一却都归于
。
欧拉公式就像是暗夜中闪现的一道流星;也像是刻在漆黑的洞窟里的一行诗句。我被这个公式的美深深地打动了。
走下图书馆的楼梯时,我回头看了一下,数学书籍区仍然没有一个人影,一片寂静,没有人知道那里隐藏着多么美的事物。
——小川洋子《博士热爱的算式》
一 一个重要极限的证明
我之前写过一篇专栏——【专栏】欧拉公式exp(iπ)+1=0的7种“另类”证明,用于驳斥数学虚无主义者对欧拉恒等式的态度,然而由于我前期没有对这些虚无主义者做足准备工作,因此还是让这些虚无主义者挑到了刺。其中一个关键的问题,就是如何证明这个等价无穷小变换公式成立:
箭头右边其实是左边函数的幂级数展开的前两项。事实上,任何函数都可以用幂级数表示,包括不连续函数,这一点我会在后面说明。
你也许会问了:有时候,并不是只有整数次项,例如,如果只考虑0、1次项,这个半次项会被忽略,因此这些算法计算出来的结果未必可信。其实,这类担心duck不必:
显然,如果计算前没有事先考虑到半次项的存在,计算结果绝对会出大问题。这类计算方法,其实就是想用0次项表示非无穷小部分,用1次项表示无穷小部分。因此只要1次项有意义,结果就是可信的。
那么,下面我们就来证明吧!在证明过程中,为了保证严谨性,我不会改变乘方的原始定义——,以免虚无主义者又说这是我主观定义出来的结果。
那么问题来了,恒成立吗?
根据定义,我们可以将表示为:

我们也可以把表示为:

循环内的赋值不会改变变量“1的x次幂”的值,因此可以删去。这样,“重复执行x次”就成了空循环,也应该删去。简化后的程序如下:
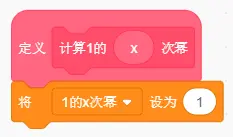
那么显然恒成立!
此时结果已经很明朗了:
至于负个(次)数、复个(次)数在日常生活中的意义,我们在第三节讨论。
二 欧拉公式的证明
参考资料:
【2】欧拉公式的多种证法(https://wenku.baidu.com/view/e32ff5047fd5360cbb1adb01.html)
由棣莫弗定理,得
三 复个(次)数在日常生活中的意义
参考资料:
【1】https://baike.baidu.com/item/闵可夫斯基空间
【2】从一到无穷大:科学中的事实和和臆测/【美】G.伽莫夫(Gamov,G.)著;暴永宁译.——修订版.——北京;科学出版社,2002(第66页)
【3】文盲正侃时间史、刘继军著.——南京:江苏人民出版社,2013.1(第262页)
【4】寻找薛定谔的猫/(英)格里宾著;张广才等译.——海口;海南出版社,2015.6(第103页)
此时,想必大家还对复个数没有概念,那么请大家思考一个问题:
问:如果一把尺子的长度有光秒(大约为地月距离),请问
把这样的尺子首尾相连,一共有多长?
答:首先我们要明确,一把光秒长的尺子,长度如下:
根据闵可夫斯基时空的距离公式(是空间坐标分量,
是时间坐标分量):
令,则
。
再令,则
因此,我们知道,与
等长,那么显然
把这样的尺子首尾相连,长度如下:
这个结果也够让你震惊一辈子了——把
光秒的、望不见尾的尺子首尾相连,一共仅有短短的
?!
你也许又会问了:把尺子的存在都是扯淡,谈何
把?
也许把尺子真的不存在吧,但至少我知道,反电子在量子力学中可以被当成负数个电子处理的,因此负数真的可以作为个数的!
那么复次数呢?其实也很好理解:

此时有没有可能是复数呢?绝对有可能!例如
就是一个最基本的例子。如果不承认这种可能性,无异于不承认复数。问题是闵氏时空必须要用复数来解释!复数是不可或缺的!
但这有个问题了——我们的一些同学,可能连负次数都没听说过,这时候要是讲复次数,可能会使他们因熬夜思考而猝死。那我就不得不先提一下负次数的概念了。首先,上过小学的人都知道,0除了代表没有,还可以代表起点(原点)。这样,0前面还有次数,那可是再正常不过的事了。
四 不连续函数也能用幂级数表示?
事实上,任何函数都可以用幂级数表示,包括不连续函数。例如以下函数:
当设置条件时,函数长这样:

当设置条件时,函数长这样:

当设置条件时,函数长这样:

当设置条件时,函数长这样:

当不限制的大小后,这个函数就变成了一个周期不连续函数,就像长城一样。然而它却是用幂级数定义的!注意:此处不能使用黎曼
函数进行计算,因为这样你只能得到
!(尽管
可导的时候确实为
,再求积分回去也确实是个常数)
重要的事情说三遍:
小伙伴们看完,一定要三连关注哟~
小伙伴们看完,一定要三连关注哟~


