郑涛（Tao Steven Zheng) 著

【问题】

《九章算术·勾股12》

【原文】今有户不知高、广，竿不知长短。横之不出四尺，从之不出二尺，邪之适出。问：户高、广、袤各几何？

【今译】假设有一门户，不知道它的高和广，有一根竹竿，不知道它的长短。将竹竿横着，有 4 尺出不去，竖起来有 2 尺出不去，将它斜着恰好能出门。问：门户的高、广、斜各是多少？

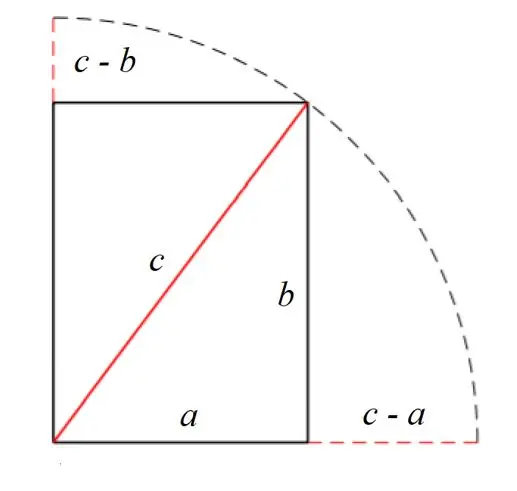
【题解】

设户广为勾 ，户高为股 ，户邪为弦 ，横不出为勾弦差 ，从不出为股弦差 。《九章算术》给的解法应用一个有趣的勾股公式：

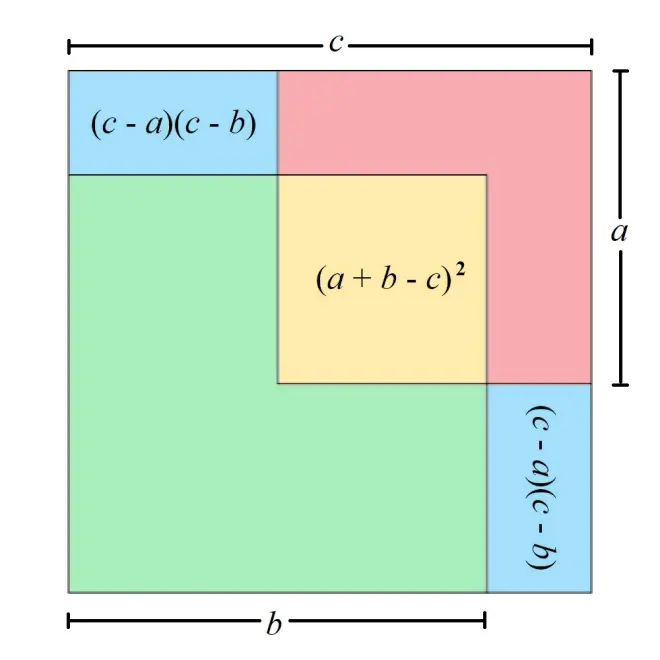
根据图 2，勾方的面积为 （红色），股方的面积为 （绿色），弦方的面积为 ；黄方部分为勾方和股方相重迭的正方形，其面积为 ；相对的两个青矩形的面积都是 。由图 2 可见

所以

根据勾股定理 ，得

开平方即得

户高

户广

户邪

户广 6 尺；户高 8 尺；户邪 10 尺（1 丈）。

《九章算术》的答案与解法

【原文】

答曰：广六尺，高八尺，袤一丈。

术曰：从、横不出相乘，倍，而开方除之。所得加从不出，即户广；加横不出，即户高，两不出加之，得户袤。

【今译】

答案：广是6尺，高是8尺，斜是1丈。

解法：将竖着、横着出不去的长度相乘，加倍，而对之开方除法。所得的结果加竖着出不去的长度，即是门户的广；加上横着出不去的长度，即是门户的高；加上两个出不去的长度，即得到门户的斜。