机器学习经典算法：时间序列ARIMA模型

ARIMA模型应用举例：

根据过去股价预测未来股价

根据过去降水量预测未来数据

现实数据一般都是弱平稳

“依赖性”举例:明天降水量和今天的有关

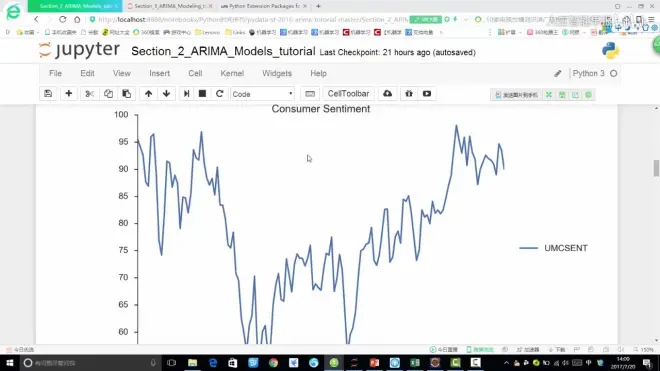
虽然横坐标以年为单位标记，但每两年（如05年和07年）之间是有24个月的数据的。

纵坐标：消费者信心指数

对一阶差分再进行一次差分，得到一阶差分和二阶差分

一阶差分平稳了一些

二阶差分更平稳了

（ARIMA步骤的第一步就是进行差分操作）

ARIMA=AR+I+MA

①AR：

p阶自回归过程：

阶数表示时间间隔的多少

1阶：表示今天和昨天的关系

2阶：表示今天和前天的关系

阶数的取值不能用肉眼看出来，后面会讲两个评估的方法

②MA：

AR+MA=ARMA

（当前值=基准值+过往值的加权平均+误差+过往误差的加权平均☆）

从自回归移动平均模型中看出，p（自回归模型阶数）和q（移动平均模型阶数）是我们需要指定其值的参数，γi和θi是我们要求解的参数。

③ARIMA中的I：指差分操作，含有需要指定其值的参数d。

ARIMA模型总的需要指定其值的参数为（p,d,q）

一般一阶差分就够了，很少做更高阶的差分

阶数：也叫滞后值

相关关系：[-1，1]

虚线：表示置信区间

横轴：阶数d 纵轴：ACF值

实现ARIMA的库：statamodels

用函数plot_acf()和plot_acpf()绘图

阴影表示置信区间

plot_acf()结果：

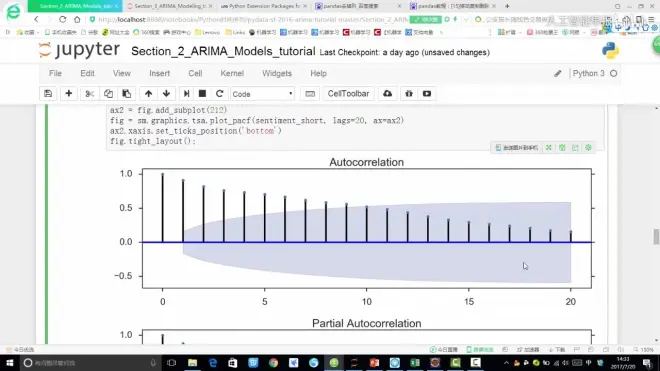
plot_acpf()结果：

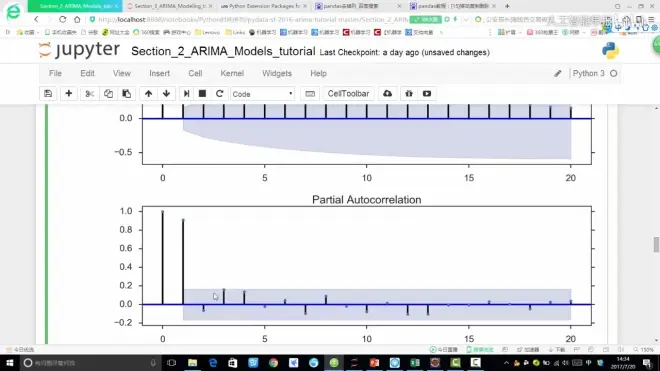
d:观察

p,q：通过plot_acf()和plot_pacf()的结果得到取值

对于AR模型，求p值看PACF图像。由图可知在2阶后进入置信区间（即截尾），所以该模型p值取2：

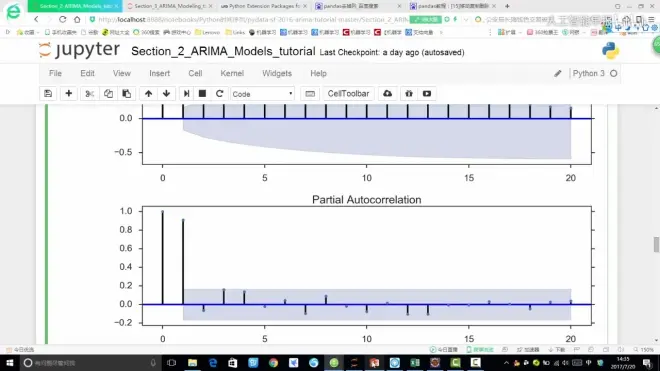
对于MA模型，求q值看ACF图像。由图可知也在2阶后进入置信区间（即截尾），所以该模型q值也取2：

☆ARIMA建模步骤：

①通过差分法将序列变得平稳，同时确定差分阶数（次数）d的值；

②通过函数plot_acf()和plot_pacf()绘制ACF（自相关函数，表示同一序列在不同时间点上的取值之间的相关性）和PACF（偏自相关函数，剔除了研究的两个时间点之间的点，对应的取值的影响）的图像，根据规则确定p和q的值；

③确定好d,p,q的值后， 直接使用statamodels调用ARIMA模型就可以了。

除了绘制ACF（自相关函数）和PACF（偏自相关函数），也可以通过绘制散点图，来可视化不同差分阶数d下，不同时间点对应值之间的相关性：

只看图可能还不太精准，可以通过遍历找到更精确的p和q的取值。

statamodels中有个SARIMAX函数，只需输入训练数据ts_train和p,d,q的值order(2,0,0)，就可以用fit()函数拟合模型：

然后通过遍历（从0到4），找到最优的p和q的值：

判断p和q取值好坏的是一个指标AIC/BIC（都是越低越好）：

qq图：看是不是一条直线 是，残差就符合正态分布