0基础上手【导数】全章知识/方法/原理！

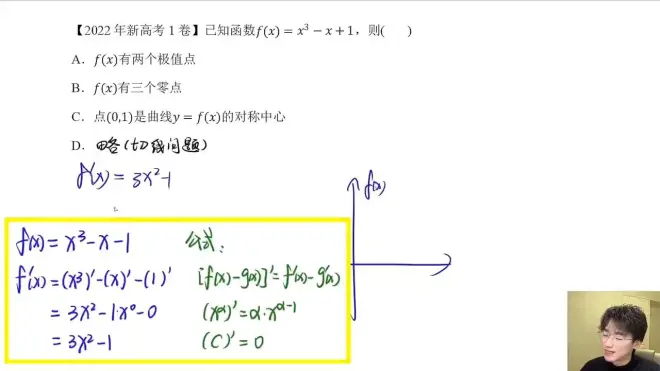
一.导数的含义：切线的斜率（f('x）=k)

该等式的含义就是x=x0时对应的切线的斜率（如下图x=1时的意义）

作用：1.切线问题 2.单调性的证明

切线问题核心：1.求切点 2.利用k=f'(x)求斜率

导数的基本运算：

切线问题的例题：

总结：对于过某点求切线的问题，第一步永远是利用k=f’（x）求出斜率，随后将x值带入f(x)中求出y。最后利用点斜式求出切线方程

例题2

2.单调性

核心：导函数的正负决定了原函数的增减性，即f'(x)∝f(x)

例题

导完后需要通过因式分解等方方法确定导函数的增减性，进而判断出原函数的增减性。同时，对于可以画出图的导数，则可以直接画图明确其增减性。

二.导函数与原函数图像的关系

例题

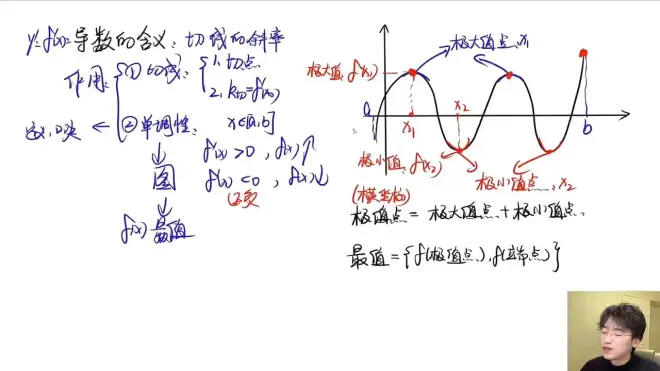
首先对原函数求导，画出导函数的图像

也就是说，原函数的增减性与导函数一致，同时原函数的增长或减小速率也与导函数相同

补充：极值点：由递减变为递增或递增变为递减的分界点叫做极值点

应用：在区间[a,b]中，函数的最值只会出现在端点或极值点的位置上

中等难度例题

例题2

三.多次求导

1.移项，构造函数

2.求导，寻找函数单调性

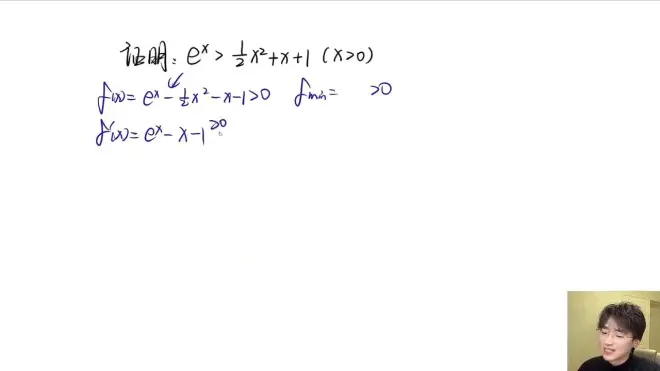
3.多次求导，直至可以运用图像证明其单调性

4.求出最终答案

总结：如果一个函数一次求导后仍然无法判断出导函数的单调性，则可以将导函数再次设为一个新函数并对其再次求导，直至可以判断单调性为止