郑涛 (Tao Steven Zheng) 著

【问题】

餐巾环问题（napkin ring problem）可以追溯到江户日本（Edo Japan）。日本数学家关孝和（Seki Kowa，1642-1708）最早用圆理（enri）的积分形决这个问题的人。关孝和把餐巾环形称为弧环体。

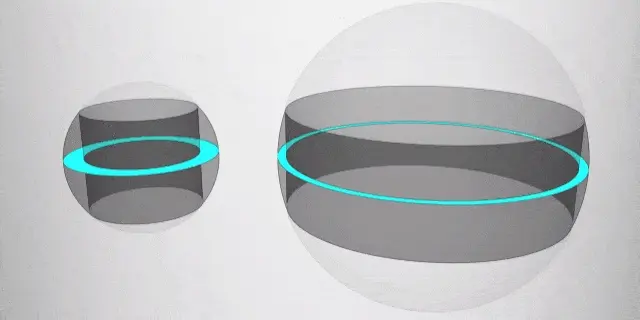
以下动画显示两个球体。各球体钻出了位于中心位置的圆柱体。剩下的立体形状称为餐巾环(napkin ring)。设球体的半径为 ，圆柱体的半径为 。求餐巾环的体积。

【题解】

用以下餐巾环的横截面图来分析。设球体的半径为 、圆柱孔的半径为 ，圆柱孔的半高为 。

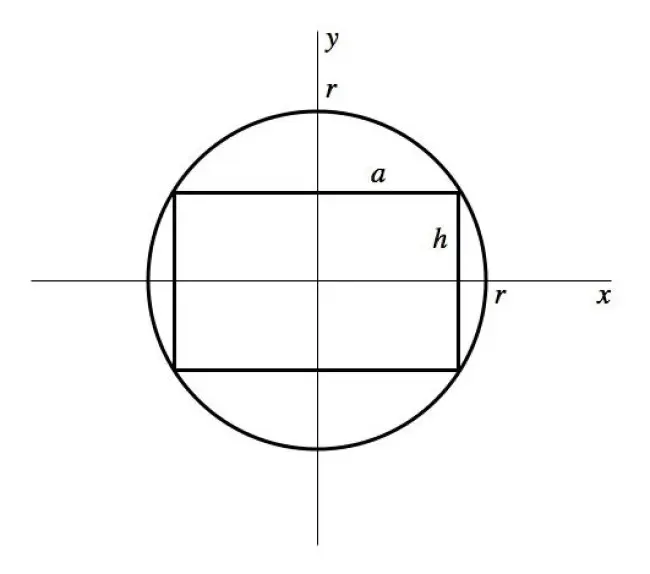
餐巾环等于球体（sphere）减去圆柱体（cylinder）减去两个球冠体（spherical cap）：

已知球体和圆柱体的体积（记得 是圆柱体的半高）：

还有这里

用积分法来推导球冠体的体积公式：

因此，餐巾环的体积是：

由于 ，得

以圆柱孔的高（）表示的餐巾环体积为：