控制系统仿真(MATLAB版)(三)
系统框图
谈到框图,首先不难联想到simulink基于模块化的系统仿真
首先我们来看一个simulink控制系统仿真



模块搭建好后,可以设置仿真时间、求解器以及步长
按下 Ctrl+E


clear
G1=tf(1,[1 1]);
G2=tf(1,[3 4 1]);
Gp=parallel(G1,G2); %系统并联部分的化简
G3=tf(1,[1 0]);
Gs=series(G3,Gp); %系统串联部分的化简
Gc=feedback(Gs,1) ; %系统负反馈连接
step(Gc,20)
如下图
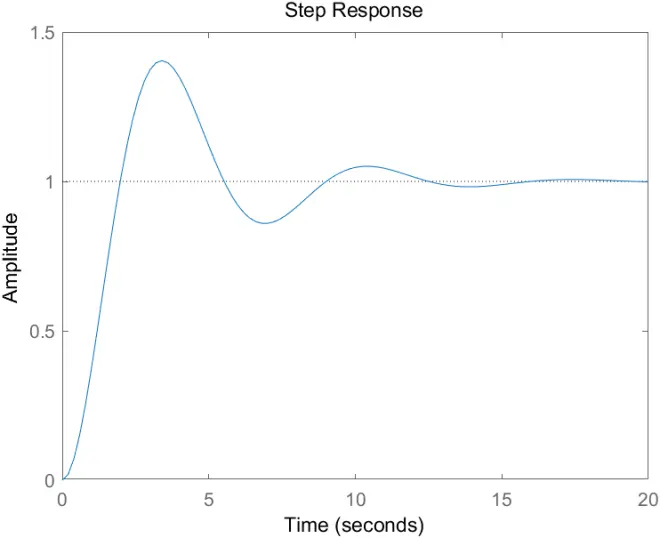
我们发现,matlab和simulink运行的结果一模一样
系统方框图
一、串联连接

matlab实现,可以实现多级串联
G = G2*G1;
G = series(G1,G2)
二、并联连接

在matlab中实现并联连接
G = G1+G2
G = parallel(G1,G2)
三、反馈连接





>> G1 = tf(1,[1 5 23]);
>> G2 = tf(1,[1 4]);
>> Gs = series(G1,G2)
Gs =
1
-----------------------
s^3 + 9 s^2 + 43 s + 92
Continuous-time transfer function.
>> Gs1 = G1*G2
Gs1 =
1
-----------------------
s^3 + 9 s^2 + 43 s + 92
Continuous-time transfer function.
>> Gp = parallel(G1,G2)
Gp =
s^2 + 6 s + 27
-----------------------
s^3 + 9 s^2 + 43 s + 92
Continuous-time transfer function.
>> Gp1 = G1+G2
Gp1 =
s^2 + 6 s + 27
-----------------------
s^3 + 9 s^2 + 43 s + 92
Continuous-time transfer function.
>> Gf = feedback(G1,G2,-1)
Gf =
s + 4
-----------------------
s^3 + 9 s^2 + 43 s + 93
Continuous-time transfer function.
>> Gf1 = feedback(G1,G2,1)
Gf1 =
s + 4
-----------------------
s^3 + 9 s^2 + 43 s + 91
Continuous-time transfer function.

