七夕节之婚姻问题升级版(feat.Wikipedia)*算了标题也争取下达到40字终于达到了nice！

2021-08-17 21:19 作者:浦东新区 0人读过 | 我要投稿

*这是编者在本文编辑的最后37个字，这是为了恰好达到30000个字的限制。

之前用秘书问题来指导找不到对象的各位找到好的另一半（使用37%法则），但还是不够，于是我花钱上Wikipedia找了升级版的秘书问题，相信各位能找到相爱的法则，即不是找到对象就是向往不了自由，谈不了恋爱，*不了狗，找不着对象。下次看到各位找到对象是在下次……这样的事情下次也不一定发生。[热词系列_对象][热词系列_不孤鸟][热词系列_对象]

好，

我们开始。（以下为 https://en.wikipedia.org/wiki/Secretary_problem 内容）

Secretary problem

秘书问题

From Wikipedia, the free encyclopedia 来自维基百科，免费的百科全书

Graphs of probabilities of getting the best candidate (red circles) from 得到最佳候选人(红圈)的概率图n Applications, and 申请，以及k/n (blue crosses) where (蓝色十字架)哪里k is the sample size 就是样本量

The secretary problem demonstrates a scenario involving optimal stopping theory[1][2] that is studied extensively in the fields of Applied probability, statistics, and decision theory. It is also known as the marriage problem, the sultan's dowry problem, the fussy suitor problem, the googol game, and the best choice problem.

秘书问题证明了一个包含最优停止理论[1][2]的场景，这个场景在应用概率论、统计学和决策理论中得到了广泛的研究。它也被称为婚姻问题，苏丹的嫁妆问题，挑剔的追求者问题，古格尔游戏，和最佳选择问题。

The basic form of the problem is the following: imagine an administrator who wants to hire the best secretary out of n{\displaystyle n} rankable Applicants for a position. The Applicants are interviewed one by one in random order. A decision about each particular Applicant is to be made immediately after the interview. Once rejected, an Applicant cannot be recalled. During the interview, the administrator gains information sufficient to rank the Applicant among all Applicants interviewed so far, but is unaware of the quality of yet unseen Applicants. The question is about the optimal strategy (stopping rule) to maximize the probability of selecting the best Applicant. If the decision can be deferred to the end, this can be solved by the simple maximum selection algorithm of tracking the running maximum (and who achieved it), and selecting the overall maximum at the end. The difficulty is that the decision must be made immediately.

这个问题的基本形式如下: 想象一下，一个管理人员想要从一个职位的 n 个可以确定的申请者中雇佣最好的秘书。申请人是按随机顺序逐一面试的。关于每个申请人的决定将在面试后立即作出。一旦被拒绝，申请人就不能被召回。在面试过程中，管理人员获得的信息足以将申请人列入到目前为止面试过的所有申请人之中，但不知道尚未见过的申请人的质量。问题是关于最优策略(停止规则) ，以最大限度地提高选择最佳申请人的概率。如果决策可以推迟到最后，这可以通过简单的最大值选择算法来解决，即跟踪运行的最大值(以及谁达到了最大值) ，并在最后选择总体最大值。困难在于必须立即作出决定。

The shortest rigorous proof known so far is provided by the odds algorithm. It implies that the optimal win probability is always at least $1/e$ {\displaystyle 1/e} (where e is the base of the natural logarithm), and that the latter holds even in a much greater generality. The optimal stopping rule prescribes always rejecting the first ∼n/e{\displaystyle \sim n/e} Applicants that are interviewed and then stopping at the first Applicant who is better than every Applicant interviewed so far (or continuing to the last Applicant if this never occurs). Sometimes this strategy is called the 1/e{\displaystyle 1/e} stopping rule, because the probability of stopping at the best Applicant with this strategy is about 1/e{\displaystyle 1/e} already for moderate values of n{\displaystyle n} . One reason why the secretary problem has received so much attention is that the optimal policy for the problem (the stopping rule) is simple and selects the single best candidate about 37% of the time, irrespective of whether there are 100 or 100 million Applicants.

迄今为止已知的最短的严格证明是由赔率算法提供的。这意味着最佳的胜算概率至少是1/e (e 是自然对数的基础) ，并且后者具有更大的普遍性。最佳停止规则规定总是拒绝第一个接受面试的申请人，然后在第一个比目前所有接受面试的申请人都要好的申请人面前停止(如果从未发生这种情况，则继续拒绝最后一个申请人)。有时这个策略被称为1/e 停止规则，因为对于 n 的中等值，这个策略在最佳应用程序上停止的概率已经是1/e 了。秘书问题之所以受到如此多的关注，其中一个原因是，解决这个问题的最佳策略(停止规则)很简单，在37% 的时间里选择最佳候选人，而不管申请者是1百还是1亿。

Formulation 配方

Although there are many variations, the basic problem can be stated as follows:

虽然有许多不同之处，但基本问题可以说明如下:

There is a single position to fill. 只有一个职位需要填补
There are 有n Applicants for the position, and the value of 申请这个职位的人，以及n is known. 众所周知
The Applicants, if seen altogether, can be ranked from best to worst unambiguously. 申请人，如果看到一起，可以排名从最好到最差毫不含糊
The Applicants are interviewed sequentially in random order, with each order being equally likely. 申请人按照随机顺序接受面试，每次面试的可能性都是相同的
Immediately after an interview, the interviewed Applicant is either accepted or rejected, and the decision is irrevocable. 面试结束后，面试申请人要么被接受，要么被拒绝，这个决定是不可撤销的
The decision to accept or reject an Applicant can be based only on the relative ranks of the Applicants interviewed so far. 接受或拒绝申请人的决定只能基于迄今为止所面试的申请人的相对级别
The objective of the general solution is to have the highest probability of selecting the best Applicant of the whole group. This is the same as maximizing the expected payoff, with payoff defined to be one for the best Applicant and zero otherwise. 一般解决方案的目标是在整个群体中选择最佳申请人的概率最高。这和最大化预期收益是一样的，最佳申请人的预期收益定义为1，否则为0

A candidate is defined as an Applicant who, when interviewed, is better than all the Applicants interviewed previously. Skip is used to mean "reject immediately after the interview". Since the objective in the problem is to select the single best Applicant, only candidates will be considered for acceptance. The "candidate" in this context corresponds to the concept of record in permutation.

一个候选人被定义为一个申请人谁，当面试，是比所有的申请人以前面试。Skip 的意思是“面试后立即拒绝”。由于问题的目标是选择单一的最佳申请人，只有候选人将被考虑接受。这个上下文中的“候选者”对应于排列中的记录的概念。

Deriving the optimal policy 推导最优策略

The optimal policy for the problem is a stopping rule. Under it, the interviewer rejects the first r − 1 Applicants (let Applicant M be the best Applicant among these r − 1 Applicants), and then selects the first subsequent Applicant that is better than Applicant M. It can be shown that the optimal strategy lies in this class of strategies.[citation needed] (Note that we should never choose an Applicant who is not the best we have seen so far, since they cannot be the best overall Applicant.) For an arbitrary cutoff r, the probability that the best Applicant is selected is

该问题的最优策略是一个停止规则。在这种情况下，面试官拒绝第一个 r-1申请人(让申请人 m 是这些 r-1申请人中最好的申请人) ，然后选择第一个后续的申请人优于申请人 m。结果表明，最优策略存在于这类策略中。[需要引证](注意，我们永远不应该选择一个不是我们迄今为止看到的最好的申请人，因为他们不可能是最好的整体申请人。)对于任意的截止值 r，选择最佳应用程序的概率为

$%20%20%20%20%7B%5Cdisplaystyle%20%7B%5Cbegin%7Baligned%7DP(r)%26%3D%5Csum%20_%7Bi%3D1%7D%5E%7Bn%7DP%5Cleft(%7B%5Ctext%7Bapplicant%20%7D%7Di%7B%5Ctext%7B%20is%20selected%7D%7D%5Ccap%20%7B%5Ctext%7Bapplicant%20%7D%7Di%7B%5Ctext%7B%20is%20the%20best%7D%7D%5Cright)%5C%5C%26%3D%5Csum%20_%7Bi%3D1%7D%5E%7Bn%7DP%5Cleft(%7B%5Ctext%7Bapplicant%20%7D%7Di%7B%5Ctext%7B%20is%20selected%7D%7D%7C%7B%5Ctext%7Bapplicant%20%7D%7Di%7B%5Ctext%7B%20is%20the%20best%7D%7D%5Cright)%5Ccdot%20P%5Cleft(%7B%5Ctext%7Bapplicant%20%7D%7Di%7B%5Ctext%7B%20is%20the%20best%7D%7D%5Cright)%5C%5C%26%3D%5Cleft%5B%5Csum%20_%7Bi%3D1%7D%5E%7Br-1%7D0%2B%5Csum%20_%7Bi%3Dr%7D%5E%7Bn%7DP%5Cleft(%5Cleft.%7B%5Cbegin%7Barray%7D%7Bl%7D%7B%5Ctext%7Bthe%20best%20of%20the%20first%20%7D%7Di-1%7B%5Ctext%7B%20applicants%7D%7D%5C%5C%7B%5Ctext%7Bis%20in%20the%20first%20%7D%7Dr-1%7B%5Ctext%7B%20applicants%7D%7D%5Cend%7Barray%7D%7D%5Cright%7C%7B%5Ctext%7Bapplicant%20%7D%7Di%7B%5Ctext%7B%20is%20the%20best%7D%7D%5Cright)%5Cright%5D%5Ccdot%20%7B%5Cfrac%20%7B1%7D%7Bn%7D%7D%5C%5C%26%3D%5Cleft%5B%5Csum%20_%7Bi%3Dr%7D%5E%7Bn%7D%7B%5Cfrac%20%7Br-1%7D%7Bi-1%7D%7D%5Cright%5D%5Ccdot%20%7B%5Cfrac%20%7B1%7D%7Bn%7D%7D%5Cquad%20%3D%5Cquad%20%7B%5Cfrac%20%7Br-1%7D%7Bn%7D%7D%5Csum%20_%7Bi%3Dr%7D%5E%7Bn%7D%7B%5Cfrac%20%7B1%7D%7Bi-1%7D%7D.%5Cend%7Baligned%7D%7D%7D%0A%0A$

The sum is not defined for r = 1, but in this case the only feasible policy is to select the first Applicant, and hence P(1) = 1/n. This sum is obtained by noting that if Applicant i is the best Applicant, then it is selected if and only if the best Applicant among the first i − 1 Applicants is among the first r − 1 Applicants that were rejected. Letting n tend to infinity, writing x {\displaystyle x} as the limit of (r-1)/n, using t for (i-1)/n and dt for 1/n, the sum can be Approximated by the integral

对于 r = 1没有定义总和，但是在这种情况下唯一可行的策略是选择第一个申请者，因此 p (1) = 1/n。如果申请人 i 是最佳申请人，那么只有当且仅当第一批 i-1申请人中的最佳申请人是第一批被拒绝的 r-1申请人之一时，才会选定这一总额。设 n 趋于无穷大，写 x 为(r-1)/n 的极限，用 t 表示(i-1)/n，dt 表示1/n，和可以用积分近似

$%20%20%20%20%7B%5Cdisplaystyle%20P(x)%3Dx%5Cint%20_%7Bx%7D%5E%7B1%7D%7B%5Cfrac%20%7B1%7D%7Bt%7D%7D%5C%2Cdt%3D-x%5Cln(x)%5C%3B.%7D%0A%0A$

Taking the derivative of P(x) with respect to x{\displaystyle x} , setting it to 0, and solving for x, we find that the optimal x is equal to 1/e. Thus, the optimal cutoff tends to n/e as n increases, and the best Applicant is selected with probability 1/e.

将 p (x)对 x 的导数设为0，求解 x，我们发现最优 x 等于1/e，因此，当 n 增大时，最优截止值趋于 n/e，最优选择的概率为1/e。

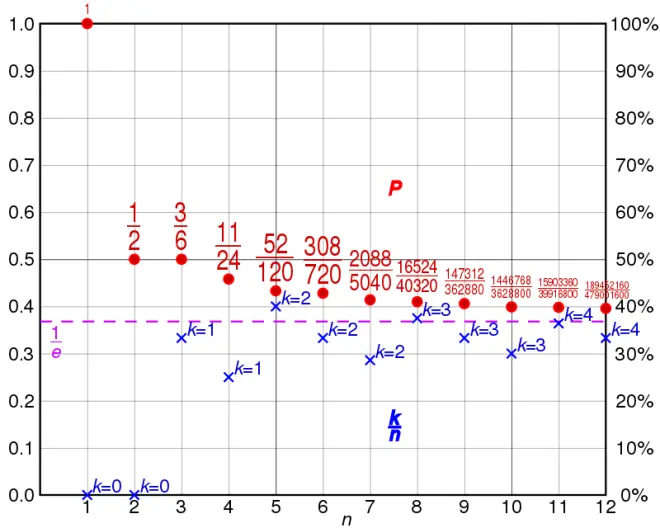
For small values of n, the optimal r can also be obtained by standard dynamic programming methods. The optimal thresholds r and probability of selecting the best alternative P for several values of n are shown in the following table.

对于 n 的小值，也可以用标准的动态规划方法得到最优 r。对于 n 的几个值，最佳阈值 r 和选择最佳替代 p 的概率如下表所示。

n 1 2 3 4 5 6 7 8 9

r 1 2 3 4 5 6 7 8 9

P 1.000 0.500 0.500 0.458 0.433 0.428 0.414 0.410 0.406

The probability of selecting the best Applicant in the classical secretary problem converges toward 1/e≈0.368{\displaystyle 1/e\Approx 0.368} .

在古典秘书问题中，选择最佳申请人的概率趋于1/e ≈0.368。

Alternative solution

This problem and several modifications can be solved (including the proof of optimality) in a straightforward manner by the odds algorithm, which also has other Applications. Modifications for the secretary problem that can be solved by this algorithm include random availabilities of Applicants, more general hypotheses for Applicants to be of interest to the decision maker, group interviews for Applicants, as well as certain models for a random number of Applicants.

Limitations 局限性

The solution of the secretary problem is only meaningful if it is justified to assume that the Applicants have no knowledge of the decision strategy employed, because early Applicants have no chance at all and may not show up otherwise.[citation needed]

秘书问题的解决只有在以下情况下才有意义: 申请人对所采用的决策策略一无所知，因为提前申请者根本没有机会，也可能不会出现。[需要引证]

One important drawback for Applications of the solution of the classical secretary problem is that the number of Applicants n{\displaystyle n} must be known in advance, which is rarely the case. One way to overcome this problem is to suppose that the number of Applicants is a random variable N{\displaystyle N} with a known distribution of $P(N%3Dk)_%7B%7Bk%3D1%2C2%2C%5Ccdots%20%7D%7D$ (Presman and Sonin, 1972). For this model, the optimal solution is in general much harder, however. Moreover, the optimal success probability is now no longer around 1/e but typically lower. This can be understood in the context of having a "price" to pay for not knowing the number of Applicants. However, in this model the price is high. Depending on the choice of the distribution of N{\displaystyle N} , the optimal win probability can Approach zero. Looking for ways to cope with this new problem led to a new model yielding the so-called 1/e-law of best choice.

解决传统秘书问题应用中的一个重要缺点是，必须事先知道申请人数 n，而这种情况很少发生。克服这个问题的一个方法是假设申请人数是一个随机变量 n，其分布是 p (n = k) k = 1,2，something (Presman and Sonin，1972)。然而，对于这个模型来说，最优解通常要困难得多。此外，最佳成功概率现在不再是1/e 左右，而是通常更低。这可以理解为，不知道申请人的数量就要付出”代价”。然而，在这个模型中，价格很高。根据 n 分布的选择，最优胜率可以接近于零。寻找应对这一新问题的方法，导致了一种新的模式，产生了所谓的最佳选择的1/e 法则。

1/e-law of best choice 1/e法则的最佳选择

The essence of the model is based on the idea that life is sequential and that real-world problems pose themselves in real time. Also, it is easier to estimate times in which specific events (arrivals of Applicants) should occur more frequently (if they do) than to estimate the distribution of the number of specific events which will occur. This idea led to the following Approach, the so-called unified Approach (1984):

这个模型的本质是基于这样一个观点，即生活是有序的，现实世界的问题是实时出现的。此外，比起估计将要发生的特定事件的数量分布，估计特定事件(申请人到达)应该更频繁发生的时间(如果发生的话)要容易得多。这一思想导致了以下的方法，即所谓的统一方法(1984年) :

The model is defined as follows: An Applicant must be selected on some time interval [0,T]{\displaystyle [0,T]} from an unknown number N{\displaystyle N} of rankable Applicants. The goal is to maximize the probability of selecting only the best under the hypothesis that all arrival orders of different ranks are equally likely. Suppose that all Applicants have the same, but independent to each other, arrival time density f{\displaystyle f} on [0,T]{\displaystyle [0,T]} and let F{\displaystyle F} denote the corresponding arrival time distribution function, that is

该模型的定义如下: 申请人必须在一定时间间隔[0，t ]从一个未知数 n 的可赎回的申请人中选出。目标是在假设不同等级的所有到达顺序都是相等的情况下，最大化只选择最佳的概率。假设所有申请人都具有相同但彼此独立的到达时间密度 f [0，t ] ，并且 f 表示相应的到达时间分布函数，即

$F(t)%3D%5Cint%20_%7B%7B0%7D%7D%5E%7B%7Bt%7D%7Df(s)ds$ , $%5C%2C0%5Cleq%20t%5Cleq%20T$ .

Let τ{\displaystyle \tau } be such that F(τ)=1/e.{\displaystyle F(\tau )=1/e.} Consider the strategy to wait and observe all Applicants up to time τ{\displaystyle \tau } and then to select, if possible, the first candidate after time τ{\displaystyle \tau } which is better than all preceding ones. Then this strategy, called 1/e-strategy, has the following properties:

设 τ 为 f (τ) = 1/e，考虑在 τ 之前等待并观察所有申请者的策略，如果可能的话，选择时间 τ 之后的第一个候选者，这个候选者优于之前的所有候选者。那么这个策略，称为1/e-strategy，有以下属性:

The 1/e-strategy

1/e 策略

(i) yields for all (i)所有人的收益N{\displaystyle N} { displaystyle n } a success probability of at least 1/e, 成功的概率至少是1/e,
(ii) is the unique strategy guaranteeing this lower success probability bound 1/e, and the bound is optimal, (ii)是保证这个较低成功概率上界1/e 的唯一策略，并且上界是最优的,
(iii) selects, if there is at least one Applicant, none at all with probability exactly 1/e. (iii)选择，如果至少有一名申请人，则没有任何一名申请人的概率恰好为1/e

The 1/e-law, proved in 1984 by F. Thomas Bruss, came as a surprise. The reason was that a value of about 1/e had been considered before as being out of reach in a model for unknown N{\displaystyle N} , whereas this value 1/e was now achieved as a lower bound for the success probability, and this in a model with arguably much weaker hypotheses (see e.g. Math. Reviews 85:m).

1984年，托马斯•布鲁斯(f. Thomas Bruss)证明了1/e 定律，这让人感到意外。原因是，在一个未知 n 的模型中，大约1/e 的值以前被认为是达不到的，而这个值1/e 现在是作为成功概率的一个下限而达到的，而这个下限在一个假设可能要弱得多的模型中(例如，数学)。评论85: m)。

The 1/e-law is sometimes confused with the solution for the classical secretary problem described above because of the similar role of the number 1/e. However, in the 1/e-law, this role is more general. The result is also stronger, since it holds for an unknown number of Applicants and since the model based on an arrival time distribution F is more tractable for Applications.

由于数字1/e 的作用相似，1/e 法有时会与上述经典秘书问题的解决方案相混淆。然而，在1/e 法中，这种作用更为一般。这个结果也更有说服力，因为它适用于未知数量的申请者，而且基于到达时间分布的模型对于应用程序来说更易于处理。

The game of googol 古戈尔的游戏

According to Ferguson(1989)[1], the secretary problem Appeared for the first time in print when it was featured by Martin Gardner in his February 1960 Mathematical Games column in Scientific American.[1] Here is how Gardner 1966 formulated it: "Ask someone to take as many slips of paper as he pleases, and on each slip write a different positive number. The numbers may range from small fractions of 1 to a number the size of a googol (1 followed by a hundred zeroes) or even larger. These slips are turned face down and shuffled over the top of a table. One at a time you turn the slips face up. The aim is to stop turning when you come to the number that you guess to be the largest of the series. You cannot go back and pick a previously turned slip. If you turn over all the slips, then of course you must pick the last one turned."

根据 Ferguson (1989)[1]的说法，秘书问题在1960年2月 Martin Gardner 在《科学美国人》的数学游戏专栏中首次出现。[1]加德纳1966年是这样阐述的: “让某人随心所欲地拿纸条，并在每张纸条上写上不同的正数。这些数字可以是1的小分数，也可以是10的100次方（1后面100个0，巨大的数字），甚至更大。这些纸条正面朝下，拖曳在桌面上。一次一个，你把纸条正面朝上。这样做的目的是当你到达一个数字时停止转动，你猜这个数字是这个系列中最大的。你不能回到过去，拿一张之前翻过的纸条。如果你把所有的纸条都翻过来，那么当然你必须把最后一张翻过来。”

In the article "Who solved the Secretary problem?" Ferguson(1989)[1] pointed out that the secretary problem remained unsolved as it was stated by M. Gardner, that is as a two-person zero-sum game with two antagonistic players. In this game Alice, the informed player, writes secretly distinct numbers on n{\displaystyle n} cards. Bob, the stopping player, observes the actual values and can stop turning cards whenever he wants, winning if the last card turned has the overall maximal number. The difference with the basic secretary problem is that Bob observes the actual values written on the cards, which he can use in his decision procedures. The numbers on cards are Analogous to the numerical qualities of Applicants in some versions of the secretary problem. The joint probability distribution of the numbers is under the control of Alice.

在文章“谁解决了秘书问题?”弗格森(1989) [1]指出，秘书问题仍然没有解决，因为它是由加德纳说，这是一个两人零和对策，两个敌对的参与者。在这个游戏中，知情的玩家爱丽丝在 n 张卡片上秘密写下不同的数字。停牌玩家鲍勃观察实际数值，可以随时停止翻牌，如果最后一张牌翻出的牌总数最大，他就赢。基本秘书问题的不同之处在于鲍勃观察卡片上写的实际价值，这些价值可以用于他的决策过程。卡片上的数字类似于秘书问题的某些版本中申请者的数字质量。数字的联合分布在 Alice 的控制之下。

Bob wants to guess the maximal number with the highest possible probability, while Alice's goal is to keep this probability as low as possible. It is not optimal for Alice to sample the numbers independently from some fixed distribution, and she can play better by choosing random numbers in some dependent way. For n=2{\displaystyle n=2} Alice has no minimax strategy, which is closely related to a paradox of T. Cover. But for n>2{\displaystyle n>2} the game has a solution: Alice can choose random numbers (which are dependent random variables) in such a way that Bob cannot play better than using the classical stopping strategy based on the relative ranks (Gnedin 1994).

鲍勃想用最高的概率来猜测最大的数字，而爱丽丝的目标是尽可能保持最低的概率。对于爱丽丝来说，独立于某个固定分布的数字样本并不是最优的，她可以通过某种相关的方式选择随机数来发挥更好的作用。对于 n = 2，Alice 没有极大极小策略，这与 t. Cover 悖论密切相关。但是对于 n > 2，游戏有一个解决方案: Alice 可以选择随机数(相依随机变量) ，这样 Bob 就不能比使用基于相对等级的经典停止策略玩得更好(Gnedin 1994)。

Heuristic performance 启发式性能

The remainder of the article deals again with the secretary problem for a known number of Applicants.

文章的其余部分再次涉及已知数量的申请人的秘书问题。

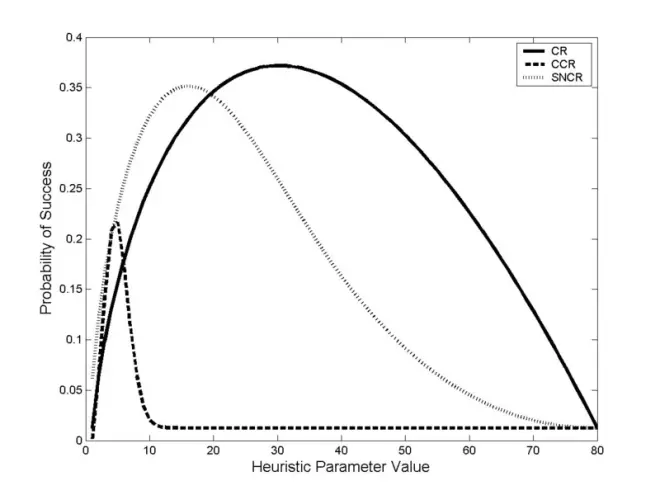
Expected success probabilities for three heuristics. 三种启发式的预期成功概率

Stein, Seale & Rapoport 2003 derived the expected success probabilities for several psychologically plausible heuristics that might be employed in the secretary problem. The heuristics they examined were:

2003年，Stein，Seale & Rapoport 推导出了几种可能用于秘书问题的心理学上合理的启发式方法的预期成功概率。他们调查的启发式问题是:

The cutoff rule (CR): Do not accept any of the first 截止规则(CR) : 不要接受任何第一个y Applicants; thereafter, select the first encountered candidate (i.e., an Applicant with relative rank 1). This rule has as a special case the optimal policy for the classical secretary problem for which 然后，选择第一个遇到的候选人(即相对职级1的申请人)。该规则作为一个特例，对于经典的秘书问题具有最优策略y = r.
Candidate count rule (CCR): Select the 候选人计数规则(CCR) : 选择y-th encountered candidate. Note, that this rule does not necessarily skip any Applicants; it only considers how many candidates have been observed, not how deep the decision maker is in the Applicant sequence. 遇到的候选人。请注意，这条规则并不一定忽略任何申请人; 它只考虑有多少候选人被遵守，而不考虑决策者在申请人序列中的深度
Successive non-candidate rule (SNCR): Select the first encountered candidate after observing 连续非候选规则(SNCR) : 在观察后选择第一个遇到的候选者y non-candidates (i.e., Applicants with relative rank > 1). 非候选人(即相对职级 > 1的申请人)

Each heuristic has a single parameter y. The figure (shown on right) displays the expected success probabilities for each heuristic as a function of y for problems with n = 80.

每种启发式方法都有一个参数 y。该图(如右图所示)显示了对于 n = 80的问题，每个启发式算法的预期成功概率作为 y 的函数。

Cardinal payoff variant 基数回报变量

Finding the single best Applicant might seem like a rather strict objective. One can imagine that the interviewer would rather hire a higher-valued Applicant than a lower-valued one, and not only be concerned with getting the best. That is, the interviewer will derive some value from selecting an Applicant that is not necessarily the best, and the derived value increases with the value of the one selected.

找到一个最好的申请人似乎是一个相当严格的目标。我们可以想象，面试官宁愿雇佣一个价值较高的应聘者，也不愿雇佣一个价值较低的应聘者，而且不仅仅关心如何得到最好的应聘者。也就是说，面试官会从选择一个不一定是最好的应聘者中得到一些价值，并且得到的价值会随着被选中的应聘者的价值而增加。

To model this problem, suppose that the n{\displaystyle n} Applicants have "true" values that are random variables X drawn i.i.d. from a uniform distribution on [0, 1]. Similar to the classical problem described above, the interviewer only observes whether each Applicant is the best so far (a candidate), must accept or reject each on the spot, and must accept the last one if he/she is reached. (To be clear, the interviewer does not learn the actual relative rank of each Applicant. He/she learns only whether the Applicant has relative rank 1.) However, in this version the payoff is given by the true value of the selected Applicant. For example, if he/she selects an Applicant whose true value is 0.8, then he/she will earn 0.8. The interviewer's objective is to maximize the expected value of the selected Applicant.

为了对这个问题进行建模，假设 n 个申请人的“真”值是随机变量 x 从[0,1]上的均匀分布中抽取的 i.i.i.i.d. 。与上面描述的经典问题类似，面试官只是观察每个应聘者是否是目前为止最好的(候选人) ，必须当场接受或拒绝每个人，如果他/她被录取，必须接受最后一个人。(需要说明的是，面试官并不知道每个应聘者的实际相对排名。他/她只知道申请人是否有相对等级1。)然而，在这个版本中，回报是由被选中的申请人的真实价值决定的。例如，如果他/她选择一个真实值为0.8的申请人，那么他/她将获得0.8。面试官的目标是最大化被选中的应聘者的期望价值。

Since the Applicant's values are i.i.d. draws from a uniform distribution on [0, 1], the expected value of the tth Applicant given that $x_%7B%7Bt%7D%7D%3D%5Cmax%20%5Cleft%5C%7Bx_%7B1%7D%2Cx_%7B2%7D%2C%5Cldots%20%2Cx_%7Bt%7D%5Cright%5C%7D$ is given by

由于申请人的值是从[0,1]上的均匀分布中得到的 i.i.i.d，所以在 xt = max { x1，x2，... ，xt }的情况下，tth（第t个）申请人的期望值是由

$%20%20%20%20E_%7B%7Bt%7D%7D%3DE%5Cleft(X_%7B%7Bt%7D%7D%7CI_%7B%7Bt%7D%7D%3D1%5Cright)%3D%7B%5Cfrac%20%7Bt%7D%7Bt%2B1%7D%7D.%0A%0A$

As in the classical problem, the optimal policy is given by a threshold, which for this problem we will denote by c{\displaystyle c} , at which the interviewer should begin accepting candidates. Bearden 2006 showed that c is either $%7B%5Cdisplaystyle%20%5Clfloor%20%7B%5Csqrt%20%7Bn%7D%7D%5Crfloor%20%7D$ or $%5Clceil%20%7B%5Csqrt%20n%7D%5Crceil%20$ . (In fact, whichever is closest to $%7B%5Csqrt%20n%7D$ .) This follows from the fact that given a problem with n{\displaystyle n} Applicants, the expected payoff for some arbitrary threshold 1≤c≤n{\displaystyle 1\leq c\leq n} is

在经典问题中，最优策略由一个阈值给出，对于这个问题，我们将用 c 表示，从这个阈值开始，面试官应该开始接受候选人。Bearden 2006年的研究表明，c 要么是“根号n向下取整”，要么是“根号n向上取整”。(事实上，无论哪个最接近 n。)这源于这样一个事实，即给定一个有 n 个申请人的问题，某个任意阈值1≤ c ≤ n 的预期收益是

$%20V_%7B%7Bn%7D%7D(c)%3D%5Csum%20_%7B%7Bt%3Dc%7D%7D%5E%7B%7Bn-1%7D%7D%5Cleft%5B%5Cprod%20_%7B%7Bs%3Dc%7D%7D%5E%7B%7Bt-1%7D%7D%5Cleft(%7B%5Cfrac%20%7Bs-1%7D%7Bs%7D%7D%5Cright)%5Cright%5D%5Cleft(%7B%5Cfrac%20%7B1%7D%7Bt%2B1%7D%7D%5Cright)%2B%5Cleft%5B%5Cprod%20_%7B%7Bs%3Dc%7D%7D%5E%7B%7Bn-1%7D%7D%5Cleft(%7B%5Cfrac%20%7Bs-1%7D%7Bs%7D%7D%5Cright)%5Cright%5D%7B%5Cfrac%20%7B1%7D%7B2%7D%7D%3D%7B%7B%5Cfrac%20%7B2cn-%7Bc%7D%5E%7B%7B2%7D%7D%2Bc-n%7D%7B2cn%7D%7D%7D.$

Differentiating Vn(c){\displaystyle V_{n}(c)} with respect to c, one gets

关于 c 的微分式 Vn (c) ，得到

$%7B%5Cfrac%20%7B%5Cpartial%20V%7D%7B%5Cpartial%20c%7D%7D%3D%7B%5Cfrac%20%7B-%7Bc%7D%5E%7B%7B%5C%2C2%7D%7D%2Bn%7D%7B2%7Bc%7D%5E%7B%7B%5C%2C2%7D%7Dn%7D%7D.$

Learning in the partial-information sequential search paradigm. The numbers display the expected values of Applicants based on their relative rank (out of m total Applicants seen so far) at various points in the search. Expectations are calculated based on the case when their values are uniformly distributed between 0 and 1. Relative rank information allows the interviewer to more finely evaluate Applicants as they accumulate more data points to compare them to. 部分信息/线性搜索范式下的学习。这些数字显示了申请人在搜索过程中各个点上的相对排名(迄今为止，总共有万申请人)的预期价值。期望值是根据它们的值均匀分布在0到1之间的情况计算出来的。相对排名信息允许面试官更好地评估应聘者，因为他们积累了更多的数据点来比较他们

Since $%5Cpartial%20%5E%7B%7B%5C%2C2%7D%7DV%2F%5Cpartial%20c%5E%7B%7B%5C%2C2%7D%7D%3C0$ for all permissible values of c{\displaystyle c} , we find that V{\displaystyle V} is maximized at $c%3D%7B%5Csqrt%20n%7D$ . Since V is convex in c{\displaystyle c} , the optimal integer-valued threshold must be either $%5Clfloor%20%7B%5Csqrt%20n%7D%5Crfloor%20$ or $%7B%5Cdisplaystyle%20%5Clceil%20%7B%5Csqrt%20%7Bn%7D%7D%5Crceil%20%7D$ . Thus, for most values of n{\displaystyle n} the interviewer will begin accepting Applicants sooner in the cardinal payoff version than in the classical version where the objective is to select the single best Applicant. Note that this is not an asymptotic result: It holds for all n{\displaystyle n} . However, this is not the optimal policy to maximize expected value from a known distribution. In the case of a known distribution, optimal play can be calculated via dynamic programming.

由于对于所有 c 的许可标准均采用∂2V/∂c2 < 0，我们发现在 c = n 时 v 最大。因为 v 在 c 中是凸的，所以最佳整数值阈值必须是 “根号n向下取整” 或 “根号n向上取整”。因此，对于 n 的大多数值，面试官在基本支付版本中开始接受应聘者的时间要比在传统版本中开始接受应聘者的时间要短，传统版本的目标是选择最好的应聘者。注意这不是一个渐近结果: 它适用于所有的 n。然而，这不是从已知分布最大化期望值的最优策略。在已知分布的情况下，最佳发挥可以通过动态规划计算。

A more general form of this problem introduced by Palley and Kremer (2014)[3] assumes that as each new Applicant arrives, the interviewer observes their rank relative to all of the Applicants that have been observed previously. This model is consistent with the notion of an interviewer learning as they continue the search process by accumulating a set of past data points that they can use to evaluate new candidates as they arrive. A benefit of this so-called partial-information model is that decisions and outcomes achieved given the relative rank information can be directly compared to the corresponding optimal decisions and outcomes if the interviewer had been given full information about the value of each Applicant. This full-information problem, in which Applicants are drawn independently from a known distribution and the interviewer seeks to maximize the expected value of the Applicant selected, was originally solved by Moser (1956),[4] Sakaguchi (1961),[5] and Karlin (1962).

Palley 和 Kremer (2014)[3]提出了这个问题的一个更普遍的形式，假设每一个新的申请者到来时，面试官都会观察他们相对于之前所观察到的所有申请者的排名。这个模型符合面试官在继续搜索过程中学习的概念，通过积累一系列过去的数据点，他们可以用这些数据点来评估新的应聘者。这种所谓的部分信息模型的一个好处是，如果面试官获得了关于每个申请人价值的全部信息，那么根据相对排名信息所作出的决定和取得的结果可以直接与相应的最佳决定和结果进行比较。这个完全信息问题是由 Moser (1956) ，Sakaguchi (1961) ，[5]和 Karlin (1962)最初解决的。

Other modifications 其他修订

There are several variants of the secretary problem that also have simple and elegant solutions.

秘书问题有几种变体，也有简单而优雅的解决方案。

One variant replaces the desire to pick the best with the desire to pick the second-best.[6][7][8] Robert J. Vanderbei calls this the "postdoc" problem arguing that the "best" will go to Harvard. For this problem, the probability of success for an even number of Applicants is exactly $%7B%5Cfrac%20%7B0.25n%5E%7B2%7D%7D%7Bn(n-1)%7D%7D$ . This probability tends to 1/4 as n tends to infinity illustrating the fact that it is easier to pick the best than the second-best.

一种变体取代了选择最好的人的愿望，取而代之的是选择次好的人。罗伯特 · j · 范德贝把这个问题称为“博士后”问题，他认为“最好的”应该去哈佛。对于这个问题，偶数申请者成功的概率正好是0.25 n2n (n-1)。这个概率趋向于1/4，因为 n 趋向于无穷大，这说明选择最好的比选择次好的容易。

For a second variant, the number of selections is specified to be greater than one. In other words, the interviewer is not hiring just one secretary but rather is, say, admitting a class of students from an Applicant pool. Under the assumption that success is achieved if and only if all the selected candidates are superior to all of the not-selected candidates, it is again a problem that can be solved. It was shown in Vanderbei 1980 that when n is even and the desire is to select exactly half the candidates, the optimal strategy yields a success probability of $%7B%5Cfrac%20%7B1%7D%7Bn%2F2%2B1%7D%7D$ .

对于第二个变体，选择的数目被指定为大于一。换句话说，面试官不是只雇佣一个秘书，而是从应聘者中录取一类学生。假定只有当且仅当所有被选中的候选人都优于所有未被选中的候选人时，才能取得成功，这又是一个可以解决的问题。Vanderbei 1980年的研究表明，当 n 为偶数且希望选出正好一半的候选者时，最优策略产生1 n/2 + 1的成功概率。

Another variant is that of selecting the best k{\displaystyle k} secretaries out of a pool of n{\displaystyle n} , again in an on-line algorithm. This leads to a strategy related to the classic one and cutoff threshold of $%7B%5Cfrac%20%7B0.25n%5E%7B2%7D%7D%7Bn(n-1)%7D%7D$ for which the classic problem is a special case Ghirdar 2009.

另一种变体是从 n 个秘书池中选择最好的 k 个秘书，同样是在联机算法中。这导致了一个与经典的策略和0.25 n2/n (n-1)的临界阈值相关的经典问题是一个特例 Ghirdar 2009。

Multiple choice problem 多项选择题

A player is allowed r{\displaystyle r} choices, and he wins if any choice is the best.Gilbert & Mosteller 1966 showed that an optimal strategy is given by a threshold strategy (cutoff strategy). An optimal strategy belongs to the class of strategies defined by a set of threshold numbers $%7B%5Cdisplaystyle%20(a_%7B1%7D%2Ca_%7B2%7D%2C...%2Ca_%7Br%7D)%7D$ , where $%7B%5Cdisplaystyle%20a_%7B1%7D%3Ca_%7B2%7D%3C%5Ccdots%20%3Ca_%7Br%7D%7D$ . The first choice is to be used on the first candidates starting with th Applicant, and once the first choice is used, second choice is to be used on the first candidate starting with th Applicant, and so on.

一个玩家可以有 r 个选择，如果任何一个选择是最好的，那么他就赢了。Gilbert & Mosteller 1966证明了一个最优策略是由一个阈值策略(截止策略)给出的。最优策略属于由一组阈值数字(a1，a2，... ，ar)定义的策略类，其中 a1 < a2 < ar。第一个选择用于第一个申请人，第一个选择用于第二个申请人，第二个选择用于第一个申请人，以此类推。

Gilbert and Mosteller showed that $%7B%5Cdisplaystyle%20%5Cleft(%7B%5Cfrac%20%7Ba_%7B1%7D%7D%7Bn%7D%7D%2C%7B%5Cfrac%20%7Ba_%7B2%7D%7D%7Bn%7D%7D%2C%7B%5Cfrac%20%7Ba_%7B3%7D%7D%7Bn%7D%7D%2C%7B%5Cfrac%20%7Ba_%7B4%7D%7D%7Bn%7D%7D%5Cright)%5Crightarrow%20%5Cleft(e%5E%7B-1%7D%2Ce%5E%7B-%7B%5Cfrac%20%7B3%7D%7B2%7D%7D%7D%2Ce%5E%7B-%7B%5Cfrac%20%7B47%7D%7B24%7D%7D%7D%2Ce%5E%7B-%7B%5Cfrac%20%7B2761%7D%7B1152%7D%7D%7D%5Cright)(n%5Crightarrow%20%5Cinfty%20)%7D$

. For further cases that r=5,6,...,10{\displaystyle r=5,6,...,10} , see Matsui & Ano 2016 (for example $%7B%5Cdisplaystyle%20%7B%5Cfrac%20%7Ba_%7B5%7D%7D%7Bn%7D%7D%5Crightarrow%20e%5E%7B-%7B%5Cfrac%20%7B4162637%7D%7B1474560%7D%7D%7D%7D$ ).

Gilbert 和 Mosteller 证明(a1n，a2n，a3n，a4n)→(e-1，e-32，e-4724，e-27611152)(n →∞)。关于 r = 5,6，... ，10的进一步情况，见 Matsui & Ano 2016(例如 a5n → e-41626371474560)。

When r=2{\displaystyle r=2} , the probability of win converges to $%7B%5Cdisplaystyle%20e%5E%7B-1%7D%2Be%5E%7B-%7B%5Cfrac%20%7B3%7D%7B2%7D%7D%7D(n%5Crightarrow%20%5Cinfty%20)%7D$ (Gilbert & Mosteller 1966).Matsui & Ano 2016 showed that for any positive integer r{\displaystyle r} , the probability of win (of r{\displaystyle r} choice secretary problem) converges to $%7B%5Cdisplaystyle%20p_%7B1%7D%2Bp_%7B2%7D%2B%5Ccdots%20%2Bp_%7Br%7D%7D$ where $%7B%5Cdisplaystyle%20p_%7Bi%7D%3D%5Clim%20_%7Bn%5Crightarrow%20%5Cinfty%20%7D%7B%5Cfrac%20%7Ba_%7Bi%7D%7D%7Bn%7D%7D%7D$ . Thus, the probability of win converges to $%7B%5Cdisplaystyle%20e%5E%7B-1%7D%2Be%5E%7B-%7B%5Cfrac%20%7B3%7D%7B2%7D%7D%7D%2Be%5E%7B-%7B%5Cfrac%20%7B47%7D%7B24%7D%7D%7D%7D$ and $%7B%5Cdisplaystyle%20e%5E%7B-1%7D%2Be%5E%7B-%7B%5Cfrac%20%7B3%7D%7B2%7D%7D%7D%2Be%5E%7B-%7B%5Cfrac%20%7B47%7D%7B24%7D%7D%7D%2Be%5E%7B-%7B%5Cfrac%20%7B2761%7D%7B1152%7D%7D%7D%7D$ when r=3,4{\displaystyle r=3,4} respectively.

当 r = 2时，获胜概率收敛到 e-1 + e-32(n →∞)(Gilbert & Mosteller 1966) 。Matsui & Ano 2016证明了对于任意正整数 r，r 选择秘书问题的胜算概率收敛于 p1 + p2 + something + pr，其中 pi = limn →∞。因此，当 r = 3,4时，胜利的概率分别收敛到 e-1 + e-32 + e-4724和 e-1 + e-32 + e-4724 + e-27611152。

Experimental studies

Experimental psychologists and economists have studied the decision behavior of actual people in secretary problem situations.[9] In large part, this work has shown that people tend to stop searching too soon. This may be explained, at least in part, by the cost of evaluating candidates. In real world settings, this might suggest that people do not search enough whenever they are faced with problems where the decision alternatives are encountered sequentially. For example, when trying to decide at which gas station along a highway to stop for gas, people might not search enough before stopping. If true, then they would tend to pay more for gas than if they had searched longer. The same may be true when people search online for airline tickets. Experimental research on problems such as the secretary problem is sometimes referred to as behavioral operations research.

实验心理学家和经济学家研究了实际人在秘书问题情境中的决策行为。[9]在很大程度上，这项研究表明，人们往往过早地停止搜索。这至少部分可以用评估候选人的成本来解释。在现实世界的环境中，这可能意味着当人们遇到决策选择依次出现的问题时，他们搜索的不够。例如，当试图决定在高速公路上的哪个加油站加油时，人们可能在停车前搜索不够。如果这是真的，那么他们将倾向于支付更多的天然气比如果他们搜索更长的时间。当人们在网上搜索机票时，情况可能也是如此。对秘书问题等问题的实验研究有时被称为行为操作研究。

Neural correlates

While there is a substantial body of neuroscience research on information integration, or the representation of belief, in perceptual decision-making tasks using both animal[10][11] and human subjects,[12] there is relatively little known about how the decision to stop gathering information is arrived at.

Researchers have studied the neural bases of solving the secretary problem in healthy volunteers using functional MRI.[13] A Markov decision process (MDP) was used to quantify the value of continuing to search versus committing to the current option. Decisions to take versus decline an option engaged parietal and dorsolateral prefrontal cortices, as well ventral striatum, anterior insula, and anterior cingulate. Therefore, brain regions previously implicated in evidence integration and reward representation encode threshold crossings that trigger decisions to commit to a choice.

History

The secretary problem was Apparently introduced in 1949 by Merrill M. Flood, who called it the fiancée problem in a lecture he gave that year. He referred to it several times during the 1950s, for example, in a conference talk at Purdue on 9 May 1958, and it eventually became widely known in the folklore although nothing was published at the time. In 1958 he sent a letter to Leonard Gillman, with copies to a dozen friends including Samuel Karlin and J. Robbins, outlining a proof of the optimum strategy, with an Appendix by R. Palermo who proved that all strategies are dominated by a strategy of the form "reject the first p unconditionally, then accept the next candidate who is better". (See Flood (1958).)

The first publication was Apparently by Martin Gardner in Scientific American, February 1960. He had heard about it from John H. Fox Jr., and L. Gerald Marnie, who had independently come up with an equivalent problem in 1958; they called it the "game of googol". Fox and Marnie did not know the optimum solution; Gardner asked for advice from Leo Moser, who (together with J. R. Pounder) provided a correct Analysis for publication in the magazine. Soon afterwards, several mathematicians wrote to Gardner to tell him about the equivalent problem they had heard via the grapevine, all of which can most likely be traced to Flood's original work.

The 1/e-law of best choice is due to F. Thomas Bruss (1984).

Ferguson (1989) has an extensive bibliography and points out that a similar (but different) problem had been considered by Arthur Cayley in 1875 and even by Johannes Kepler long before that.

Combinatorial generalization

The secretary problem can be generalized to the case where there are multiple different jobs. Again, there are n{\displaystyle n} Applicants coming in random order. When a candidate arrives, she reveals a set of nonnegative numbers. Each value specifies her qualification for one of the jobs. The administrator not only has to decide whether or not to take the Applicant but, if so, also has to assign her permanently to one of the jobs. The objective is to find an assignment where the sum of qualifications is as big as possible. This problem is identical to finding a maximum-weight matching in an edge-weighted bipartite graph where the n{\displaystyle n} nodes of one side arrive online in random order. Thus, it is a special case of the online bipartite matching problem.

By a generalization of the classic algorithm for the secretary problem, it is possible to obtain an assignment where the expected sum of qualifications is only a factor of e{\displaystyle e} less than an optimal (offline) assignment.[14]