材料力学应力状态强度理论
书接上文,上次我们介绍了应力应变状态的相关知识点,这一节我们对应力圆和强度理论展开学习,这节知识点很重要哟~

1.三向应力圆
如图所示,以三个主应力表示的单元体,由三个相互垂直的平面分别作应力圆,将三个平面的应力圆绘在同一平面上得到三向应力状态下的应力圆,如图所示。
与每一主应力所对应的应力圆可由与该主平面相正交的其余面上的应力作出。
注意:作三向应力圆应至少知道一个主应力的大小和方向。


2.应力圆方程
l、m、n 分别表示面 ABC 的法线 n 的三个方向余弦,可得
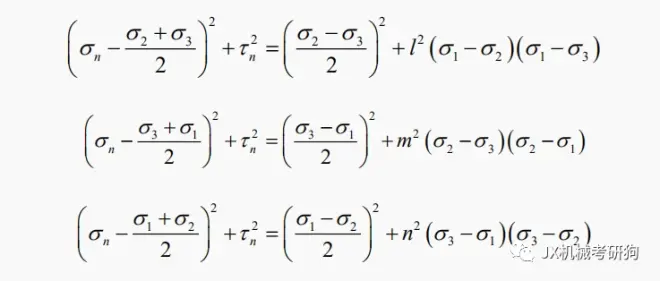
3.应力圆的应用
(1)确定任意斜截面上的应力
应力圆方程的第一式所确定的圆周在圆周 B1C1 之外,第二式所表示的圆周在圆周 A1B1 之内,第三式所表示的圆周在圆周 A1C1 之外。因而上述三个圆周的交点 D,亦即斜面 ABC 上的应力应在图 图中画阴影线的部分之内。
(2)应力极值
①正应力:如图所示,点 A1、B1 和 C1 的横坐标分别代表主应力 ζ1、ζ2 和 ζ3。
②切应力:如图 7-1-5 所示,点 G1 的纵坐标代表切应力的极值,最大切应力为
ηmax=(ζ1-ζ3)/2
③方位:最大切应力所在平面与 ζ2 主平面平行,与 ζ1、ζ3 主平面夹角互为 45°。

四、平面应变状态(选学内容,不做要求)
1.任一方向的应变

主应变方向与主应力方向相同,主应变 ε1、ε2、ε3 与主应力 ζ1、ζ2、ζ3 对应;与应力圆类似,存在应变圆,与应力圆有相同的特点,不同点是 γ 的坐标有系数 1/2。
2.主应变计算公式

3.主应变方向公式
tan2α0=-γxy/(εx-εy)
五、广义胡克定律
本节所列公式均仅在各向同性材料线弹性小变形条件下使用,各向异性材料的广义胡克定律公式应以矩阵形式表示。
1.胡克定律
单向拉伸或压缩时,在线弹性范围内应力与应变的关系为ζ=Eε 或 ε=ζ/E此外,轴向的变形将引起横向尺寸变化,横向应变可表示为
ε′=-με=-μζ/E
2.剪切胡克定律
在纯剪切的情况下,当切应力不超过剪切比例极限时,切应力和切应变之间的关系为
η=Gγ或 γ=η/G
3.广义胡克定律
以图所示坐标系下的单元体为例。
(1)x、y、z 方向的线应变
εx=[ζx-μ(ζy+ζz)]/E
εy=[ζy-μ(ζz+ζx)]/E
εz=[ζz-μ(ζy+ζx)]/E
(2)xy、yz、zx 三个面内的切应变
γxy=ηxy/G
γyz=ηyz/G
γzx=ηzx/G
(3)主应力-主应变的关系
ε1=[ζ1-μ(ζ2+ζ3)]/E
ε2=[ζ2-μ(ζ3+ζ1)]/E
ε3=[ζ3-μ(ζ1+ζ2)]/E
此时,三个坐标平面内的切应变等于零,主应变与主应力的方向重合。

4.体积胡克定律
(1)体应变:单位体积的体积改变量,用 θ 表示,其计算式为

(2)体积胡克定律:体应变计算公式可用体积弹性模量 K 和三个主应力的平均应力 ζ m来表示,
即θ=ζm/K。式中,K 为体积弹性模量,K=E/[3(1-2μ)];ζm为主应力平均值ζm=(ζ1+ζ2+ζ3)/3。
注意:单位体积的体积改变只与三个主应力之和有关。
六、复杂应力状态的应变能密度
物体在单位体积内所积蓄的应变能称为应变能密度。
1.应变能密度计算公式
(1)单向应力状态下,物体内所积蓄的应变能密度为
νε=ζε/2=ζ2/(2E)=Eε2/2
(2)三个主应力同时存在时,单元体的应变能密度为

(3)应变能密度的组成
应变能密度由体积改变能密度 νV和畸变能密度 νd 两部分组成,即νε=νV+νd
①体积改变能密度:单元体体积改变而储存的应变能密度,用 νV表示,计算式为

此时,单元体只发生体积变化,形状不变。
②畸变能密度:单元体形状改变而储存的应变能密度,用 νd 表示,计算式为
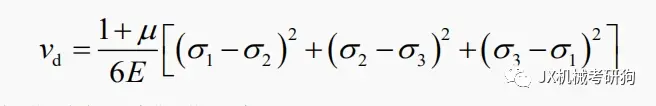
此时,单元体只发生形状变化,体积不变。
2.三个弹性常数间的关系
G=E/[2(1+μ)]
3.计算复杂应力状态的应变能注意事项
(1)应变能的大小只决定于外力和变形的最终数值,而与加力次序无关。
(2)应变能的计算不能采用叠加原理。
七、强度理论
材料失效形式主要有屈服失效和断裂失效两种。
(1)屈服失效:材料出现显著的塑性变形而丧失其正常的工作能力。
(2)断裂失效:有脆性断裂和韧性断裂两种形式。
其中,脆性断裂是指在无明显的变形下突然断裂;韧性断裂是指在产生大量塑性变形后断裂。1.常用强度理论
常用强度理论主要适用于常温静载荷下的均匀、连续、各项同性材料。
(1)第一强度理论(最大拉应力理论)
①理论假定:最大拉应力是引起断裂的主要因素;
②断裂准则:ζ1=ζb;
③相当应力:ζr1=ζ1;
④强度条件:ζr1≤[ζ]。
(2)第二强度理论(最大伸长线应变理论)
①理论假定:最大伸长线应变是引起断裂的主要因素;
②断裂准则:ζ1-μ(ζ2+ζ3)=ζb;
③相当应力:ζr2=ζ1-μ(ζ2+ζ3);
④强度条件:ζr2≤[ζ]。
(3)第三强度理论(最大切应力理论)
①理论假定:最大切应力是引起屈服的主要因素;
②屈服准则:ζ1-ζ3=ζs;
③相当应力:ζr3=ζ1-ζ3;
④强度条件:ζr3≤[ζ]。
(4)第四强度理论(畸变能密度理论)
①理论假定:畸变能密度是引起屈服的主要因素;
②屈服准则

③相当应力:

④强度条件:ζr4≤[ζ]。
(5)常用强度理论的选取

2.莫尔强度理论
(1)相当应力:ζrM=ζ1-[ζt]ζ3/[ζc]。
(2)强度条件:ζrM≤[ζt]。
(3)莫尔强度理论与常用强度理论的对比:
由莫尔理论可以得出第三强度理论的强度条件,往往把它看作是第三强度理论的推广。
但有本质区别:莫尔理论是以实验资料为基础,经合乎逻辑的综合得出的,并非以失效假说为基础。因此,莫尔理论的方法是比较正确的。
3.构件含裂纹时的断裂准则
假设与裂纹的尺寸相比,平板的长与宽可认为是无限大的,材料是线弹性的。
①应力强度因子穿透平板厚度的裂纹长为 2a,裂纹尖端附近各点的应力,成比例地增长或减少, πa称为应力强度因子,并记为 KI。
②断裂准则:KI=KIc,式中,KIc为断裂韧性,是材料的固有力学性能。

https://mp.weixin.qq.com/s?__biz=MzIyNjE0NDA5Mg==&mid=2247484339&idx=1&sn=9590416b8e5acaa7f61ceda424905cb3&chksm=e875b980df023096993c57cc7762c6a1efcca32458246512ef9e92186874bcb3949f39bf6332&scene=178&cur_album_id=2528330897279696899#rd

