语法分析程序的设计与实现-编译原理
项目4 使用递归下降法手动构建语法分析器
一、目的与要求
1)目的
通过设计、编制、调试一个确定的自顶向下语法分析程序,实现对词法分析程序所提供的单词序列进行语法检查和结构分析,并建立相应的语法树,进一步掌握常用的语法分析方法。
2)要求
用递归下降法分析、设计和实现TINY语言源程序的语法分析程序。
输入:单词序列
输出:语法树(语法正确),有语法错误,则报错
二、语法分析说明
TINY语言的文法:

中文描述:

文法的定义可以看出,TINNY语言有以下特点:
1) 程序共有5种语句:if语句,repeat语句,read语句,write语句和assign语句。
2) if语句以end作为结束符号,if语句和repeat语句允许语句序列作为主体。
3) 输入/输出由保留字read和write开始。read语句一次只读出一个变量,而write语句一次只写出一个表达式。
三、语法树的设计
1) TINY有两种基本的结构类型:语句和表达式。语句共有5类:(if语句、repeat语句、assign语句、read语句和write语句),表达式共有3类(算符表达式、常量表达式和标识符表达式)。因此,语法树节点首先安装它是语句还是表达式来进行分类,接着根据语句或表达式的种类进行再次分类。
2) 树节点最大可有3个孩子的结构(仅在带有else部分的if 语句才用到)。同一级的语句通过同属域而不是子域来排序,孩子则在一个标准连接表中自左向右连接到一起,这种连接称作同属连接,用于区别父子连接。
(1)if 语句(带有3个可能的孩子)如下所示:

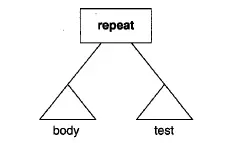
(2)repeat 语句有两个孩子。第1个是表示循环体的语句序列,第2个是一个测试表达式:

(3) assign 语句有一个表示其值是被赋予的表达式的孩子(被赋予的变量名保存在语句节点中):

(4) write 语句也有一个孩子,它表示要写出值的表达式:

(5)Read语句,没有孩子

(6)表达式有两个孩子,它们表示左操作数表达式和右操作数表达式:

3) 一个Tiny语法树节点的C声明如下:
typedef enum {StmtK,ExpK} NodeKind;
typedef enum {IfK,RepeatK,AssignK,ReadK,WriteK} StmtKind;
/* ExpType is used for type checking */
typedef enum {Void,Integer,Boolean} ExpType;
#define MAXCHILDREN 3
typedef struct treeNode{
struct treeNode * child[MAXCHILDREN];
struct treeNode * sibling;
int lineno;
NodeKind nodekind;
union { StmtKind stmt; ExpKind exp;} kind;
union {
TokenType op;
int val;
char * name; } attr;
} TreeNode;
4) 下面画出语法树的结构,用矩形框表示语句节点,用圆形框或椭圆形框表示表达式节点。仍然以Tiny语言的阶乘为例,给出Tiny程序的语法树。
程序清单1是该语言的一个求阶乘的编程示例。
程序清单1
{ Sample program
in TINY language -
computes factorial
}
read x; { input an integer }
if 0 < x then { don't compute if x <= 0 }
fact := 1;
repeat
fact := fact * x;
x := x - 1
until x = 0;
write fact { output factorial of x }
end

四、 用递归下降法进行语法分析程序的设计实现
递归下降法的实现思想就是对应文法中的每个非终结符,编写一个递归过程,每个过程的功能是识别该非终结符推出的串。当某个非终结符的产生式有多个候选时能够按照LL(1)的形式唯一地确定选择某个候选进行推导。
构造递归下降分析程序时,每个函数名是相应的非终结符,函数体根据产生式规则右部符号串的结构编写,基本思路如下:
(1) 当遇到终结符a时,则编写语句:
If (当前读来的输入符号==‘a’)读入下一个输入符号
(2) 当遇到非终结符A时,则编写语句调用A()
(3) 当遇到A®e产生式规则时,则编写语句:
If(当读来的输入符号不属于Follow(A))error()
(4) 当某个非终结符有多个候选产生式规则时,则:
if(当前读来的输入符号属于Select(ai))则按规则A®ai进行推导
1)对于产生式
< STMT-SEQUENCE > ::= <STMT-SEQUENCE> ; <STATEMENT>
| <STATEMENT>
产生的句型应该是: < STATEMENT > ; <STATEMENT> ; <STATEMENT> …..
产生的树结点:

我们可以构造出对应的程序:
TreeNode* stmt_sequence(void)
{
TreeNode* t = statement();
TreeNode* p=t;
while(token==SEMI)
{
match(SEMI);
TreeNode* t1=statement();
p->sibling = t1;
p=t1;
}
return t;
}
(2) STATEMENT := <IF-STMT> | <REPEAT-STMT>
| <ASSIGN-STMT> | <READ-STMT>
| <WRITE-STMT>
static TreeNode* statement()
{
TreeNode * t = NULL;
switch (token)
{
case IF: t = if_stmt(); break;
case REPEAT: t = repeat_stmt(); break;
case ID: t = assign_stmt(); break;
case READ: t = read_stmt(); break;
case WRITE: t = write_stmt(); break;
default:
{
char t[100];
sprintf(t, "unexpected token: %s", tokenString);
syntaxError(t);
}
}
return t;
}
< REPEAT-STMT > ::= repeat <STMT-SEQUENCE> until <EXP>
< SIMPLE-EXP> ::= <SIMPLE-EXP> + - <TERM>
| <TERM>
产生的句型:<TERM> + | - <TERM> + | -<TERM>

表达式:a+b-c+30
五、出错处理
错误处理的任务:(1)报错,发现错误时应尽可能准确指出错误位置和错误属性(2)错误恢复,尽可能进行校正,使编译工作可以继续下去,提高程序调试的效率。为了简单,本语法分析程序的出错处理为报告出错的行数,程序退出。
本实验采用的出错处理简单的处理为:一旦发生错误,就报错后编译停止
四、实验内容
(1)读懂源代码,添加注释,补充空白处的代码
(2)测试求阶乘的编程示例s.tiny ,输出语法树
{ Sample program
in TINY language -
computes factorial
}
read x; { input an integer }
if 0 < x then { don't compute if x <= 0 }
fact := 1;
repeat
fact := fact * x;
x := x - 1
until x = 0;
write fact { output factorial of x }
end
(3)测试编译gcd.tiny ,如果有语法错误,请修改语法后,输出语法树
{
求最大公约数
}
read m; { input an integer }
read n;
if m<n then { 将大数放入m中,小数放入n中}
t:=m;
m:=n;
n:=t;
end
repeat
q:=m/n;
r=m-q*n;
m:=n;
n:=r;
填充代码1:
TreeNode* if_stmt()
{
// 【代码1】 填充此代码
TreeNode *t = newStmtNode(IfK);
match(IF);
t->child[0] = exp_stmt();
match(THEN);
t->child[1] = stmt_sequence();
if(token==END)
{
match(END);
return t;
}
if(token==ELSE)
{
match(ELSE);
t->child[2] = stmt_sequence();
match(END);
return t;
}
return NULL;
}
TreeNode* read_stmt()
{
// 【代码2】 填充此代码
TreeNode *t = newStmtNode( ReadK);
match(READ);
char* idname= copyString(tokenString);
match(ID);
t->attr.name=idname;
return t;
}
static TreeNode* term()
{
// 【代码3】 填充此代码
TreeNode *t = factor();
while(token==TIMES||token==OVER)
{
TreeNode *p = newExpNode(OpK);
p->child[0] = t;
p->attr.op = token;
match(token);
TreeNode *q = factor();
p->child[1] = q;
t=p;
}
return t;
}
运行结果
Test1:

Test2:


