我们可以从之前的示例里看到，它们的推导过程很清晰，但总感觉少了一点什么。下面我们来看看这些引起我们思考的地方。

Part 1 同宫定理

第一个我们要介绍的内容就是同宫定理。同宫定理是一种神奇的定理，但使用范围有限。我们先来看看它到底是怎么用的。

如图所示，这个结构是一个标准的JE，我们已经不用再去叙述逻辑了，删数就是这里浅红色r2c4(26)和r3c7(9)。现在我们尝试来看看它还能得到什么结论。

我们尝试观察b5689里的所有1、5、8的确定值的分布。我们发现1和8是同宫的，而5是单独处于b6和b8的。同宫定理是：假设基准单元格里涉及的数字是a、b、c三种不同的数字，那么去尝试找交叉线单元格所属的六个宫里，和两个基准单元格不同行列的剩下四个宫里，a、b、c的确定值的分布。如果其中两种数字处于同宫的分布，那么基准单元格里就一定是这一组数字，即，基准单元格就是这两个数字构成的数对形式。

这句话有些绕，我们一步一步分析。首先，1、5、8就是这个定理说到的a、b、c三种数字，然后观察交叉线单元格分属的六个宫b456789，然后发现，基准单元格所在行列包含b47，所以剩下我们要观察的四个宫是b5689。然后发现1、5、8的确定值里，1和8是同宫的，所以基准单元格就是关于1和8的数对。于是，删除掉r1c12(5)。

这个定理非常好用，但具有一定的局限性。目前从定理来看，首先基准单元格必须是两个，而且必须涉及的是三种不同数字，如果是四个甚至更多，是都不行的。而且就目前来看，我们无法给出这个定理的证明。而且，使用上也有局限性。

如图所示，我们发现5和7同宫（b8），但这个示例依旧不能直接使用。我们所认为的同宫，必须是对角分布都需要存在同宫的要求。比如这一则示例里，b8是同宫的，但与之对角的b6却不是5和7同宫的；而b6却只有5没有7。所以这一个示例无法使用同宫定理得到结论。

对比之前的示例，1和8是同宫的，而处于对角的两个宫b5和b9都是同宫的，所以它才满足了同宫定理的要求。

所以，这一点很重要。

至于这个定理的论证，我们不会在这里提到，因为它的思路比较复杂。我们还有一个定理，它的逻辑和论证将在后面给出，而且它恰好包含了同宫定理的内容。

Part 2 T数对定理

第一个最容易想到的推论，就是目标单元格的跨区数对了。由于最后两处的填数是不同的，所以两个单元格只能一个a一个b，它们便形成了关于a和b的跨区数对，只是删数我们还不知道，因为a和b是未知数。如果我们后续的推导里可以得到a和b究竟是什么的时候，我们就可以顺理成章地得到跨区数对的删数了。

因为同宫定理目前不能使用在涉及四种数字的情况下，所以我们也无法使用同宫定理来进行删数。但是，如果只有三种数，那么就可以得到结论了：

如图所示，我们可以利用同宫定理得到的是，基准单元格里是2和9，那么根据JE的理论，我们还可以得到的是目标单元格里也是2和9，因为基准单元格是a和b，那么目标单元格里也是a和b，而且填数还不一样。

那么，由于是2和9的跨区数对的关系，r1c46和r3c89就显然不能放其它的2和9了，删掉它们。

这个定理跟目标单元格有关，而目标单元格target的首字母是T，所以称为T数对（Target Pair）。

我们再来看一则比较难理解的例子。

如图所示，我们可以根据基本的JE的删数形式得到目标单元格的删数。不过还不够，此时我们着重去看伴单元格r4c1和r6c4的镜面单元格r4c23和r6c56。

我们发现，r5仅剩下四个单元格。我们小范围使用代数法，假设r5c89是a和b，那么1、2、3、8的剩下两个数假设为c和d，此时只能放在r5c14里，我们可以随意假设c和d的位置，反正都是一样的。

a和b也是一样，目标单元格有两个，随便哪一个是a都行，这并不影响后续的推导。那么此时，我们可以得到上图这样的填数模式。显然，我们必然得到了r4c4是b，而r5c1是c，r6c1是a，而发现r4c23里只有1、2、3、8和额外的数字9。因为a、b、c都出现了，那么这两个单元格里只能放下一个d和一个9，否则的话，两个单元格只剩下1、2、3、8，而其中三种数都不能放入r4c23里，所以必须让9放进去，故r4c23里存在一个9区块；同理，下面的r6c56也应当通过类似的结论得到含有5区块的结论。

显然，由于5区块和9区块的成立，图中对应的区域里自然就可以删除掉这些数字，这里就不画出来了。

Part 3 T邻/镜面单元格定理

和目标单元格有关的还有一个定理，我们称为T邻定理，或镜面单元格定理，因为它跟镜面单元格有关。

3-1 原理

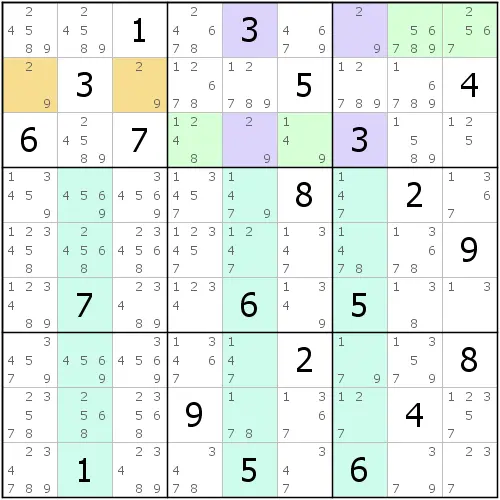
如图所示，我们通过之前的定理可以确定的删数，能做到这里。不过，我这次把镜面单元格也涂上了颜色，这意味着镜面单元格也有结论，不过是什么结论呢？

我们知道基准单元格一定是2和9了，那么r1c7和r3c5就一定是2和9，不过究竟哪一个单元格是2，哪一个是9我们目前还不知道。不过请思考一下。假如r1c7填入的是2，那么r3c5就是9，那么会如何呢？

如果r1c7是2，而r2c13里必有一个2，这就使得了r3c5的两个镜面单元格r3c46必须有一个是填2的，因为2在b2里只剩下这两个单元格可以填入2了；同理，由于r3c5是9，所以b3里此时能放9的位置只有r1c89，所以r1c7的镜面单元格r1c89里必须有一个9。

这就是T邻定理的内容：如果我们确定了基准单元格一定是填入a和b的，而某一个目标单元格填入了数字a，那么它自己的镜面单元格就必须有一个单元格是填入b的；或者把a和b换过来也可以。

那么，这个定理能不能反过来用呢？当然可以。根据逆否命题，如果镜面单元格里不包含我们需要的数字a和b的话（取原命题的反面情况），那么对应的目标单元格里就不能说明填入的数字一定是a和b，此时的JE就不一定成立了。因为原命题和逆否命题等价，所以这样理解是完全可以的。

这个内容有什么用处呢？我们来看一些示例。

3-2 示例1：带死锁区块的JE

如图所示。仔细观察这个结构，它有点不像是之前熟悉的JE结构，因为基准单元格里含有的数字9在交叉线单元格里有确定值的出现。我们之前的推导逻辑里，基准单元格里涉及的所有数字在交叉线单元格里都没有确定值的出现的。

显然，这个结构的数字9出现了这样的情况，我们就无法当作JE来使用，不过我们可以换一种思考方式：正难则反。假设基准单元格r4c23里不含有候选数9的话，那么JE就明显是成立的了，因为1、2、3、8四种数字在交叉线单元格里最多都只能出现两个，所以在c147的剩余部分r456c147里，1、2、3、8都最少需要出现一次。假设r4c23填入的是a和b（此时a和b是1、2、3、8的其二，且不相同），那么我们可以顺理成章地得到目标单元格r5c4和r6c7里都只能是a和b。而1、2、3、8显然就是这里a和b的候选情况，所以自然就删掉和1、2、3、8无关的数字。

不过可以从图上看出，r6c7似乎把1、2、3、8这些需要的数字全删掉了，说明上述推导有错。那么错误在哪里呢？错误在于，我们说过，如果JE成立，那么就可以尝试使用T邻定理来得到镜面单元格的结论。显然，如果r5c4填入a，而r6c7填入b的话，那么r5c4的镜面单元格r5c56里就必须有一个是数字b（且b一定是1、2、3、8的其一）。不过可以从图上看出，r5c56都是确定值，且是6和9，跟1、2、3、8全部无关。这就说明了矛盾的出现：原本我们要求JE成立后，一定会得到镜面单元格必须是1、2、3、8的其一，结果却出现的是6和9，这显然不对，所以原假设错误，即r4c23里必须有一个9，即形成了9区块。

那为什么删除的数字是r6c7(1238)呢？显然，我们可以通过9的确定值看出，b6此时能放9的位置只有r6c7，所以r6c7 = 9。

类似于这种使用的，还有一些示例。

3-3 示例2：另一则带死锁区块的JE

如图所示。我们尝试假设r1c46没有候选数6，那么交叉线单元格就不需要看6的相关填数位置，此时1、3、4、8都最多出现两次，所以r123c158里至少出现一次1、3、4、8。而假设r1c46填入a和b（此时a和b是1、3、4、8的其二，且不相同），那么最终a和b只能放在r2c1和r3c8里。

不过根据T邻定理，我们可以看到r2c1的镜面单元格含有5和6的确定值，但它们跟1、3、4、8无关，所以出现矛盾。所以，原本假设错误，即r1c46(6)区块是成立的，故我们可以利用这个区块，得到r3c8 = 6的结论。

3-4 示例3：只有T邻定理删数的JE

如图所示，我们可以通过基本的推理逻辑得到目标单元格r7c4和r8c9填入的是2、6、8、9的其二，不过此时依然没有删数。不过我们不能气馁，因为这个例子隐藏了一个巨大的T邻定理的使用方法。

可以发现，假如我们设r9c13填入a和b，且r7c4是a、r8c9是b的话，那么根据T邻定理可以得到，r8c8一定是a，而r7c56里有一个是b。那么，r8c8为啥一定是a呢？因为r8c9的镜面单元格r8c78里必须有一个a，这是T邻定理规定的结论；而其中的r8c7是4的确定值，而它并不在2、6、8、9其中，所以能放a的地方就只剩下r8c8了。

所以，r8c8是a。换而言之，r8c8不应当是2、6、8、9外的数字，删掉它们。此时又可以发现，r8c8填入的是a，根据代数法的原理，原本假设为a的地方，就必须是填入a的，所以目标单元格r7c4就一定也是这些候选数。r8c8只有2和9，那么r7c4也只能有2和9，删除掉6和8。

3-5 示例4：需要T邻定理删数的第二类JE

如图所示，它的逻辑和前面这一则示例推导逻辑完全一样，不过用到的是第二类JE的论证出现至少两次的逻辑。推导只有这一点不同，所以这里就不再给出示例的说明了，请你自己分析。

需要注意的是，删数一定要是同步的。比如T邻定理得到的候选数是怎么样的，可以根据代数法代入回原本的目标单元格，得到候选数一致的结论，这一点别漏掉了。

3-6 示例5：同时有共轭对和死锁区块的JE

如图所示，首先我们可以通过JE直接得到目标单元格内的删数。接着我们可以观察r3c7的镜面单元格r3c89有什么结论。

我们按照期望先假设r23c7填入的是b和7（7是共轭对导致的），而r2c4假设填入的是a。那么r23c7究竟哪一个是7，哪一个是b，我们不清楚，所以分两种情况来分析。

假如r2c7 = b，那么此时形成的目标单元格就位于同一侧了，而此时r1c12这一对基准单元格填入的肯定是a和b，所以我们把a提出来，针对于b3作出排除，可以发现a只能放到r3c89里，而b3（或者说r3）上存在5的共轭对，这意味着r3c89里必须有一个是a，另外一个是5。而r3c89填入的数字跟a（1、2、3其一）和5以外的数字无关，所以可以删除掉它们；

假设r3c7 = b，那么此时更容易地确定到a的填数位置在r3c89，因为这里可以直接利用T邻定理得到结论。所以照样r3c89是a和5，跟其余的候选数无关，删除掉它们。

Part 4 三链列/剑鱼定理

当然，还是前面这个示例那道题。除了我们可以删除这些以外，还有一些删数，是通过三链列得到的，所以这个定理称为剑鱼定理或者三链列定理（Swordfish Theorem）。这个理论的名称是我自己本人给出的。

如图所示，图上给出了关于2和9的三链列结构。注意，r1c7(2)和r3c5(2)是可以通过弱关系连起来的，同理，r1c7(9)和r3c5(9)也是一样。为什么呢？因为它们不同真，同真就违背了JE的原则——目标单元格的填数是不同的。那么，形成剑鱼后，我们就可以通过2和9找到各自额外的删除域的删数，至于r1c7和r3c5弱关系连起来的对应区域，我们已经通过跨区数对删除了，就是跨区数对可以删掉的那些2和9。所以这个定理能够删除的数字如下。

显然，这个定理依旧需要先得到跨区数对的结论。

Part 5 X致命定理

下面来说一个得到比较困难的定理：X致命定理（Bi-Bi Pattern）。这个定理将同宫定理进行了推广，但证明逻辑就会麻烦一些。

这个定理的英文名里的Bi是数字2的含义的前缀，读作[baɪ]。该理论由发明区分度理论、提出淑芬致命结构和宇宙法的中国数独玩家邱言哲和探长两人提出以及说明基本猜想，并由探长验证逻辑的正确性和严谨性，稍后将给出理论的证明。

5-1 使用

如图所示，我们只看JE的构型，可以通过基本的推导思路得到r7c9 <> 3的结论。因为这里我们着重解释该定理，所以我们就暂时不管这个删数，去看基准单元格到底有什么删数。

下面我们为了方便描述和表达，我们给出X区域的定义：

X区域（X-Region/Dual Region）：交叉线单元格里，以确定值为轴心，与交叉格分部方向正交的单元格排开，并排开基准格和交叉格能够直接对应的两个宫外的剩下四个宫的格子外，剩下的16格。例如图示里，所有浅红色（含深绿色和深青色）的16格为一个X区域。

该定理如下：X区域里，如果某两种数字的提示数能出现在对角的两个宫里，那么这两个数就一定不能组合产生于基准格里。举个例子，数字7出现于对角两个宫，而另外一个对角宫里2和4都是对角出现的，则就使得如果7出现到组合里，那另外一格填数必须不能是2或4，否则2、7和4、7组合均满足推论的要求，这就会使得基准单元格一定不允许为2、7和4、7组合。

接着因为基准格r12c7里有一个单元格含有候选数1，而另外一格又没有这个数字。如果这一个单元格填入7，则另外一格由于没有1的关系，只剩下2和4的填数情况，这必然形成了2和7以及4和7的组合。所以这必然是不允许的。所以假设错误，故r1c7不能填入7。

这个定理用起来非常神奇，而且非常匪夷所思，它把确定值和候选数层面直接关联起来了，而且也有固定的删数模式和原理。下面我们来看看这个定理如何证明。

5-2 证明

如图所示，我们构造出简图。为了满足题目所证明的需求，我们就构造出X致命原则的主要形成条件：a和b各自得在对角宫出现，并且不是相同的对角两宫；基准格就假设为a、b、c和d即可（假设a、b、c也是类似的证明）。

现有如图的推理情况的其一。我们继续向下推导。由于r4c8只能填a和b了，所以该行里r4c12和r4c45里，a和b的填数位置显然不可同真（即r4c12(b)和r4c45(a)形成弱关系）。注意，a和b的提示数此时已经在X区域里表示到图上了，所以图中的a和b的位置显然分别只能填入到r4c45和r4c12里面了。

同样地，下面的r7c12和r7c45也有此类似的关系。此时我们使用链表示出来：

此时继续观察该图。由于下面r89c45里有一个a，而上面r4c45里也能有a，那请问r34c45四格里a的位置能有几个呢？是不是只有一个了！交叉格里只能有最多两个a，上面r4c45里如有a，那上面的r3c45就不能有a，不然r34c45都有a的话，就一定会有一个a和下面r89c45里的a的提示数重复，违背要求。因此r4c45(a)和r3c45(a)不可同为真；另外一方面，能不能同为假呢？如果同为假的话，那a要保证恰好两个的地方只有r3c12和r7c12了。之所以此处说恰好两个而不是至少两个的原因很简单：结论一个a和一个b的结果已经得到，这使得此时填入a的位置在交叉格里必须得是两个，毕竟r4c8和r7c9里已经有一个a了。

那既然r37c12里有a的话，那可不可能填两个呢？显然不能。因为r37c12同时都可以“对应到”r56c12的a的提示数上，如果r37c12同为a，显然会有一个a会和a的提示数矛盾。这下，r3c45(a)和r4c45(a)更不能同为假。既然不能同为真，也不能同为假，那么r3c45(a)和r4c45(a)只能是一个真和一个假（即它同时满足强关系也同时满足弱关系）。

继续。我们此处为了能够继续推理，我们使用r3c45(a)和r4c45(a)的强关系，为了能把链串起来。刚才的结论只能得到这么一点结论吗？显然不是，我们来看看真正能连上的位置：

所有强弱关系的证明方式，都可以从刚才的证明逻辑之中得到，这里就不一一证明了。

试想一下。这样构成了两条链，一条是“内线”，一条是“外线”。b假得a真，a假又得b真，又恰好涉及的是同样的两个部分r3c12和r3c45，那么这就只可能说明一点：a和b是挨着的，而不是让r3c12和r3c45一边一个。既然a和b是挨着的，我们就可以粗略地叙述为“a和b在此处的填数是同宫的”。如果同宫，则就表示这里形成了显然的a和b的数对。那么形成数对又会怎么样呢？

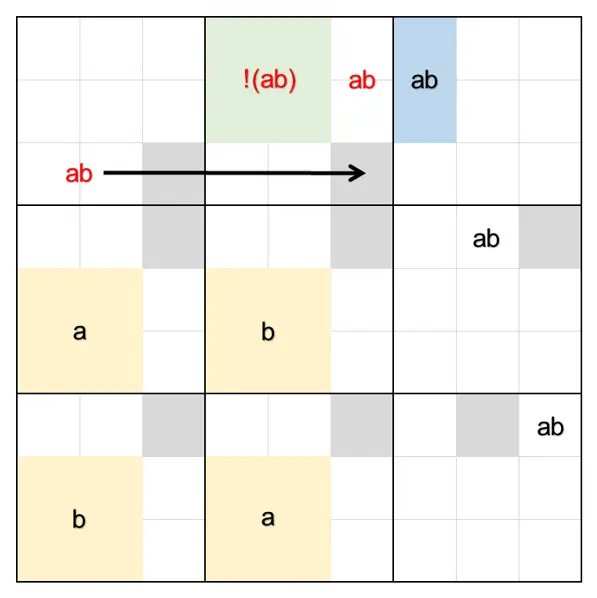
如图所示，假设我们的a和b的数对在第一个宫挨着的地方，根据排除效果，显然r3c6就不能是a和b了；而根据刚才的原理，r12c45此时是不可以为a和b的。那此时a和b就只可以填到r12c6里。至此r12c6形成a和b的数对。

此时再结合上r12c7的a和b，此时r12c67形成关于a和b的唯一矩形的致命形式，所以矛盾了。证毕。

如果你把这个证明逻辑套用到三个数的JE结构，同宫定理是适用的，原理可通过X致命定理的原理直接证明得到。

1、3、6里，1和3的组合，以及1和6的组合是不可以同时出现的，否则形成上述的致命形式（当然也可能中途就没办法填数导致死亡了），所以三个数的组合只剩下3和6是可以的，而正是因为组合只能是3和6的关系，这就看起来好像3和6恰好同宫，就可以用了，所以这便通过X致命定理简单地证明了同宫定理。

下面我们来看一些例子。

5-3 一些使用示例

如图所示，我们发现，5和6是不能形成组合放到r1c12里的，因为b5689里5和6的确定值的分布构成了X形状，这样就保证了X致命定理的出现。所以r1c12不能是5和6的数对。

那么，r1c2 <> 56就很好理解了。假设r1c2 = 5，则r1c1只能放入5或者6，使其形成5、6数对，必然出错；r1c6 = 6时也是一样。所以r1c12 <> 56。

如图所示。r5c8(7)删数的原理就不再赘述了。我们发现，b1379里，9和1、8组合都会形成X致命形式，所以基准单元格r6c56里不能是1、9数对和8、9数对。

如果r6c6 = 9，那么r6c5此时只能放入1或8，而这都是不行的，所以r6c6 <> 9的结论就直接通过这个定理得到了。

Part 6 小练习

那么，基本的一些定理就说完了，下面来看一个示例，可以通过基本的定理删除掉这些候选数。请自行理解，并尝试找到每一个删数的真正删数原因。