郑涛（Tao Steven Zheng）著

【问题】

宋元时期（公元 960年 - 1368年）的数学家研究了与贾宪三角对角线有关的有限级数（finite seies）。以下列表给出了朱世杰《算学启蒙》（1299）和《四元玉鉴》（1303）中的级数。

茭草垛

落一形垛

撒星形垛

撒星更落一形垛


这些有限级数叫高阶等差级数（arithmetic series of higher order），遵循一般公式

也可以写成

证明这个恒等式。

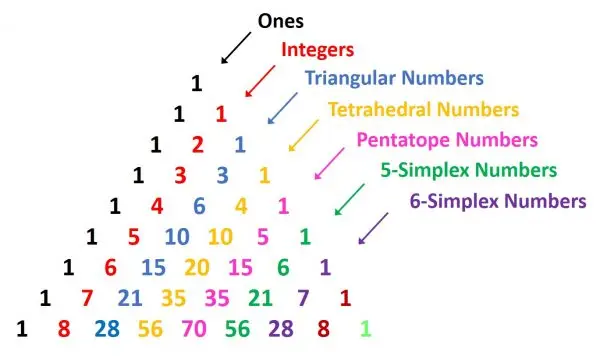
【题解】

注意 ，所以

使用二项式恒等式 ，得

遵循这个步骤模式

直到最后两项

因此，