【今日数学】圆环面 Torus
郑涛(Tao Steven Zheng)著
【什么是圆环面?】
圆环面(torus)是一个圆绕平面上与圆不相交的一个轴旋转而形成的旋转曲面(surface of revolution)。如果旋转轴(axis of revolution)不接触圆,该曲面称为环形环面(ring torus)。如果旋转轴与圆相切,该曲面称为角环面(horn torus)。如果旋转轴两次穿过该圆,该曲面称为纺锤环面(spindle torus)。
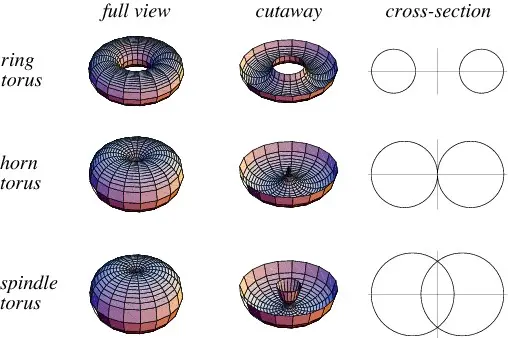
【What is a torus?】
A torus is a surface of revolution generated by revolving a circle about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface is called a ring torus. If the axis of revolution is tangent to the circle, the surface is called a horn torus. If the axis of revolution passes twice through the circle, the surface is called a spindle torus.
【圆环面的几何学】
设 为洞的中心到圆环面“管”的中心的距离,
为圆环面“管”的半径。那么,直角坐标系中的关于z-轴方位角对称的方程是
参数方程(parametric equations)为
其中 。
从这里可以推断, 对应于环形环面(ring torus),
对应于角环面(horn torus),
对应于纺锤环面(spindle torus)。
表面积
圆环面的表面积 是通过使用半径为
的圆之周长围绕穿过圆心的圆路径而形成的。其圆路径的半径为
。
体积
圆环面的内部体积 是通过使用半径为
的圆之面积围绕穿过圆心的圆路径而形成的。其圆路径的半径为
。
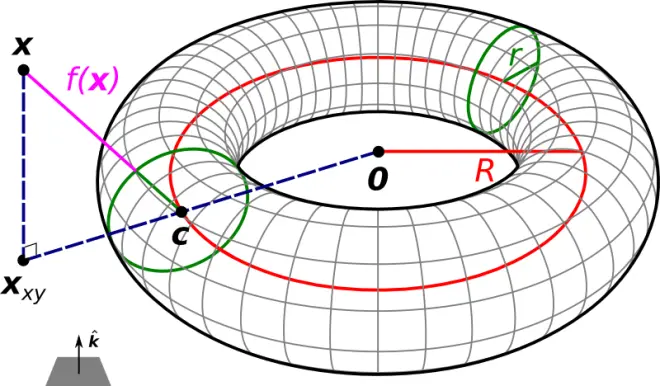
【Geometry of the Torus】
Let the distance from the center of the hole to the center of the torus "tube" be , and the radius of the torus "tube" be
. Then the equation
in Cartesian coordinates for a torus that is symmetric about the z-axis is
and the parametric equations are
where .
One can infer from here that corresponds to the ring torus,
corresponds to the horn torus, and
corresponds to the spindle torus.
Surface Area
The surface area of the torus is generated by rotating the circumference of the circle with radius
around a circular path that passes through the circle's center. The length of the path is the circumference of the circle with radius
.
Volume
The volume inside the torus is generated by rotating the area of the circle with radius
around a circular path that passes through the circle's center. The length of the path is the circumference of the circle with radius
.
【有趣的知识】
实心的圆环面是甜甜圈的形状,一种标志性的美国小吃。油炸面团通常中心会煮不熟透、外层又过熟。这是因为面团的中心没有外面快熟。1847年,美国船长汉森·格雷戈里(Hanson Gregory)解决了这个问题。他在油炸前在面团的中心打了一个洞。这个洞增加了面团的表面积,使面团的外部更多地接触到热油。所以,圆环面形的甜甜圈使面团煮得更均匀。

【Fun Fact】
The solid torus is the shape of the doughnut (more commonly spelled donut today), an iconic and popular American snack. An undercooked center and overcooked shell can often result when deep-frying dough cakes. This is because the center of the cake does not cook as fast as the outside. In 1847, Hanson Gregory (an American ship captain) resolved this problem by punching a hole in the center of dough cakes before frying. The hole increases the surface area, exposing more of the dough's exterior to the hot oil. In consequence, the torus-shaped donut makes the dough cook more evenly.

