Project Euler 084~087

关于啥是Project Euler 详见 https://projecteuler.net/about
观前声明:
这是个人兴趣使然的对自己入坑pe的记录,仅提供思路和部分代码; 各个方面肯定都是有着优化与提升空间的,甚至在许多大佬看来这应该是初学者的浅薄而未经剪枝的丑码,如果能帮到有兴趣的人自是最好,也欢迎能醍醐灌顶的深度讨论。
大佬看到了笑笑就行,还请轻喷。
带着恶意,抬杠者...俺也喷不过您,也不能拿您咋样...毕竟这只是我个人兴趣使然的行为或者说是学习记录分享。 (说是记录,但因为是早先写的所以其实是在各种意义上公开处刑和吐槽自己 并尝试补救优化)
语言是c++,用的VS平台
前排:本期莫得感情的暴搜机器.

Monopoly odds
Problem 84
In the game, Monopoly, the standard board is set up in the following way:
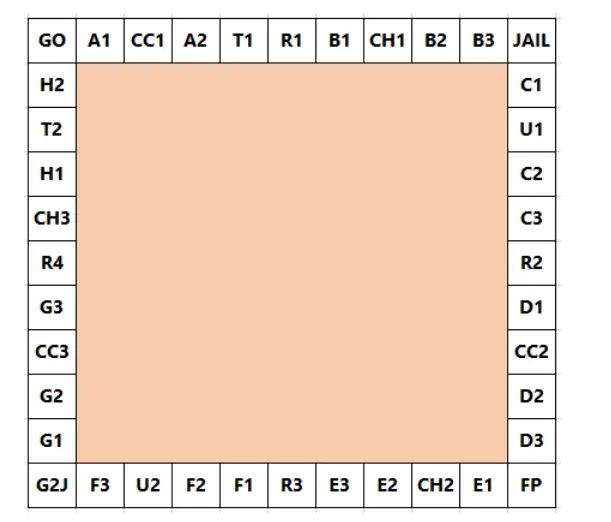
A player starts on the GO Square and adds the scores on two 6-sided dice to determine the number of Squares they advance in a clockwise direction. Without any further rules we would expect to visit each Square with equal probability: 2.5%. However, landing on G2J (Go To Jail), CC (community chest), and CH (chance) changes this distribution.
In addition to G2J, and one card from each of CC and CH, that orders the player to go directly to jail, if a player rolls three consecutive doubles, they do not advance the result of their 3rd roll. Instead they proceed directly to jail.
At the beginning of the game, the CC and CH cards are shuffled. When a player lands on CC or CH they take a card from the top of the respective pile and, after following the instructions, it is returned to the bottom of the pile. There are sixteen cards in each pile, but for the purpose of this problem we are only concerned with cards that order a movement; any instruction not concerned with movement will be ignored and the player will remain on the CC/CH Square.
Community Chest (2/16 cards):
Advance to GO
Go to JAIL
Chance (10/16 cards):
Advance to GO
Go to JAIL
Go to C1
Go to E3
Go to H2
Go to R1
Go to next R (railway company)
Go to next R
Go to next U (utility company)
Go back 3 Squares.
The heart of this problem concerns the likelihood of visiting a particular Square. That is, the probability of finishing at that Square after a roll. For this reason it should be clear that, with the exception of G2J for which the probability of finishing on it is zero, the CH Squares will have the lowest probabilities, as 5/8 request a movement to another Square, and it is the final Square that the player finishes at on each roll that we are interested in. We shall make no distinction between "Just Visiting" and being sent to JAIL, and we shall also ignore the rule about requiring a double to "get out of jail", assuming that they pay to get out on their next turn.
By starting at GO and numbering the Squares sequentially from 00 to 39 we can concatenate these two-digit numbers to produce strings that correspond with sets of Squares.
Statistically it can be shown that the three most popular Squares, in order, are JAIL (6.24%) = Square 10, E3 (3.18%) = Square 24, and GO (3.09%) = Square 00. So these three most popular Squares can be listed with the six-digit modal string: 102400.
If, instead of using two 6-sided dice, two 4-sided dice are used, find the six-digit modal string.
玩家从 GO 开始,每次将两个六面骰子的得分相加来决定他下一步走向的格子(顺时针方向)。如果没有其他规则的话,可以预料每个格子被访问到的几率是相等的:2.5%。但是,如果落到格子 G2J(去监狱 JAIL),格子 CC(公益金),格子 CH(机会)的话,这个分布就会被改变。
除了 G2J 以及 CC 和 CH 中的一张牌能够让玩家直接进监狱(JAIL)以外,如果玩家连续三次掷骰子得到两个相同的数字,那么第三次玩家也将直接进监狱。
在游戏开始时,CC 和 CH 中的牌是乱序排放的。当玩家落到 CC 或 CH 时,他从相应的牌堆顶上拿一张牌,并执行完下面的指令后,将牌放回到牌堆的底部。每个牌堆中有 16 张牌,但是简单起见在此题目中只考虑涉及到移动的牌,任何不涉及到移动的牌将会被忽略,而且玩家仍然将处于 CC/CH 格子上。
这个题目的核心问题是每个格子被访问到的可能性。也就是每次掷骰子之后落到某个格子的几率。因此,除了落到 G2J 的几率为零以外,落到 CH 的几率最小,因为落到 CH 后有 5/8 的几率会再次移动到其他格子。而我们感兴趣的是每次掷骰子之后最终落到的那个格子。我们对“只是访问”和被送到 JAIL不作区分,我们也同时忽略需要掷一个 double(两个相同的数字)才能走出 JAIL 的规则,只是假设玩家下一轮自动走出监狱。
从 GO 开始对格子编号(00 到 39),我们将这些两位数的数字相连接来得到与格子的集合相对应的字符串。
从统计上来说可以得到三个最受欢迎的格子按顺序是,JAIL(6.24%)= 10,E3(3.18%)= 24 ,GO(3.09%)= 00 。所以这三个最受欢迎的格子可以用一个六位的字符串表示:102400。
如果我们用两个 4 面的骰子代替两个 6 面的骰子,找出代表三个最受欢迎格子的六位字符串。
回想起上次被54题的扑克牌支配的恐惧...
所以我决定粗略说说思路就行了;模拟题,顾名思义难点和有趣的点都在将题中涉及的流程模拟出来,本题也是,模拟出玩家在每格对应的行动,使用随机函数不断进行游戏,最后统计落到每个格子的概率即可,模拟的流程题设就按题设来即可. 不放代码了..
ans:101524

Counting rectangles
Problem 85
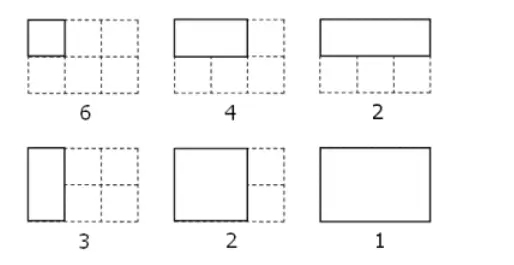
By counting carefully it can be seen that a rectangular grid measuring 3 by 2 contains eighteen rectangles:
Although there exists no rectangular grid that contains exactly two million rectangles, find the area of the grid with the nearest solution.
在3×2的网格中放置单个长方形,共有18种放法,图见上。
问最接近2000000种方法的网格的面积。
如果用opt[m][n]来表示m×n网格的长方形放法,那么在脑内粗浅的递推一下可知:
opt[m+1][n]中肯定包含了opt[m][n]的所有放法,且新的放法必定与新多出来的那一行有关
考虑所有在m+1行有方格的放置情况,
不难得出:opt[m+1][n]=opt[m][n]+(n+1)n(m+1)/2
同理: opt[m][n+1]=opt[m][n]+(m+1)m(n+1)/2
存数组,主函数跑一遍即可.
最接近2000000的解法是36×77的网格,有1999998种放法
ans:2772

Cuboid route
Problem 86
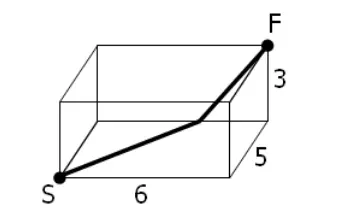
A spider, S, sits in one corner of a cuboid room, measuring 6 by 5 by 3, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest "straight line" distance from S to F is 10 and the path is shown on the diagram.
However, there are up to three "shortest" path candidates for any given cuboid and the shortest route doesn't always have integer length.
It can be shown that there are exactly 2060 distinct cuboids, ignoring rotations, with integer dimensions, up to a maximum size of M by M by M, for which the shortest route has integer length when M = 100. This is the least value of M for which the number of solutions first exceeds two thousand; the number of solutions when M = 99 is 1975.
Find the least value of M such that the number of solutions first exceeds one million.
一只蜘蛛 S 坐在一个 6×5×3 的立方体屋子的一个角落里,一个苍蝇 F 坐在与之相对的角落里。如果只允许在屋子的表面行走的话,从 S 到 F 的最短“直线”距离是 10,路线在图中标出。
但是,每个立方体都有三条可能的最短路径,而且最终的最短路径并不一定是整数。
考虑所有整数边长的立方体屋子,最大不超过 M×M×M,当 M=100 时一共有 2060 个立方体的最短路径是整数,而且这也是解超过 2000 的最小的 M;M=99 时又 1975 个立方体的最短路径是整数。
找出最短路径整数解个数超过一百万的最小的 M。
......BF选手已就位;
对每个a×b×c的长方体先找到3个路径中最短的那条,检验是否为整数解..
3个路径的平方:
a * a + (b + c) * (b + c);
b * b + (a + c) * (a + c);
c * c + (a + b) * (a + b);
为了不重复找b>=a,c>=b
实际上这题应该用勾股数生成公式先跑出所有的整数解再计数的...
但最原始的暴搜也不慢
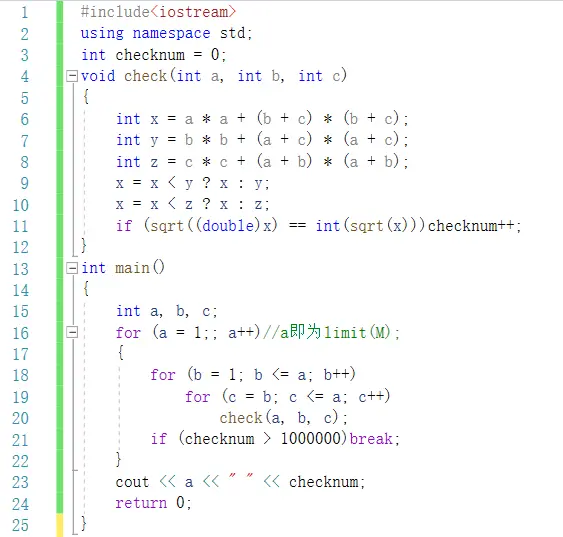
结果为M=1818时有1000457个整数解
ans:1818

Prime power triples
Problem 87
The smallest number expressible as the sum of a prime Square, prime cube, and prime fourth power is 28. In fact, there are exactly four numbers below fifty that can be expressed in such a way:
28 = 2^2 + 2^3 + 2^4
33 = 3^2 + 2^3 + 2^4
49 = 5^2 + 2^3 + 2^4
47 = 2^2 + 3^3 + 2^4
How many numbers below fifty million can be expressed as the sum of a prime Square, prime cube, and prime fourth power?
最小的能写成质数的 2,3,4 次方之和的数是 28。50 以下一共有 4 个数可以写成这种形式
5000 万以下的数中有多少个能写成一个质数的 2 次方,一个质数的 3 次方和一个质数的 4 次方之和?
简单的暴搜. 50000000把以内的质数的2,3,4次方都找出来,记录并计数所有可能的和即可
因为根号50000000为7071+,所以质数表只需要跑到7071即可
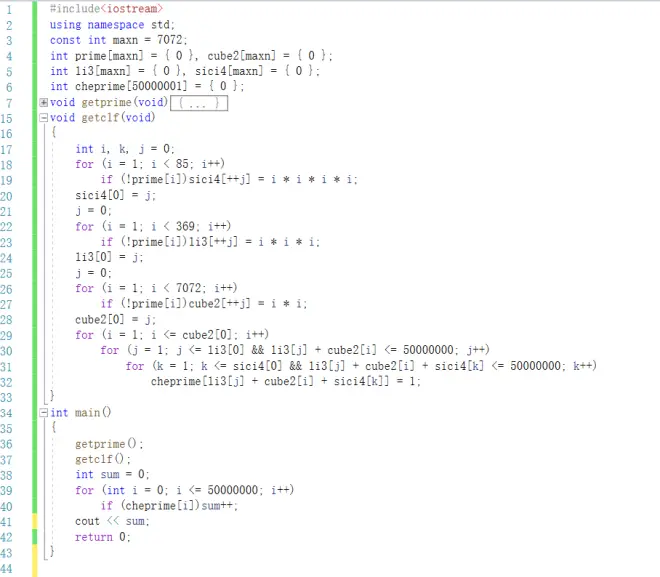
ans:1097343

嗯.偏水的一期(35% 15% 35% 20%)(明明不算低但连BF都能轻易过...)
随缘更新后续.

