【菲赫金哥尔茨微积分学教程精读笔记Ep130】指数函数的函数特性

今天开始看一些函数对应的函数方程以及证明。

75指数函数、对数函数及幂函数的函数特性

a.指数函数（f（x）=a^x（a>0））对应的函数方程：f（x+y）=f（x）*f（y）

非零（除去f（x）=0的情况）：确定值域——

1. 除去f（x）恒为0的情况，即存在x0∈R，f（x0）≠0；

2. 则对任意x∈R，f（x0）=f（x）*f（x0-x）≠0，即对任意x∈R，f（x）≠0.

恒为正——

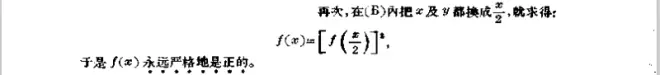
1. 对任意x∈R，f（x）≠0；

2. 由1：f（x）=f（x/2）f（x/2）=[f（x/2）]^2>0，即f（x）永远为正。

验证方法都是利用Ep129的我们已经验证过f（x）=cx（c为常数）对应的函数方程f（x+y）=f（x）+f（y）——

1. 已知函数方程：f（y1+y2）=f（y1）*f（y2），则ln f（y1+y2）=ln f（y1）+ln f（y2）；

2. 令g（x）=ln f（x），由1：g（y1+y2）=g（y1）+g（y2）；

3. 由Ep129知：g（x）=cx（c为常数），则ln f（x）=cx，f（x）=e^（cx）；

4. 令a=e^c，则f（x）=a^x，证毕。

到这里！