工程制图点的投影练习
1、已知各点的空间位置,画出其投影图(尺寸由立体图量取,并取整)

编辑切换为居中

编辑切换为居中
2、已知点的一个投影和下列条件,求其余两个投影。
A点与V面的距离为20mm。
(2) B点在A点的左方10mm。
编辑切换为居中

编辑切换为居中
3、已知点A(35、20、20),
B(15、0、25),求作它们的投影图。

编辑切换为居中

编辑切换为居中
4、已知各点的两个投影,求作出第三投影。

编辑切换为居中

编辑切换为居中
5、判断下列各点的相对位置。

编辑切换为居中

编辑切换为居中
6、已知点B在点A的左方10mm,下方15mm,前方10mm;点C在点D的正前方10mm,作出点B和点C的三面投影。

编辑切换为居中

编辑切换为居中
7、已知A点(10,10,15);点B距离投投影面W、V、H分别为20、15、5;点C在点A左方10,前方10,上方5,作出A、B、C的三面投影。

编辑切换为居中

编辑切换为居中
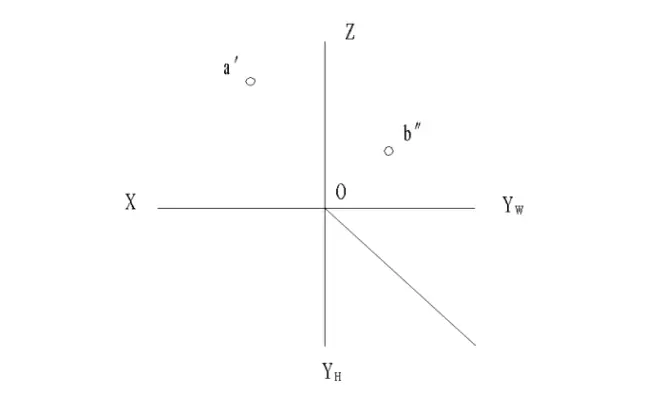
8、已知点A到H、V面的距离相等,求a′、a″。如果使点B到H、V、W面的距离相等,点B的三个坐标值有什么关系,作出点B的各投影。

编辑切换为居中

编辑切换为居中
9、判断下列各直线对投影面的相对位置,并画出三面投影。

编辑切换为居中

编辑切换为居中
10、过点A作线段,使其满足下列各条件(讨论:下列各题有几解,只作出一个解)。

编辑切换为居中
编辑切换为居中
11、求线段AB的实长及其与H、V面的倾角α、β

编辑切换为居中
知识点:直角三角形法求直线的倾角及线段实长。
1、分析: 1)根据用直角三角形法求解直线与投影面的倾角及其线段的实长过程可知,在由线段两端点的Z坐标差和线段的水平投影长为两直角边的三角形中,斜边等于线段的实长,斜边与水平投影长的直角边的夹角等于α;
2)在由线段两端点的Y坐标差和正面投影长为直角边的三角形中,能够反映线段与V面的夹角和线段的实长。
3)由投影图中可知,线段的水平投影长、正面投影长,线段两端点的Y坐标差和Z坐标差均可通过作图求得。
2、作图步骤: 1)过a′,b分别作水平线,二直线分别交bb′连线和aa′连线于点1和点2;
2)过点a′作a′b′的垂线,过点b作ab的垂线;并分别在二垂线上截取a′A1=a2(ΔYab),bb=b′1(ΔZab)
3)用线段分别连接b′A1和aB1;结果如图所示。
编辑切换为居中
12、在物体的投影图中标出AB、BC、CD各棱线的三面投影。
编辑切换为居中
编辑切换为居中
13、完成AB的三面投影,并在AB上找一点K,使点K到H、V面的距离相等。
编辑切换为居中
知识点:直线的投影;点到投影面的距离与坐标的对应关系;直线上点的投影。
分析: 1)侧面上:OZ轴是V面的积聚投影,OYw轴是H面的积聚投影;
2)由点K到H面、V面的距离相等,既ZK=YK,则点K一定在H、V面的角等分平面上,该面的侧面投影为OZ、OYW轴的角等分线;
3)该等分角线与a″b″的交点k″即为AB上到H、V面的等距离点。
答案见下图:
编辑切换为居中
14、求线段CD的实长及其与V面的夹角β。
编辑切换为居中
知识点:直线的投影、实长及其与投影面的夹角。
提示: 1)c′C1=c″1;
2)∠C1b′c′=β;
3)C1d′即为实长。
答案见下图:
编辑切换为居中
15、求ΔABC的实形。
编辑切换为居中
知识点:直线的投影、实长;三角形的实形。
1、分析: 1)由初等几何可知,已知三角形的两边及其夹角、两角及其夹边或三边(实长)均可作出某个三角形。现根据ΔABC的水平和正面投影可知,AC为水平线,其水平投影反映线段AB的实长,即ac=AC;同理,a′b′=AB。只要再求出BC 的实长,ΔABC便可作出。 2)利用习题1-11的方法求出BC的实长。 3)以线段ac、a′b′和b′C三边作出ΔABC;ΔABC即为所求。
2、作图步骤: 1)过点b作ox轴的平行线,该线交cc′于点1; 2)过c′作直线垂直于b′c′,在该线上截取c′C1=b1; 3)用线段连接b′C1,b′C1即为BC边的实长,即b′C1=BC; 4)分别以点a、c为圆心,以a′b′、b′C1为半径画圆弧,二圆弧交于点B;用线段连接点a、B和点cB,则ΔaBc≡ΔABC 。
编辑切换为居中
16、已知线段AB与V面的夹角β=30°,求其水平投影。
编辑切换为居中
知识点:已知直线的一个投影长度和其与投影面的一个夹角,利用直角三角形法求得第三个坐标的差,从而求得直线的其它投影。
在用直角三角形法求解线段的实长和倾角的作图中,其中包含β的直角三角形的三边分别为:斜边→线段实长,β角临边的直角边→线段正面投影的长度,β角的对边→线段两端点的Y坐标差。此时已知线段的正面投影及其β角,则此题易解。
答案见下图:
编辑切换为居中
17、已知线段EF=35mm,其投影e′f′及e″,求EF上的点K的投影,使EK为已知长度L。

编辑切换为居中

编辑切换为居中
18、已知线段CD=45mm,求其正面投影。

编辑切换为居中
知识点:利用直角三角形法求直线的投影。
由于已知线段的实长及其水平投影,故而,在以水平投影为一直角边,以线段实长为斜边的直角三角形中,其另一直角边则为线段正面投影两端点的Z坐标差,

编辑切换为居中
19、在已知线段AB上求一点C,使AC:CB=1:2,求出点C的投影

编辑切换为居中
知识点:点属于直线的性质:点分线段所成的比例固定不变。注意特殊位置直线的比例三角形法的应用。

编辑切换为居中
20、过点A作一实长为30mm的线段AB,它与H、V面的夹角分别为α=45°,β=30°;此题有几个解?

编辑切换为居中

编辑切换为居中
21、在直线AB上求一点C(c、c′),使点C到H面的距离为15mm。

编辑切换为居中

编辑切换为居中
22、判断下列各直线间的相对位置。

编辑切换为居中
知识点:两直线的位置关系——平行、相交与交错。
1、平行条件:a、同面投影平行(含投影重合——共面);b、比例关系不变;c、方向一致。
2、相交条件:交点唯一——投影交点符合点属于直线的性质。
3、交错条件:非平行和相交。
注:当为共面直线时,两线位置只有平行和相交。此时判断:只要看另一投影平行——即两线平行(如1中:AB与CD);非平行——即为相交(如2中:EF与GH;4中:AB与EF)。

编辑切换为居中
23、过点A作线段AB,使AB∥CD,AB的实长为30mm。

编辑切换为居中
知识点:利用直角三角形法求直线的投影及其与投影面的夹角。
AB∥CD即ab∥cd,a′b′∥c′d′,a″b″∥cd″,故,过点a作直线al∥ab,过a′作a′l′∥a′b′则:ab∥al,a′b′∥a′l′。利用直角三角形求线段实长的方法便可得解。
答案见下图:

编辑切换为居中

