【机器人基础】Introduction to Robotics@UCB

在看的小伙伴不要被前面几个视频劝退，P4以后的声音和视频都很好，而且教授改用了手推定理的方式，讲的很好。

Chapter2: rigid body motion

2.2 rotational motions in R3

property of a rotation matrix: orthnornal

rotation matrxi in invitable since the rank is 3 (full rank)

Since orthormal, R-1=RT

(detR)^2=detR*detRT => 1 => detR = +-1

SO(3): othonormal matrix with deg 3 -> a group

group: g1*g2 in G (closure under multiplication)

exists a identity element

all elements have an inverse

Examples of group

R3->addition operation: is a group

0 vector: identity

inverse: negative

(0,1) mod 2 addition

identity: 0

R, multiplication

inverse: 0 does not have -> not group

Property: SO(3) is a group with matrix multiplication

R1*R2 is in SO(3)

identity: I

inverse: RT

Configuration and rigid transformation:

property 2: Rab preserces distances and cross product

R(vXw)=RvXRw

Euler's formula

euler formular for SO(3)

every rotation is a exponential of something

skew symmetric matrices: odd dimention...

9 numbers: only 3 indenpendent parameters

figure what are the 3 parameters

omega_hat is so(3),

hat: R3->so(3), i.e., omega-> omage_hat

exp: so(3)->SO(3), omega_hat*theta->exp(omega_hat*theta)

exponential of a skew symmetric matrix is always a rotational matrix

Rodrigues' formula

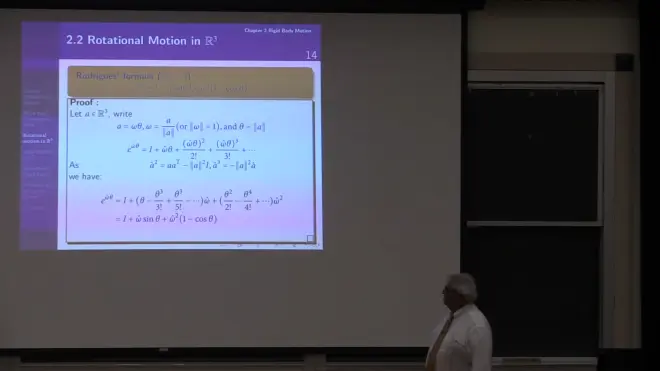
product of two skew sym matrix, is sym