本文译自A. V. Akopyan, A. A. Zaslavsky, trans. Alex Martsinkovsky, Geometry of Conics, American Mathematical Society, 2007.

翻译：野吕侯奈因

仅供学习交流使用

译者按：

本书在几何爱好者之间小有人气，但目前网上只能找到一些零散的翻译. 鉴于目前通行的数学教学中对于二次曲线问题的处理方式过于单一，希望能借翻译本书的机会来推广一下二次曲线的射影几何视角.

前言：

二次曲线，或者说圆锥曲线，通常被视为解析几何学研究的对象而存在于工科专业的低年级授课中．对于其几何性质充其量也就介绍了些光学性质．但这些曲线还拥有更多有用的性质，甚至大部分都是可以建立在高中生就能接触到的初等几何方法上的．此外，二次曲线还可以帮助解决一些看似与其无关的几何问题．在本书中读者将会学习到很多关于二阶曲线非常有趣的知识，其中有些甚至是近些年才被证明出来的．

第一章介绍了二次曲线的一些基本性质，其中大部分性质都是众所周知的，剩下的那部分也很简单，因此整章的内容都没有超出普通高中生的理解能力范畴．一些简单但很重要的结论会被留作习题，希望读者在翻阅解答前能先尝试自行解决，这会有助于对接下来内容的理解．第二章是一些前置性的资料，内容是高中教学中不常提及却被理解后续章节所需要的古典几何学知识．第3章中介绍了二次曲线的一般射影性质，像是二次曲线束的相关定理，也就有些难度了．最后，在第四章介绍了一些度量性质，通常只会在特殊的二次曲线中考虑它们．这也是本书中难度最大的一章，需要建立在充分理解先前章节的基础上阅读． 

作为作者在此感谢I. I. Bogdanov和E. Yu. Bun'kova提供的宝贵意见．

第一章
二次曲线的诸基本性质
1.1. 定义

如果你钉下一根木桩拴住山羊，它吃草的范围就会是以木桩为圆心，绳长为半径的圆．如果你钉下两根木桩系在绳子的两端，再用这条可滑动的绳子拴住山羊，这时他吃草的范围就会变得像图1.1这样．

  与是两焦点；与分别表示长轴和短轴．

在这条上的所有点，其到到木桩的距离之和都等于绳长．这样的曲线叫做椭圆(ellipse)，木桩所在的点叫做焦点(focus)．

显然，椭圆看起来像个“被抻长的圆”，并且明显有两个对称轴，分别是焦点所连直线以及焦点所连线段的中垂线，它们分别被称作椭圆的长轴(major axis)和短轴(minor axis)．它们在椭圆内部的长度叫做长轴长和短轴长，焦点之间的距离被称作焦距．

同样很明显的是，拴山羊的绳长就等于它吃草区域所形成的椭圆的长轴长．

直观上看，很显然山羊可以吃掉在椭圆内的所有点长的草，并且永远无法离开椭圆．但是这个问题的严格的数学转述就不能用显然来一笔带过了．

练习1. 求证：在椭圆内的所有点到焦点的距离之和小于长轴长，在椭圆外的所有点到焦点的距离之和大于长轴长．

解答：用和表示两焦点，任取一点．设为射线与椭圆的交点．先假设点在椭圆内．由三角不等式，有，因此有（图1.2）．

其中就等于绳长，也就是长轴长.在椭圆外时的证明也与之类似，我们有．因此有．

在力学中经常能看到椭圆的身影．例如，行星绕太阳运动的轨迹就是一个也太阳为其中一个焦点的椭圆．（开普勒定律(Kepler's Law)）

椭圆就是一种二次曲线(curve of second degree)，或者说圆锥曲线(conic)．除此之外还有抛物线(parabola)和双曲线(hyperbola)．

双曲线作为到两定点距离之差的绝对值为定值的所有点的集合，这两个定点被称作焦点(focus)．

双曲线由两支渐近于两条直线的曲线组成，这两条直线叫做双曲线的渐近线(asymptote)．两条渐近线相互垂直的双曲线被称作等轴双曲线(equilateral)．

双曲线的两焦点确定的直线是双曲线的一条对称轴，叫做实轴(real axis)．双曲线两焦点所连线段的中垂线也是双曲线的一条对称轴，叫做虚轴(imaginary axis)．（图1.3）

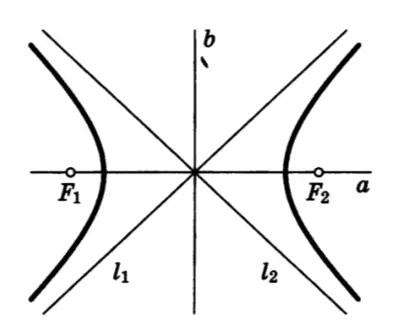
与是两焦点，与分别表示实轴和虚轴，和为两渐近线．

假如有一颗彗星接近了太阳，而太阳对它的引力又过小而不足以支持它进入太阳系，那么这颗行星的轨迹就会是一支以太阳中心为该支焦点的双曲线．

（译者注：实际上，彗星绕日运行的轨迹只能为二次曲线．）

抛物线作为到一定点和一定直线距离都为相等定值的点的集合，其中的定点和定直线分别被叫做抛物线的焦点(focus)和准线(directrix)（图1.4）．

经过焦点引一条准线的垂线，即为抛物线的轴(axis of the parabola)．

显然，它就是抛物线的对称轴．

（译者注：中文里好像都没有这种叫法？）

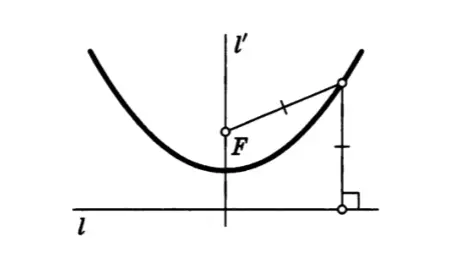
为焦点，与分别为准线和抛物线的轴．

我们可以注意到，如果以某个角度投掷出一枚石子，石子正好会沿着抛物线运动．

另外，从几何观点上看，抛物线只存在一种形态（就像圆只存在一种形态一样）．更准确地说，一切抛物线都相似，即任意抛物线都可通过旋转位似变换转化为另一抛物线．

（译者注：关于抛物线和圆都只存在一种形态这一性质之间的联系，聪明的读者可能会想到圆锥曲线静态的原始定义：以一平面截一圆锥面，当平面与圆锥的轴垂直时，截面图形为圆；当平面平行于圆锥母线时，截面图形为抛物线．至于进一步的说明，只需要用一种构造性的方法构造出一个由所有圆或抛物线平行排布出的椎体即可．）

现在来考虑一系列椭圆，它们拥有同一个焦点并且经过同一个定点．我们让另一个焦点不断趋近于某个方向上的无穷远处，那么这个椭圆也就会不断趋近于一个拥有同一焦点，其轴平行于该方向的抛物线。我们同样可以对双曲线做类似的操作．因此抛物线实际上是椭圆和双曲线的极限情况．

练习2. 请叙述并证明：对于抛物线和双曲线，都有与练习1类似的结论．

解答：对于抛物线内的点，其到焦点的距离小于到准线的距离，抛物线外的点则反之（图1.5）．

设为在准线上的投影，为与抛物线的交点，用表示抛物线的焦点．由抛物线的定义，有．若位于抛物线内，则有．由三角不等式，有．若与抛物线分居准线两侧，则点在抛物线之外时的结论显然成立．若在抛物线之外而与抛物线位于准线的同侧，那么有，且由三角不等式，有．故可得．

对于双曲线，结论则如下所述：设为双曲线上任一点到两焦点和之间距离之差，设为所在支的双曲线．则对于在之外（内）的点，都有的值小于（大于）．（图1.6）

当在之内时，设为与的交点．则有．由三角不等式，有,因此可得．

若在之外，设为与的交点．则有．由三角不等式，有．因此可得．

我们可以注意到（证明先卖个关子）无论是椭圆，抛物线，还是双曲线都有以下性质：平面内任一直线至多与该曲线交于两点；任取平面内一点，至多可引该曲线的两条切线．这些性质也只是1.5节中结论的显然推论．

练习3. 试求两定圆其公切圆圆心的轨迹．

解答：为了使问题更加具体，先考虑这两个以、为圆心，、为半径的圆外离时的情况．若这个以为圆心，为半径的公切圆与两圆都外切，则有及，可得，即会落在以为两焦点的双曲线的一支上．类似地，若公切圆与两圆都内切，则会落在该双曲线的另一支。若公切圆与其中一个圆内切并与另一个圆外切，则有，即此时落在焦点相同的另一条双曲线上．同样，若存在一圆内含于另一圆的情况，则所求轨迹则可能出现两种以为两焦点，或为长轴长的椭圆的情况．至于两圆相交的情况，就留给读者思考了．

（译者注：两圆相交的情况与外离的情况类似：公切圆与两圆都外切时，在以为两焦点，为实轴的双曲线的一支在圆外的部分上；公切圆与两圆都内切且公切圆内含于两圆时（当然，两圆相切时不会出现这种情况），在该双曲线的相同支在圆外的部分上．公切圆与两圆都内切且两圆都内含于公切圆时，在该双曲线的另一支上．另外，书中也有些情况没有提及，比如当两圆半径相等时，无论两圆的位置关系如何，都会落在所连线段的中垂线（当然，不包括切点或者两圆交点）上；而当两圆内切且公切圆与两圆都外切时，则会落在或到两圆切点方向的射线在两圆外部的部分．可能对这个问题研究得最透彻的还得属中等教育界人士吧（笑）．）

译后记：

本段和紧随其后的1.2可以说是全书中最贴近高中教学的部分了．原以为这两段存在的意义是照顾没有学习过圆锥曲线的读者，读后却觉得更像是面向学习过圆锥曲线的读者来巩固知识．本段使用了很多并不是那么严谨的“注意到”、“显然”等字眼，想必也是默认读者接触过相关知识吧．本段有一个在我看来相当精妙的比喻，就是引入椭圆时提到的山羊吃草，起初还没太参透为什么要这么比喻，直到看到后面讨论点在椭圆内外跟与焦点距离之和的关系才恍然大悟．在我看来本段的写作特点也是如此，在保持了其通俗易懂的同时没有放弃作为一本数学教材应有的细致与准确．