QFT#0

这学期选修量子场论,课上随便记点东西。将就看吧。主要只记个大致思路。
(因为基本上就是上课时间记的,课后只作简单整理)
这是南开大学物理科学学院专业选修课量子场论,授课教师是李佟老师。

话说这量子场论本来是研究生课程,后来对本科生开放,试着来学学。
首先是一些符号、约定上的准备工作:
自然单位制:
, 量纲相应简化为
狭义相对论:
,知道意思就好
使用爱因斯坦求和约定。

QFT 简介
QFT : QM + SR (量子+狭相)
量子场论处理无穷自由度,粒子是场激发后对应的量子。
进而可以发展量子多体理论和粒子物理与标准模型两个方向。
QFT可以处理粒子数改变的过程。
教材:Peskin
接下来有一些历史回顾。
相对论波动力学:QFT之前的早期尝试,失败,原因:
负能解问题?负几率问题?(相对论中ψ²不正定)破坏因果律?
如果试图推导相对论性波动力学,考虑
各量替换为相应算符,
得到Klein-Gordon方程:
猜平面波解
能量本征值出现负能解: 真空不稳定?
另:由于时间二阶导的存在,出现负几率的可能?

解决:Dirac.
尝试把方程重新降为时间一阶导数。
必须把原来的波函数扩展成列矢量。普通的微分方程变为含矩阵微分方程。
引入待定矩阵,令方程为
(因为直接开方没法开,所以每个α,β必须都是矩阵)
期待该方程平方后能重新得到K-G方程。
经过一系列计算,发现这些都应该是四阶方阵,它们定义为gamma矩阵(详细内容参看高等量子力学)
于是最后得到狄拉克方程:
狄拉克方程仍有负能解,提出狄拉克海,把真空看作负能级填满的海,激发真空产生的空穴就是正电子。
好吧,即使有狄拉克的这些操作,有些东西还是有点怪怪的...
事实上狄拉克海当然也是不存在的,但是真的有正电子。
另外,狄拉克方程可以推出自旋,成功解释氢原子能级的精细结构。(但不能解释兰姆位移和电子反常磁矩)
(QED辐射修正可以解决电子反常磁矩)
(兰姆位移也可以在QFT框架中得到解释)

破坏因果律的问题:固定粒子数的量子力学总是破坏因果律。
因果律的本质来自Lorentz对称性,在狭义相对论和量子力学结合的框架下必须引入“反粒子”。
*反粒子 *自旋-统计定理

QFT利用场的概念,将经典场量子化的概念突破固定粒子数的限制,可以描述无穷多自由度。

量子场论的诞生
首先来一个toy model,演示如何进行场量子化。这是场量子化的一个基本操作流程。
考虑一个一维经典弦,它可以看作微小质量元和小弹簧交错分布的连续弹性体。
设弦在t,x处的位移 . 弦的线密度、杨氏模量分别为 μ,T.
经典力学会给出这样一个弦的拉格朗日量:
重新整理一下,把长 l 的弦两端固定,并且重新定义,
考虑把解展开为傅里叶级数,是常规操作。
频率是量子化的,从而可以满足边界条件。把这个形式的解代回拉格朗日量和哈密顿量,是这个形式:
正则动量定义为:,于是
已经和谐振子哈密顿量很接近了,接下来类比量子力学里面单谐振子的量子化。
量子化,要求 (基本对易式)
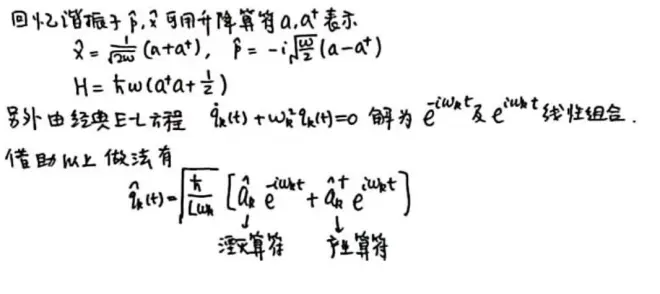
像这样量子化的一维弦的本征态可以写作
意思是说频率 ω_k 的光子有 n_k 个。
意义:的存在(产生、湮灭算符)可以改变粒子数。QFT核心特点之一。
这里也有真空能

