大学物理(电磁学)知识梳理与例题选讲:§04 电介质

极化现象
# 概念
## 绝缘体中存在束缚电荷
## 极化(极性分子):电偶极子极矩不为0

外加电场下会发生的极化类型
- 位移极化(非极性分子在外电场作用下,正负电荷发生位移偏移而产生的极化)
- 取向极化(本为极性分子,在外加电场下极矩方向将变为与外加电场方向相同)
注意区别:导体的静电平衡与极化电荷
- 导体的静电平衡是电荷会在导体表面,电荷为自由移动,可以完全抵消外电场亦保持静电平衡
- 极化电荷:其为绝缘体电荷不发生自由运动,只发生极化(电子在原子范围内运动),内部的电荷与附近电荷相抵消,从而只有本来就在表面出的电荷起到作用,进而只能削弱外电场的影响
### 极化强度P:电偶极矩的体密度,为一个矢量

极化电效应
# 概念

注意
- 注意:极化电荷的场强 $E_{p}$,自由电荷的场强为 $E_{f}$
- 区别极化电荷与电势的符号,极化电荷为矢量,电势为标量
- 均匀介质的式子中的 χ 不是字母x,而是$\chi$(/kai/),P为极化强度
- 极化强度P的面积分中,即极化强度的通量(注意极化强度通量结果应改为 $-Σq_{in}$)

# 绝缘体极化电荷的表面性质
- 极化电荷面密度 $σ_(p}$(可为正负)

- 电位移:极化强度的通量与高斯定理推论的量

转化为只与自由电荷有关的式子

可得新的量——电位移D与其子表达式

电位移D的通量:电介质的高斯定理

注意:电位移D仅为一个定义量,而无物理意义(目前2017,up主说)
## 关系谱图与关系推导

注意此时电位移D不一定等于 $ε_{0}E_{f} $

### 在下列状况下等式成立
除了导体球外,其余空间充满电介质;或者对称导体内部充满电介质后对称性不改变时(而外部空间为真空)亦可满足等式

当满足电位移的推导等式成立时,有

推导得

此时,极化电荷的场强值 $E_{p}$ < 自由电荷的场强$E_{f}$,从而有总场强E只是被极化电荷场强削弱了

电介质问题简析
# 关系谱图
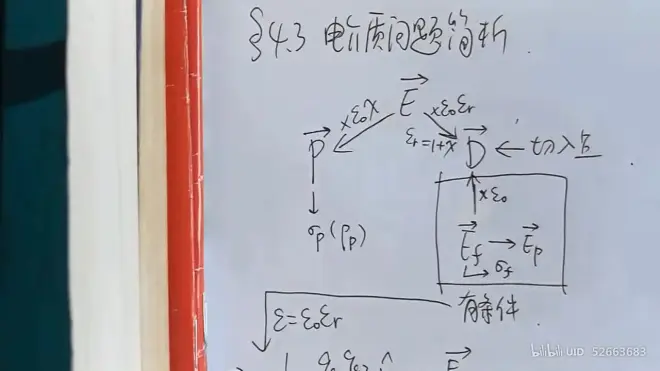
## 区分自由电荷与极化电荷
- 自由电荷:人为添加的或者为导体感应而产生的
- 极化电荷:原先属于电介质洞中的,在极化过程中所体现而出的
## 电位移等式成立时的定律
- 库仑定律

- 电容器与电势

- 电能密度

## 通量整理

### 电介质内外(界面连续问题)

# 例子
## 例1:极化电荷的面密度
已知球形空腔的半径为R,内部的电荷为q,求介质的极化电荷的面密度 $σ_{p}$

区分在球表面与球外部空间的电位移D与场强E

分别得到极化强度P在球面与外部的表达式

求出极化电荷面密度 $σ_{p}$(注意:法向量为介质的外法向,因此其朝向空腔内部)

极化电荷 $q_{p}$

## 例2:平行板电容器内部充满电介质
求极化电荷q_{p}

思路与结果应该与上例一致
## 例3:多区域电介质的电容器问题

可将其当作电容器的串并联
- 并联电容器

- 串联($ε_{2}$ 和 $ε_{3}$)

## 例4:电介质运动问题
图中标出皆为已知量,求电介质的位移x与电场力F的关系式

由能量守恒,可得(分情况表达式的求解思路)

界面连续性
# 界面连续下的性质
## 法向分量

### 极化强度P(界面连续下)

突变量 $σ_{p}$(注意上图式子中的外法向的方向)

### 电位移D(界面连续下)

突变值(注意:与界面连续下的极化强度P的突变值相区别)

#### 特殊情况
- 没有自由电荷时 $σ_{f}$

## 切向分量
### 电场强度E
由环路定理,可得

### 电位移D

# 界面介质的折射定律

由界面连续的法向与切向的性质,可得

- 当自由电荷 $σ_{f}$ 为0时,有


