连续与离散随机变量边缘分布函数的不同

连续与离散随机变量的边缘分布函数的计算方法有所不同。先看两者的定义：

由图1和图2可以看到，连续型变量的边缘分布是一个积分，比如x的边缘分布，x本身的变化是一个范围；而离散变量x的边缘分布，x则是一个固定值xi，这是一个重要的区别。

将图1与联合分布函数的定义图3对比：

可得到：如果

举例如下：假设

其中

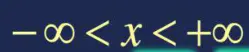
再看离散变量的边缘分布：

求被调查者吸烟的条件下得肺癌的概率和不吸烟的条件下得肺癌的概率：

由上图可以看到，当求x=1时候的边缘分布的时候，并没有像连续型变量一样，把x=0时候的概率叠加进去。

由上图也可以理解这样规定的原因：因为x=0和x=1代表两种截然不同的情况，如果叠加的话就变得毫无意义。

简单总结：

1：连续型变量的边缘分布函数是一个范围的积分，离散型则是一个固定值；

2：连续型变量既有边缘分布函数，也要边缘密度函数；离散型则只有边缘分布，没有边缘密度。

3：由于边缘分布函数是一个范围积分，因此，可以把离散型变量的某一个取值看作是一个区间，而不是一个点。