【西北工业大学】微波技术与天线

看到
电磁波的故事

这是麦克斯韦方程组,第一个 M是磁单极流,暂时没有。

------------------------------------------传输线理论
微波传输线一般都是长线,比较复杂,需要用分布参数。一般长于波长的10分之一就是长线。
集总参数lumped parameter。
微波长线都是用分布参数。
注意:分布参数的单位由于是均匀分布的,和传输线长度有关,所以一般单位都要加上 /m,如 欧姆每米。
研究传输线,主要是为了研究分布沿线的电压和电流分布。

基尔霍夫定律得到关于电压和电流的定律

让德尔塔Z趋于0,然后除德尔塔Z,就得到了下面的式子。
think:有意思的是,这里电压和电流与电感,电容电阻,电导有关。如果这里这些都为0,则电压电流的变化也是0。而不是由波本身的传播导致的。
为了解这个方程,就要分离变量。分离变量后可化简


这就是亥姆霍兹方程或者波动方程,或者叫电报方程。注意γ平方。

这是通解,向两个方向传播的组合构成。

可以看到,Z0由分布参数和频率确定。
think:但是3.15a/b参数完全一样,为什么会差一个参数?
注意:Z的量纲是欧姆/米。Y的量纲是西门子/米(1/欧姆 每米),而不是互为倒数。所以伽马的量纲是1/M。Z0的量纲是欧姆。
U(z)是解方程求出,I(z)是由3.14a式求出。所以这里的Z0就是Z/γ,所以可以得出是根号Z/Y。
另外γ = α+jβ 这两个参数后面会用到。注意,当α不为0,就会指数下降。
think:老师的讲解很棒,其实对于整体无法把握时,就可以看一个小的微元,通过对微元的分析,得出结论,然后利用数学已有的结论知道整体

这里取了实部。
这是最后带时间的通解的形式,现在就剩下U+,U-怎么确定,这需要边界条件。

三组中的任意一组都可以。

同一种颜色的一组就可以。
这里最重要的就是Z0,γ。都是由RLGC这些分布参数来的,这些又是由微波传输线的结构和材料参数来的。
think:RG同意理解,LC和介电常数和磁导率有关,这又是为什么,这个就没理解了。这部分可能还要回电磁学里找答案。

这是直接给出的结果,在这门课里用的不多。
-----------------------------------传输线参数Z0
Z0 特性阻抗。γ传输参数。

这是很重要的式子,U+,I+是入射电压,电流,U-,I-是反射电压,反射电流。负数是因为反射电流方向相反。

大部分情况下,都可以认为R,G=0. 很多地方不区分Z0,Zc,只要说导线就认为无耗。
对比上面的表可以发现,无耗情况下L/C才是μ/ε。(貌似算错了)LC就是μ/ε。

这里算着不对啊?
------------------------------------------------γ


单位rad/m

α是衰减,β是每前进一米,变化的相位角。
---------------------------------相速度与波长

就是应用两个参数的定义。
---------------------------------输入阻抗和反射特性

这里介绍了反射波的本质。导线上U+和I+的比值是Zc,这是无法改变的。
负载的UL和IL比值是ZL,也是无法改变的。这就导致,导线传过来的电压和电流,电压进去,电流就无法全进去,电流进去了,电压就无法全进去。所以就会由部分反射。
实际上既不会电流全进去,也不会电压全进去,而是各反射一部分,可以用下面的方法求出反射多少。
think:至于反射的是电压还是电流不重要,因为在导线的波上,这两者是互相转化,一直改变的。
可以根据这么几点列个方程。
Zc=U+/I+
Zc= - U-/I-
ZL=UL/IL
I+ - I- = IL 这里电流是反向,所以为负。
U+ + U- = UL 这个是看了解释改的,课程的实际解决方法,和我的想法类似。
在这里,Zc,ZL都是固定的,U+是驱动电压也是给定的。那么求I+,U-,I-,UL,IL,要5个方程。

这是视频列的式子。
think:另外从这里可以看出,如果ZL=0,电压全反射,如果ZL=无穷,电流全反射。另外不管是什么波,只要介质不连续都会产生回声。其他波和介质,也有类似于电阻的东西。
这里特别重要。
--------------------------------------输入阻抗Zin

特性阻抗和输入阻抗的对比,注意U(z)和I(z)见前面的波动方程通解。是 U+ + U- 和I+ 加I-。
此外,Zin是z的函数。可以从传输线的任一点往前都认为是输入,这点的阻抗就是输入阻抗。
think:这里用输入阻抗好像也可以求出反射和入射U,I。
在传输线上,分离时间部分

得到

这个之前求过,是从负载端向前定坐标的电压和电流。就可以求出

如果无耗,那么γ就是纯叙述jβ

这个式子非常重要,主要用来算传输线上任一点的输入阻抗。需要背下来。(也有些人管这叫传输线阻抗,只有z‘=l时是定义为输入阻抗。)
β和频率有关。
输入阻抗是负载阻抗的延申,就是负载阻抗,加上其伸出的两个臂影响后的总负载。
---------------------------------------反射系数Γ

以后说反射系数,默认指电压反射系数。
其和位置有关,且是复数。因为U就是有幅度有相位。模值属于[0,1]。

Γ(0)是负载初的反射系数。
在这里反射系数的相位变化速度,也叫相速度变成了电压波的两倍。
think:这里U+和U+(z)注意区分。一个是固定系数,一个是与距离有关的函数。解出的是U+e^jβz' 是系数乘一各随距离变化的相位(无耗情况下)。Γ定义时就是拿这个带z的U定义的。(但为什么要这样?)

这里Γ是z的函数,只是简写了。Zin和Γ是一一对应的关系。这就是网分仪测量阻抗的原理,通过反射系数计算阻抗。
think:反过来,也就可以求反射系数了,比如自己一直想知道的,70欧负载线,在50欧输入阻抗下,反射系数是多少(很容易算出是1/6)。
------------------------------------主要就是这些参数
特性阻抗Z0,输入阻抗Zin(z’),负载阻抗ZL,反射系数Γ(z')。

这是互相的转换关系,这几个式子是最重要的。
think:这些推导有点麻烦,却又不是特别技术,而且形式有点复杂,尤其是Zin,确实不好记。
---------------------------三种传输线状态
追求的目标:行波状态。
负载等于特性阻抗,或者传输线为半无线长时。
全反射时:纯驻波状态
短路,开路,纯虚数 也就是ZL的值为0,无穷,aj
现在研究终端短路为例:
ZL=0,套入3.59,就知道ΓL=-1


3.57是之前得到的,把负载条件带进去,就可以知道电压电流分布。
在这里会发现,电压和电流相位差90°,所以无法做功。

短路下的输入阻抗。

这里输入阻抗,是虚数,系数大于0是感性,系数小于0,是容性。
到4分之一波长时,从0到无穷大。
由于是看幅值,所以电压电流的周期都是λ/2. 而电压波腹的时候,电流在波节,所以这时候输入电阻可以算出是无穷大,其他类似。
以0到λ/4部分为例子,电压在下降,电流还在上升,所以这里电压相位超前电流,所以是感性。反过来,在λ/4到λ/2部分,电流在下降,电压还在上升,所以电流相位超前电压,所以是容性。
think:但是不理解的是这里只是模值啊,比相位的时候不是看的实际值么?
确切的说,应该看Zin的表达式。电感元件的复阻抗Z=jωL。电容元件的复阻抗Z=1/jωC=-j1/ωC。
顺便说下行波状态下,|U|,|I|,|Z|振幅都是直线。这时候,Zin 就是ZL就是Zc。
而对于其他纯驻波,不管是开路,还是纯电感,纯电容,其实都是这幅图的平移。就是把某一点的输入阻抗,当作负载阻抗就可以了。
有了这点,电感电容就可以随意变了,甚至开路短路都可以随意变。
-------------------------------------行驻波状态
传输线终端接的是任意复阻抗

还是用

开始推,求模值和相位,形式会比较复杂。结合3.57可以求出
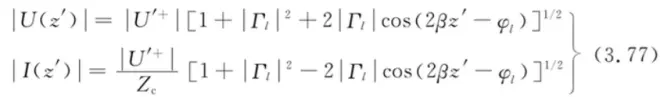
图形为

图形其实很容易理解,也是位移问题。
另外,纯电阻为什么电压和电流不是同时到达最大值? 注意,这是幅值,不是某以时刻的实际值。最大的区别就是行驻波状态下最小值无法为0。还是两个反向波的叠加问题。
最大值和最小值

变换长度还是λ/4,周期还是λ/2。ΓL的模值是不会变的。
ΓL的值在[0,1]之间,数字太小。
定义:


也就是Umax/Umin 显然都是大于1的数。和ΓL一一对应。


这是接感性负载的阻抗实部R和虚部曲线。
具体的R和X的形式就不记了。注意,整个阻抗变化的过程,是开始感性,到纯电阻极大值,然后变容性,到纯电阻最小值。和之前类似,只是开路变大电阻,短路变小电阻。


这个K叫行波系数,用的不多。
一个尝试:使用开槽波导测量终端阻抗。


这是测到的Umax,Umin,和最小值(待测负载)或0点(短路)位置。
多次使用上面的知识,方法很巧妙,具体不再记录。

应用这条之前用过的公式,就可以求出ZL。
think:β多次使用,再次强调,其是γ的虚部,表示的是每米改变多少相位角。由上面的z的间隔可以知道波长λ,进而求出β。
--------------------------------------------------圆图
首先需要强调,输入阻抗是沿线变化的,与他对应的反射系数也是沿线变化。

反回来,负载阻抗和特性阻抗就知道反射系数

这是一一对应关系。

反射系数的模值其实是不变的,只是相位在沿线变化。这个之前讲过了,也要背。
这些计算大都挺麻烦,为了简化计算,史密斯开发了圆图。

是图形辅助计算工具,分开来看。
1,等反射系数圆,反射系数模值相同的圆,反射系数模值相同。只要确定负载和特性阻抗的值,就可以唯一确定平面上的一个等反射系数圆。
think:而这个改变相位角通过改变传输线的长度就可以实现。

等反射系数圆是一族同心圆,而一个Γ和一个ρ又是一一对应的。最外圈Γ是1,ρ是∞大。由于特别容易用圆规画,所以经常不展现在圆图上。沿着传输线走,就会在等反射系数圆上绕圈,方向顺圆逆载
---------------------------------------归一化阻抗圆图

其中

z也可以分解为实部和虚部

一番整理,会发现这里又是两族圆。
不同的r和x对应不同的圆心和半径。
观察3.117a 不同的r产生不同的圆,这些圆都在实轴上。每一个圆,r相等,所以也叫等电阻圆。
3.117b也就称为等电抗圆。
合一起叫归一化阻抗圆。
3.117a无论r取什么值,Γu=1,Γv=0都成立,所以都过此Γu=1,Γv=0的点。结合圆心在实轴上,这些圆也就可以直接画出来了。
同理,3.117b圆心在Γu=1这条线,且也必过点Γu=1,Γv=0的点,也能直接画。

这是归一化等电阻圆,圈越大,r越小。r等于0时,等电阻圆就成了单位圆。r等于无穷大的时候,等电阻圆就成了(1,0)位置的点。
随便一个反射系数点,就可以读出他的归一化阻抗实部,就是看哪个等电阻圆穿过它。

--------------------------------------归一化等电抗圆

有意义的只有单位圆以内的部分,当然根据3.117b 这里的半径可以到无穷大。x越小,半径越大,实际可能穿过Γv>=0的整个半平面。
此外,对于x,也就是虚数的系数大于0,原点在Γv>0的地方,等电抗圆曲线穿过正半平面。
对于x,也就是虚数的系数小于0,原点在Γv<0的地方,等电抗圆曲线穿过负半平面。
所以正半平面对应电抗>0,也就是感性。负半平面对应电抗<0,也就是容性。

对应的方程

画在一起就是史密斯圆图了。
史密斯圆图的一些解读练习,哪边短,哪边开等等。

各个部分,包括顺时针,逆时针的电长度标记,下面的驻波系数,最外层反射系数刻度,稍内层Γ相位(开路时反射相位和入射相位相同,短路时相位相反)标记, 等等。
介绍一个例题,

可直接用公式:

直接求,用史密斯圆图解更快,思路更清晰。
ρ对应Γ,对应圆的半径,可以直接用下面的标度尺找到圆位置。对应的横轴点就是电压波节点。
也就是lmin,那么电长度就是0.1λ。距离负载0.1λ,向负载走,逆时针。

可以直接得到阻抗ZL。
-------------------------------------传输线阻抗匹配
λ/4阻抗变换器,一般用于负载纯电阻情况。

这里Zc直接接ZL肯定会反射一部分,通过设计Zc1的值,让其的Zin=Zc就可以避免反射。
如果ZL是纯电阻,那么经过Zc1的λ/4 应该还是一个纯电阻。think:这就是4分之一波长阻抗变换器的原因。让输入是Zc,输出是ZL。在上面找到

就会发现,直接让Zc1等于根号Zmax*Zmin,就可以让其在连个电阻间变换。
也可以用

z‘=λ/4,这时tan为无穷。


这个可以通过介质材料,微带线材料等,去改变阻抗。
-------------------------如果负载阻抗不是纯电阻
可以先接一小段传输线,让其到达纯电阻状态(X=0处),如图

接的一小段可以还是Zc(用史密斯圆图转好像就可以)
但是注意,这只是在一个频点上解决了阻抗变换问题。不同频率下的Zin为

这里就是把βl变换成f(任意频率),f0是解决阻抗变换问题的频点。
这里l=λ0/4=c/4f0 , β=2π/λ,很容易推。

进而求出非完美频点的反射系数。

当RL/Zc为8倍或者1/8的时候,Γin一般最高到0.2,这时候f/f0,大概是0.92到1.08。
Rl/Zc越接近,阻抗变换器在同样反射系数的带宽就越宽。
-----------------------------------------单支节调配器
也是阻抗变换,适用各种负载,包括纯虚数。

这个支节是并联的,所以用导纳Y来看。
调节D1长度,让Y1部分的实部等于1/Zc,然后想办法消掉虚部(调节l1长度),就可以阻抗匹配了。
think:这就是吧实部虚部分开来看了,这就很灵性。
Y1实部虚部公式推导:

求解出t

进而得到d1,求解最后得到

然后后就是要把虚部消掉。对于短路和开路,有,由于t 上面已经求出,所以B1也就知道。

实际工程中,基本都是用短路,用开路在非理想状态下,信号泄露更多。
think:其实不一定非要支节啊,直接并电容也一样的啊。
--------------------------------------史密斯圆图解法
第一步先归一化,Zc放在图中间。
第二步,定位ZL在图上位置
第三步,YL就是关于圆心的对称点(史密斯圆图上旋转四分之一波长,负载就会变成倒数)
第四步,从负载往接入点走,所以是顺时针,转到,导纳是1的等电阻圆。
第五步,这样就知道了旋转到等电阻圆需要的电长度。从而求出D1。
第六步,通过等电抗圆,确定电抗值。
第七步,这里有个坑,我们现在讨论的都是导纳,所以终端短路,对应的还是无穷点,也就是最右点,而不是电阻时的短路点(电路时左短右开)。
第八步,从短路点,顺势正转到虚部对应的值,所需要的长度就是支节电长度。

这里也给出公式计算值作为对比,可见画图精度不错。
think:其实按照这种思维,应该也能设计出其他的方法,比如并联导线,实现阻抗匹配?另外即便使用史密斯圆图,最好也是理解着去用,直接记步骤不可取。
---------------------------------微波规则传输系统
这章主要研究场

以上基本是绝大多数微波传输线。
1,TEM模传输线,本质原因都是双导体,或者双以上导体。可以传输低至直流的信号。
2,金属波导(矩形),不能传输TEM模。反过来,TEM模传输线可以传TE,TM模(高次模)
3,准TEM模,主要就是微带线。可以近似看成TEM模。
4,表面波传输系统,主要指介质波导,是TE,TM混合系统,解除比较少。
think:突然理解为啥导体一般都反光了,因为是从空气射入导体,电导磁导率变化巨大。但是只能大致解释。比如为啥铜导电那么好,却是红色。
------------------------------------分析平行板波导
TE,TM,TEM都可以传,而且很简单。

推导过程暂不准备记笔记。
x方向上均匀,沿z方向传播。

对于TEM模

在x,y平面内是均匀的。

这里z方向的exp没有解释,在这里tem模中常数k可以认为就是β。

电场磁场都与Z垂直,所以是横电磁波。(感觉这里的式子也有点问题,式子中的az应该是错写成了ay)
η是波阻抗,或者叫本征阻抗,也就是E/H,在空气中记为η0=120π

积分一下就是电压和电流。(这里的4.7有点意思)

----------------------------------------纵向场量法
分析TE,TM模,分析对象:柱形传输系统中的导波的电磁场

整体方法:

以边界条件y=0和b时Ez=0(导体面是等势能面,同步可以求出,y=0处Ey不等于0,而是最大),可以得出离散解。从而得知TM模下,是一组离散解。
think:波导中,之所以没有TEM解,是因为波导的边界条件要求,波导界面上的场强处处为0,这在TEM中是不可能的。
具体推导过程本身听的晕乎。
另外对于TE模,边界条件复杂一点,

这里应该不是正比与Ex而是正比于Ex对t的导数,Ex在这两点始终为0,不变,所以得出边界条件。
这样,H在边界就必须是波动最大值的位置。
think:虽然推导没太看懂,但是大脑中图像大概是有了。

k,kc,β的分辨。

波长的截至参数,这里波长很好记,就是平行板距离的二倍,除n.

这里可以看出,波导中的相速度是大于光速的。

这是各个模式下的场图

TEM模,在横界面上,电磁场处处均匀。
可以看出,不管在任何情况下,xz平面,电场和磁场都是均匀的,只沿y有分布。
总结:TEM模没有截至频率,TE,TM模都是有一个截至频率。
--------------------------------------------矩形波导
适合大功率,低损耗
和平行板波导最大的区别是变单导体了,所以不能用路的方法分析了。
还是纵向场量法。
听不明白,但是感觉,第一步就是狂分离变量,而且和波导无关,所以得到的就是一堆平面波特解,甚至不需要推导。
然后通过边界条件(四个面切线方向电场为零),用横向分量表示其纵向分量。
think:考虑波的传播时,不能想着是一个有波的空间往无波的空间扩散。而是整个空间已经布满波,然后相位在 向一个方向移动。那种有波向无波扩散的情况,可以认为是多个单频平面波的叠加。
分析单频波的时候总是如此。
整体最没看懂的地方,反而是第5步。
-----------------------------------
在矩形波导中以TM为例,需要两个角标。TMmn
m是水平x方向的模,n是纵向y方向的模。
矩形波导截至波数:


TE模同理,和以前一样,Hz在边界只能是最大值。


这两个式子要背,可以直接由物理尺寸和模,求出截至频率。

大部份时候都是用单模接收区(这里a>2b,所以模频率如此)。
think:单模时,传输的频率也就只和长边有关。
区分相速度和群速度,相速在波导中始终大于C,群速时钟小于c
波阻抗定义,某个模式,横电场和横磁场之比。

TM,TE,TEM都不一样


λg>λ,Ztm更小,Zte更大。这个很好理解。
think:显然,横电场中,磁场也有横向分量,如果所有磁场都为纵向,那阻抗就为无穷。横磁场中就都为0。这种时候,对应的就是全反射,也就是实际上不再能传输电磁波了。
波导截至状态其实就是这样的。
think:电场和磁场相位差90度,或者电压和电流相位差90度时,都是不会做功的。
---------------------------矩形波导的主模TE10模

λc是截至波长
把M=1,N=0带入,各个公式立马简单。
λc=2a
场结构:

磁场只剩x方向,电场只剩y方向。
而且只沿着x变化,沿着y方向无变化。
z方向就只是传播。
非10模的一般形式见上面片段,有空时可以仔细研究下实际图像。
TE10模是最简单的,只有三个场分量

可以看到,z方向是有磁场的,只有电场垂直于z方向,所以教TE,横电波。
think:TE波的各种模式,有生成方法么?应该是有的,电磁场理论其实和量子理论很像。


注意,在边界面上,只有沿着面切线方向的电场为0,沿着法线方向不一定为0。
比如在x=0切面上:
Ex=0(始终为0)这是x=0的法线方向。
Ey=0(x=0带入的结果)这是x=0的切线方向
而在y=0平面上:
Ey 随x不同而不同,未必为0,这是y=0的法线方向。
Ex这是y=0面的切线方向,就始终为0,满足条件。
think:y=0面是等势面,y=0的对面也是等使能面,怎么可能两个面间的电场反而不均匀呢?或者退一步,一个正电荷在此平面上,在电场强的地方(如中间)从y=0面移动到对面,这样做了大量功。然后垂直电场移动,这时候不做功,然后从电场弱的地方返回y=0面,只消耗很少的功,再垂直电场返回原点,这时候总功变化不为0。这就和电场是保守力场矛盾。进一步思考,其实这个论断等价于电场是保守场,而观察麦克斯韦方程组,这个论断只有在静电场下满足。电场可以是有旋度的。这种电场分布是由于磁场的变化导致的,电磁波在某一刻可以是这种电场。
在x方向上的电磁波其实就是形成了驻波。

这个波长就是λg 也叫波导波长 =2π/β ,总是比自由空间中的波长要长(这个可以由β的公式得知)。但是怎么通过电磁波在波导中反射前进这种情况来理解呢?


总电磁场透视图
由于磁场内壁有磁场,所以就必然会有面电流。

think:导体表面是等势面是对于静电平衡而言的,也就是说在动态电磁场下,导体表面未必等势啊。所以前面的电场在0位置为0的边界条件,好像还不是因为这个。同样的,导体内部电场为0也是对于静电平衡情况。

由面电流可知

如果这样在波导中间开细缝(沿着电流流向开),基本上对矩形波导工作状态不会有太大的影响,但是如果横着开,就会影响较大。
否则,割断电流的方向开细缝,就会导致电磁波非常容易泄露出来,就成了狭缝天线。
-----------------------TE10模的等效阻抗Ze
相当于双导体传输线的特征阻抗。
U+就是最大电压,就是对电场最强处积分。
电流则是内壁,长臂的电流。

还可以定义一个功率

Zte10就是前面求到的波阻抗,只和介质参数有关。
由电压,电流,功率都可以算出阻抗,但是由于这里的电压电流都是凑合给出的,所以在波导中,这三种方式算出的阻抗都不太一样。

系数不太一样,但是形式都差不多,去掉系数,只保留与波导尺寸有关参数就得到:

会发现b越大(a在特定波长的TE10模中是确定的)等效阻抗越大
---------------------------------波导传输的最大功率
就是把功率中的E10换成介质的击穿电场,就可以求出。再大,介质就会变成导体,从而失去波导的作用。实际算出功率会非常大。
另外,非理想导体,填充介质都会引起损耗,公式不记了。
----------------------------------波导的尺寸选择

所以一般选择波导:
a = 0.7λ b=(0.4~0.5)a
think:这里可以看出,并非是TE10模的截至波长才能在波导内传输,其实在整个单模区,电磁波都可以在波导内传输,反而是不能太接近截至波长。
------------------------------------波导总结
1,波导的波求解方法,纵向场量法。
think:电子看作是物质波的时候,集成电路的微导线就是波导了。这时候,由物质波的波长,就可以求出导线作为波导的截至波长。显然,物质波的波长越短,波导就越小。而电子迁移率越高,这个速度就越快,物质波波长就越小。可以算算硅导线的电子波长,氮化镓的电子波长,从而求出理论最小值。
2,注意区分Ex,Ey,Ez和E(x,y,z)的区别。前者是E的各方向分量,后者是E随坐标的变化函数,Ex本身就可以是Ex(x,y,z).
think:感觉很复杂,其实这里应该就用到张量了吧。x,y,z三个分量,每个分量又是x,y,z的函数。
---------------------------------------同轴线的场分析
就是对同轴线上的电场是电势的梯度

图像为


这时特性阻抗

这是同轴线的传输功率,电压平方除以电阻,由于是正弦波再除2,很合理。5v电压大概是23dbm。
最大传输功率就是把这个电压换成击穿电压。

可以求出。
---------------------------------------带状线

--------------------------------------微带线
主模是准tem模
前提是频率较低,微带线基片厚度h远小于波长

---------------------------------------------微波谐振腔
普通电路中,就学过LC谐振器,在微波部分谐振器已经无法用集中总参数LC电路实现,所以就要学习微波谐振腔。

谐振电路有两种:

先看串联谐振:

式中w0是谐振频率,为根号LC分之1。这样就转化成只带L的形式。

这样就可以计算可用带宽,谐振处是一个较小的纯电阻。周围只要虚部比较小,电阻高的不太多就行就行。
think:由公式可以看出,L越小虚部越小,可以看作实值的带宽就越大,到了极限L直接不做(不会为0,有分布电感)尽量只用电容谐振,是不是就可以认为在很宽的范围内都是实数了。
并联谐振:


------------------------传输线谐振器和金属谐振腔
传输线谐振器用于较低频段,金属谐振腔用于较高微波频段。
首先分析终端短路谐振器,
由之前的有耗阻抗公式:(模拟RLC谐振电路)

终端短路,所以ZL=0 ,所以

想让终端短路传输线变成谐振器,应该也能变成5.5或者5.12的形式
修改βl的形式 ->
另外让长度l为半波长的整数倍,这样就可以确保输入阻抗总是一样的

p为一个整数(也得很小)

取tan的线性部分(要求频偏很小)由5.1最终可得:

就成了5.5的形式。
结论:长度l=pλ0/2的终端短路传输线可以等效为串联谐振电路。

对应串联谐振器中的回路。这里的Zc在损耗较小的时候,可以认为是正实数,Z0约等于Zc。

传播常数的虚部除实部,虚部代表储能,实部代表耗能。
think:如果是只看结论,其实并不复杂。但是这个终端短路谐振器怎么当作串联谐振器用呢?怎么往电路里面放呢?(看上面的集总参数电路,也是面向”死路“的谐振器)
----------------------------------------并联谐振器
就是用四分之一波长奇数倍的终端短路传输线



这是对应并联谐振器的RLC和品质因数。
-------------------------------------终端开路谐振器
分析方法类比短路谐振器。
总结:(重要)
- 有1/4波长终端开路谐振电路 等效串联谐振
- 1/4波长终端短路谐振电路 等效并联谐振
- 1/2波长终端开路谐振电路 等效并联谢铮
- 1/2波长终端短路谐振电路 等效串联谐振

其中a,d等效为并联谐振,b,c等效为串联谐振。这点由传输线部分知识也可以想到。
---------------------------------------------微波谐振腔
主要用于高微波频段

品质因数是选频性能。
LC电路到谐振腔的演化

第三部到第4步是并联电感,以进一步减电感。
几个参数:
品质因数:选频特性

就乐器来说品质因数好,尾音就会很长,听着很悠扬。

其中这个G0是等效电导,用来衡量谐振腔损耗。
最重要的参数则是谐振频率。
----------------------------------------------------------------------------------矩形谐振腔

矩形谐振腔就是波导一段,两边再用金属壁堵上。

应用这个边界条件,也是边界切向无电场。
λg 波导波长 β=2π/λg ,带入边界条件
最终可以求得

这时,对于TE模

在0和l处确保为0。就是一个驻波模式,p是在其中的驻波数量。
震荡模式自由度有3个,需要三个整数描述:

P最小为1。
TM模也是P最小为0。都是把所有分量写出来,看看是不是会导致所有分量都为0.
并且在结果公式上,这些波在同一方向上,E和H,相位总是相差90度,所以不做功,也没有能量的传输。

这个式子用来计算矩形波导的谐振波长,注意和传输中的λ0区分。
带入对应模式的mnp就可以求出谐振波长。而谐振频率需要考虑材料。

这个重要,要背TE,TM都是用的同样的公式。
因为mnp相同时,TE,TM的波长相同,就产生了模式上的简并。实际中要想办法消除简并。
品质因数比较复杂:
TEmnp

TMmnp

δ是导体损耗。
------------------------------------------------------------------矩形谐振腔模式图



一根线代表一种模式,所以在方框所在的范围内,就可以保证只有一种模式震荡。
---------------------------谐振腔中的TE101模

电磁波模式,只是一个圈圈,而且不再传输。
TE101谐振波长,就是把mnp=101带进波长式子里

等效电导和品质因数也一样。
品质因数

等效电导

think:如果我想求,谐振波长给定,求品质因数最高,或者等效电导最小时的a和l值,这该怎么求?
------------------------------------------同轴型谐振腔
工作模式是TEM模。

电容加载型比4分之1更低,结构就更紧凑。

边界条件是:

得到

于是

p为正整数。

也就是p=1时。

频率越高,Q值越高,一般可以达到几千
-----------------------------4分之波长型同轴血证腔

谐振波长是:


这时解决电磁波泄露和模式问题的公式
----------------------------电容加载同轴型谐振腔

一段短路,另一端和末端封面留一小段间隙。
由传输线知道,从电容到开路负载端是小于1/4波长。think:这里没懂,说的是一端短路,但是介绍小于1/4波长时,确介绍开路。
这种Q值比较低,带宽比较大。

应用:波长测量计

通过式波长计没听懂。
另外,怎么激励不同的模式是没有讲的。
---------------------------------------------微波网络
阻抗矩阵
场的方法就是结合边界条件,求得原件内任意一点的场分布,这里过于复杂。
路的思想,我们把微波原件当作黑盒子,不去关心内部结构,只关心对外的表现,使用简单的数学工具进行描述。

.描述电流

如果要求电压

所以就有

且[Z]是一个N*N的矩阵。这就是阻抗矩阵。

这时展开后,如何确定Zij呢?
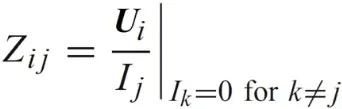
实际是用理想电流源,这时所有端口都相当于开路,就可以去测量对应的电压。
think:这种方法不是毫无瑕疵,如果是对于一个放大器,这时一个输出端的阻抗,显然是被另一个端口控制的。这时Zij是其他i的函数。
同理,可以写出导纳矩阵。

同样是方阵,同样的测定方法。


这时显然:

两矩阵互逆。
-----------------------------------------特殊性质矩阵
网络的结构在矩阵形式上是如何表现的。

think:对于路来说,不可逆是不是包含晶体管的意思呢?
证明不太懂,要用到互易定理。

这个比较容易理解。证明则用到输入N(所有)端口的平均功率P=UI*为0.
还用到各个端口电流独立。
think:这应该就是这章最大的假设,因为这是“阻抗”网络。

意思就是我从i端口向内看这个网络,和从j端口看这个网络结构相同。这他们的本端口输入阻抗也是相同的。
口述中,似乎反过来也成立。如果Zii=Zjj那么这两个端口结构堆成。
think:其实不重要,因为其实我们并不关心结构。所以就算实际结构不堆成,由参数相同,也表明他们等价于一个对称结构形成的结果。
--------------------------------------微波网络的串联
微波网络的串联

注意,和直觉的结果是不同的。总之是前一个的地接下一个的信号输入端。
只有这样连才能保证串联的电压电流关系:

其中,U1,I1是串联产生的新二端口网络的电压电流。
这时,新的二端口网络是老的二端口网络的矩阵和。

think:这实际就是对之前简单电路的推广。之前的普通电路其实就是单端口网络。另外这里感觉有问题。这的电压是求和很容易理解,电流是相等怎么的来的?I1‘’ 不是应该是I1‘和I2’的线性组合么?怎么看都是I1''+I2‘’=I1‘+I2’ 另外,这里的[U] 是什么呢?[U1,U2]?感觉也不对。需要进一步看看微波网络串联的推导。

对于多个二端口网络串联,则是各矩阵分别相加。
--------------------------------------微波网络的并联

满足并联关系:

think:相比起串联,并联的这个关系倒是非常容易看出来,电流被分出,电压都相同。


这是新的二端口网络的导纳矩阵。多网络并联则是各个导纳矩阵求和。
---------------------------------阻抗电压电流归一化

这里的Ze可以直接理解成Zc(特性阻抗)

这是电压和电流的归一化,满足的原则是乘积即功率和之前相同,比值为归一化之后的阻抗
当U和I是矩阵的时候,推广
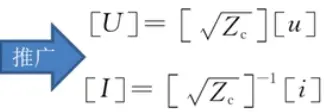
根号Zc是Zc的对角矩阵,即一个对角线,对角线上的元素是各个不同端口的端接的微波传输线的特性阻抗。

另外,归一化后的入射波电压和入射波电流为

think:这里没懂,ze是入射阻抗?那么前面的Ze就不是特性阻抗,而是应该是网络阻抗也就是端口参考面上的阻抗。但是在讲解过程中又一再讲解Zc就是各个端口接的微波传输线的特性阻抗。
而阻抗矩阵本身的归一化,则有


各个阻抗的归一化方法为:

Zci就是i号端口端接的传输线的特性阻抗。
-----------------------------------导纳矩阵的归一化
和阻抗归一化方法雷同



形式上和阻抗相同,归一化后,依然保留阻抗,导纳互为逆矩阵,依然保留互易性,无耗纯虚,对称型等。
-------------------------------------------转移矩阵

转移矩阵只针对二端口网络,T1,T2分别是参考面。

ABCD网络的转移参量简写为[A]矩阵。
这里都以箭头方向为正,和之前一致。但是求的时候,希望得到的是向外的电流。这样当这个网络级联下一个二端口时,还是可以不用转换U和I的方向,于是矩阵可以直接相乘。
各个网络转移参量的定义:(其实等于是直接数学解释,不太重要)

同样可以归一化:

对u1,i1,u2,i2归一化带入就可以得到

-----------------------转移和阻抗矩阵的互相转换
归一化举证的对应关系:

转移矩阵的性质:

和上面的特殊性质一样,只是在矩阵上的表现形式不太一样。
------------------------------------------级联网络
就用的转移矩阵

注意这里的电流方向,按照这种形式定义电流方向就可以很简单的有:

其中

------------------------利用转移矩阵求反射系数

think:这应该就是利用二端口网络做阻抗变换了。而利用反射系数为0时,两边的阻抗匹配得到Zc1,Zc2,继而就可以求出转移矩阵A,然后转移矩阵有可以求出阻抗矩阵,阻抗矩阵又可以用矩阵串并联组合得到,最终就可以简化成使用最简单的容感串并得到阻抗变换网络。需要自己尝试下。
这部分解决方法不再具体记录,可以参看
Zin,反射系数γ,Zc1的关系参看第三章,最终:

------------------------------------------------散射矩阵
实际上在微波网络中,电压电流的概念失去的明确的物理意义,难以测量。其次上面参数的测量,都要求开路,微波难以实现。再次在微波频率上,可以测量的是驻波系数,反射系数,功率等。
反射矩阵就是用各参考面的入射波和反射波来表述微波网络,便于测量,意义清晰。
---------------------------------------散射矩阵的定义
可以针对N端口网络

以归一化入射波表示归一化反射波,则有:


简写为

注意是用U+表示U-。其中各S参数的意义为:

即后一数字的对边端口匹配时,后一数字向前一数字端口的传输系数。
-------------------------------------------推广到N端口


Sij的测定和二端口同理:

---------------------------------各个矩阵的转换关系


这部分可以当作工具书使用,S矩阵才是最重要,甚至在有的场合唯一使用,但是依然和各个矩阵一一对应。
S分析的是入射电压,反射电压。而其他矩阵分析的是入射+反射的总电压。
--------------------------------------散射矩阵的性质

think:这里和上面的[I]都是单位矩阵。别当成电流矩阵(不存在电流矩阵这种东西,只有端口电流,可以作为向量)。
性质2称为幺正性,最重要。
think:面对称性是和啥?这里应该是指从两个参考面看进去,网络结构一样。而而互易型的意思是网络可逆,用的都是各向同性介质。
---------------------------------------散射矩阵例题
省略,
其中注意,短路开路都是全反射,但是反射系数,断路是1,短路是-1。
另外就是反射系数Γ的定义是反射电压/入射电压,只有这样才能保证Γ一般在[-1,1]区间。
最后就是回波损耗RL定义为 -20lgΓ,回波损耗越大,反射的波越小。
think:散射矩阵的级联好像也不能直接矩阵相乘。
---------------参考面移动对网络散射参量的影响
think:直接把移动参考面的导线也当作一个二端口网络,然后级联处理呢?


在网络向波源的移动过程中,电压只是相位的变化,而这个相位的变化角速度就是传播常数的虚部βi。
think:其实很好记,也不难理解。剩下的问题只有这个βi怎么求。
另外注意,这里是沿着电压传播方向的变化,所以u和u‘要分清。
每个端口的相位移动部分都写成Di,写成矩阵就有:

D是对角阵,元素就是Dn。

由于

带撇得亦然,所以

最终可知

可知

think:就是加上进出的相移。一个S矩阵,所有的元素可以都变成原来的数乘-1么?那么反射系数还能是负的?好像还真能,就是相位相反而已。
-----------------------------------散射参量的测量
用网络分析仪
矢网VNA,可以同时测量幅度和相位。好的大几十万。

think:只能测S11和S21也没关系,把待测原件反着再接一次测量,就测到了S22和S12.

绿色是功分器

蓝色是环路器,就是顺着一个方向转。
在测量端,a1,b1,b2都可以测量出来,开关切换,反向再来一遍就可以测量出所有需要的参数了。
a1,b1,b2就相当于U1+,U1-,U2-。
另外就是需要注意,所有的线和源,宿都是匹配的。
其中最难的是源,要求很大范围可调,而且纯度很高,还要能做到非常高的频率,40G以上国内基本做不了也买不到。
矢网主要测S参数还有测天线。
--------------------一些基本电路单元的网络参量
具体推导过程就PASS了
**************一段均匀无耗传输线的阻抗矩阵


如果两边的阻抗和中间的特征阻抗不同,如图b,那么就做归一化:

**********************串联阻抗的转移矩阵

可以直接由定义,假设断路短路等

归一化则为,如图b则为

**********************串联阻抗的散射矩阵
和上面的图一样,注意如果两端阻抗不同,匹配阻抗也要针对端口阻抗做调整:

那么,Zc归一下的结果为:

两端不同为Zc1,Zc2时:

-------------------------------------------------------
首先复习:

首先再次强调S矩阵,不是从左到右,而是从上到下:

think:另外就是S参数表示入射波和反射波的比值么?但是感觉这个如何波和反射波的比值和两端口电压还是区别很大的。所以这里u1+,u2+,u1-,u2-并不是这四条线上的电压。这种画法就很迷惑人。
所以这样看,如果短路,U2+=-U2-。
------------------------二端口网络的工作特性参数
几个名词的含义:
**********************************电压传输系数:

就是S21,但是经常转成DB的形式。因为是电压,所以log前的系数是20。
无源网络显然模值总是小于等于1的。
对于互易网络,也等于S12。也就是不分输入输出接口。
*******************************************相移:


ug-是信源的出的信号幅度。

信源和传输线未必匹配,传输线和网络又未必匹配,所以会有多重反射,所以不等于u1+

如果Γg=0,就是电源和传输线匹配,就有

如果电源和传输线匹配,1端口也匹配时,有

所以如果都匹配,那还ug-还就等于u1+。
**************************************插入衰减(插损)
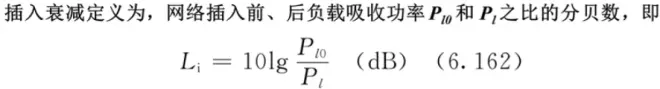
因为是前除以后,所以比值一般大于1,插损也就一般是大于0的。而且注意定义就是分贝数

对这个图进行分析,可以得到Pl0,Pl。

P和u的关系如上,最终可知

当Γg和Γl都等于0,也就是负载和信号源都与端口匹配,可简化为

***************************************功率衰减/工作衰减


其中:

think:很好算,直接定义在网络端口上,而且假设就是匹配。所以就是u2-/u1+ 的平方,就是1/S21的平方。另外注意倒,其实这个和负载,信号源都匹配时的插损是一样的,实际使用时可能都是混用。
******************************************输入驻波系数

由定义,可以知道Γin=S11,所以:

ρ就是输入驻波系数。
think:这些上面学的这些系数,大多描述的内容和S各个参数表述的内容大致雷同,所以其实用的都不多。另外驻波系数和反射系数要区分好,输入驻波系数其实顾名思义不用特地解释。
think:其实理解后并不难,唯一需要注意的是u+都是朝向网络,u-,都是离开网络。所以在1端口,u+是输入,u-是反射,在2端口u+是反射,u-是输出。匹配时反射波都是0。
----------------------------------------------------微波无源器件
讲一些工程中的实际无源器件,比如:


端口的匹配性意思是,以图为例,如果2,3,4端口都接了匹配负载时,1端口的反射系数也是0的话(S11=0),就说1端口具有匹配性。
由于双T的端口没有匹配性,所以加上一些膜片和圆感实现匹配性,就是魔T。


------------------------------------------------------E-T接头

这些都是TE10模,电场线,磁场线是垂直纸面。
think:TE10模,电场线应该是在长边震荡吧,为什么剖面上的电场线是这样呢?但是这里说这个竖线才是TE10模的震荡方向。
主要注意4,5图。
think:这样也可以用来测量相位差。等相位分量被抵消,反相位分量被输出。
----------------------------------------------H-T接头

和E-T接头相反,3端口进,12等幅同相输出。12同相输入时,3端口输出最大。
--------------------------------------------波导双T

S34,S43都是0,所以这两者互相隔离。另外一些对称性都反应其中。比如S22的位置是S11,意思是S11=S22。
----------------------------------------------波导魔T
带有匹配原件的波导双T。


3,4端口长度任意,所以会存在1,2端口到3端口有相移,就是左边的式子。如果通过设计让相移是0,那么就是右式。
另外系数是1/根号2。功率上是平分的。
另外奇特的是除了34隔离,12也是隔离的,这是通过设置圆杆和膜片实现的。

这就是魔T的一个应用。
放电管在大功率时,相当于短路,在小功率时,相当于开路。开路时会全反射,然后进行分析。发射机的信号会从天线出去。而在波导中,只要波导臂连续,开路并不会妨碍传输。所以天线接收的信号又会从接收机出去。这就是大功率版,使用功率进行信号分流的环路器。
---------------------------------------------------定向耦合器


端口1,是信号输入端口
端口2,是信号输出端口,大部分信号从此输出
端口3,是耦合输出端口。
端口4,是隔离端口,没有输出,但是如果从2输出的话,那就是3隔离,4耦合。确保网络的对称性。
一般3端口就是从1,2的传输中,抓出一点信号做测量,检测和检查。
如果3端口和2端口的比例是一半一半,那就变成了功分器。
耦合度就是u3出去占u1进入能量的比值。
方向性就是网络的性能,显然越大越好。
隔离度也差不多,不过越小越好。
驻波系数看匹配程度。
-----------------------------------------------------------天线
think:球面菲涅尔反射天线。
反射电线整列面,面距离接受点等距离。各个面的角度不连续,反射都对准接受点,从而实现聚焦。可以避免不同反射面到接收点距离不同产生的相位差。
antenna天线既可以发射,也可以接收电磁波。
天线可以实现电磁波从传输系统内到自由空间的互相转换。
可以通过微波电路来建模


RL会吸收能量,是耗散掉的部分,比如变成了对天线的加热
Rr也吸收能量,是真正变成电磁波的部分
显然是希望RL在天线中的占比越大越好。
---------------------------------------------天线的种类
*****************************************线天线:

a:偶极子天线
b:环天线
c:线性螺旋天线,就像是同轴线中间导体直接拉出来
**************************************口径天线:

喇叭天线。
缺点是比较笨重,
优点是比较稳定,带宽比较宽,一般都是作为标准件测量别的天线。
********************************************反射面天线

接收的那个叫馈源,通常是一个小喇叭口天线。

二次反射的卡塞格伦天线。
方向性很强。
*****************************************透镜天线


*****************************************微带天线

优点是很小
****************************************阵列天线

-----------------------------------------------电磁辐射
电荷震荡产生电磁波
think:电荷必须有加速度,而不是淡出的动就可以,不然电场还是直线吧。

这是偶极子甩出来的电场线。
think:这个能用程序模拟么

两端开路的传输线上的电流。这样在电流最大处,电荷来回震荡的就最强。为了让电磁波辐射出去的更多,就打开终端。

think:等效来说,平行之所以辐射出去很少,是因为两导线上产生的电磁波刚好互相抵消。而劈开180度后,可以发现电流流向神奇的一致了,这时产生的电磁波不再是抵消,而是刚好叠加。从这样来看,就算是电流反相,但是如果两导线刚好距离半个波长,也可以保证电磁波叠加。
后面记录不下了,转到本地笔记本上。

