微分几何复习笔记(第二基本形式)(1)
考完了,考的还不错,传个复习笔记꒰ᐢ⸝⸝•༝•⸝⸝ᐢ꒱ 有些证明就不证了,反正也没考到。前几章比较简单,虽然也有写,看心情传吧´༥`

Definition and properties
Consider regular surface ,for any point
, the tangent space
is spanned by
,then the unit normal vector is
.
That is, we have a differentiable map that associates to each
a unit normal vector
1.1 Gauss map
Let S in be a surface with an orientation
.The map
takes its values in the unit sphere
.
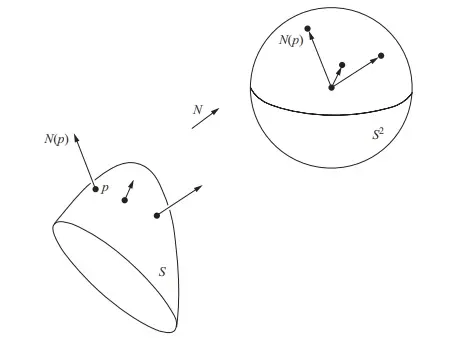
hen, we have the Gauss map , which is differentiable.We can know that the direction of each N reserves after the Gauss map, which is just remove all normal vectors from the surface
to the unit sphere.
Also we get: .
Then we can consider the curve in by the mapping
from the surface
that is
in
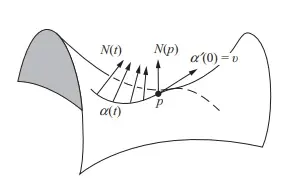
then the tengent vectors are mapped to the sphere, that is
Example 1:
Consider the unit sphere .A regular on
is given by
, then
.Therefore we obtain:
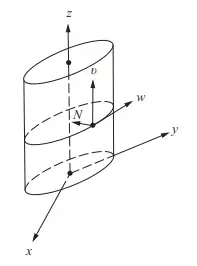
Example 2:
Consider the cylinder, that is . The tangent vectors
,the unit normal vector inward is
.
Then we have .
By comparing with and
, we find that:
;
.
Therefore is of 2 eigen values
.
It is suprising to discover that, the Gauss map maps the points from to
, to with different shapes.Consider the plane
in
, the normal vector is
,then the Gauss map of the plane is
That is, all the points in the plane
are mapped to the point
on the unit sphere.
Consider the cylinder, that is the normal vectors are
and
.Therefore we find that all points on the cylinder are mapped to the circle
on the unit sphere.
1.2 Weingarten map
Actually the weingarten map is ...
Let a regular curve on , then by Gauss map we have
Then
In particular, , that is:
Just know this concept is ok..
1.3 Self-adjoint linear map
The Weingarten map is self-adjoint, which is of the property:
Consider basis vector, we have:
Proof:
Because
;
thus we have:
Hence Weingarten map is self-adjoint.
In the proof above, we also descover:
The 2 equations above are much more important later . . .

Latex 公式在这里居然算图片,不能超过100条....分开更算了

