有限元理论篇介绍篇14:有限元分析单元选择(下)

上文明确了根据节点和积分点划分的不同类型单元的分类和使用场景,但是对于其中出现的一些专有现象名词并没有详细解释,本文试从有限元原理着手,简单了解产生这些现象的原因。
(本部分内容源自弹塑性力学-陈慧发部分内容、有限单元法-清华大学出版社第4章及第5章)
本文关键词
沙漏行为、伪应变能、剪切自锁、体积锁定

01
沙漏行为
举个例子说明,当8节点缩减积分单元出现下图1所示位移模式时,可计算出该单元应变能为0,会产生有别于刚体运动的零能模式,单元没有表现出刚度,不能得到有意义结果,且整体网格越粗糙,效应越明显。
因其在实体单元典型的位移模式是一个梯形体状似一个沙漏(图2虚线),因此这种此种单元行为又称为沙漏行为。在一些软件如abaqus中当使用缩减积分时会增加沙漏刚度的定义项来缓解此种行为。
但是因为引入了人工定义的沙漏刚度,会产生原本模型不应该存在的能量,称为“伪”应变能ALLAE。因此当发现伪应变能过大时候,一般占比超过总能量的5%就需要考虑细化网格或做其它相应处理(厚度方向上若采用缩减积分单元应保证至少四层单元),否则计算结果可能存在问题。
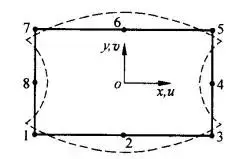
图1 8节点单元零能模式
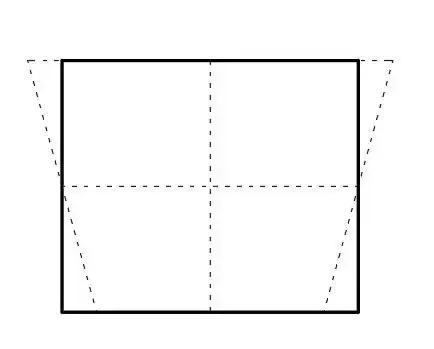
图2 线性4节点单元零能模式
02
自锁行为
该行为存在于完全积分单元中,分为剪切自锁和体积自锁:当完全积分问题用于弯曲问题时,会出现剪切自锁;用于不可压缩问题,出现体积自锁。产生原因都是单元刚度增大导致的变形值相对实际过小,但原理上略有不同。
剪切自锁
剪切锁死是指在理论上没有剪切变形的单元中发生了剪切变形,一般发生于在受纯弯状态下,采用线性单元全积分时,主要现象使得模型弯曲刚度增大导致变形偏小,如考虑从受弯曲梁上取一单元研究:
图中所示单元为线性单元,但受弯曲时其变形模式理应如图3a,但由于采用的形函数为线性,变形后的网格实际如图3b,产生了多余的剪应变,并且由于采用完全积分,刚度矩阵相对更为精确,就会使得单元“偏硬”,与实际结果不符。
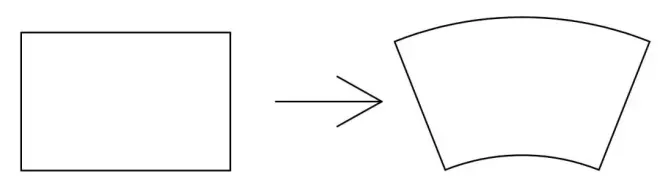
图3a 弯曲下理想的单元变形模式
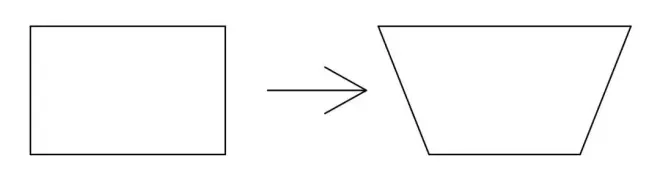
图3b 弯曲下线性单元变形模式
解决方法如下:
可使用缩减积分单元、高阶单元、细化网格来消除剪切自锁,若使用完全积分单元应避免单元长宽比过大,或者使用非协调单元,关于这种单元我们后面会提及。
体积自锁
同样在完全积分单元中。在某些情况下,得到了过大的刚度,从而影响最终结果。特别是在超弹性分析或者是近理想塑性材料,如果材料是不可压缩的或是近似不可压缩的或者是进入塑性后近乎理想塑性的,完全积分单元可能会变得特别刚硬几乎不会产生体积变形。对于三维情况下,杨氏模量推广后我们可以得到体积模量和剪切模量。考察体积模量的形式:
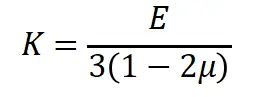
不可压缩材料的泊松比无限接近于0.5,分母趋近于0,就会导致体积模量趋近于无穷大,这时若使用全积分计算就会导致刚度过大,结果不准确甚至计算不收敛。
解决方法如下:
此种分析下合适选取单元类型如线性缩减积分单元并细化网格;或者引入可压缩性,当结果不准确或求解不收敛时,适当调小泊松比,试验表明,近不可压缩性和完全不可压缩性计算结果很接近;若是近理想塑性材料应在可能的塑性区细化网格。
接下来是四面体和六面体的比较:四面体单元在划分几何形状比较复杂的物体时,可以以较高的单元质量快速划分,节省大量时间成本。但是四面体单元在同等单元尺寸下会产生更多的单元和节点,在隐式算法中增加了更多方程组,在显式分析中,会导致更小的步长均会导致求解时间更长。此外由于单元形函数性质,如果使用较为粗糙的线性四面体单元,将会导致结果特别是应力结果也不准确。
参考资料
《弹塑性力学》陈慧发
《有限单元法》王勖成



