光照模型

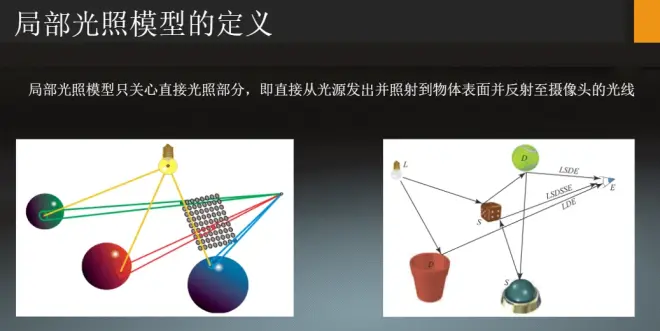
光照模型(illumination model)，也称为明暗模型，用于计算物体某点处的光强（颜色值从算法理论基础而言，光照模型分为两类:一种是基于物理理论的，另一种是基于经验模型的。

基于物理理论的光照模型:偏重于使用物理的度量和统计方法，效果非常真实，但是计算复杂，实现起来也较为困难;

经验模型:是对光照的一种模拟，通过实践总结出简化的方法，简化了真实的光照计算，并且能达到很不错的效果

为什么需要光照模型

现实世界的光照是极其复杂的，而且会受到诸多因素的影响，有限的计算能力无法完全模拟

使用简化的光照模型对现实的情况进行近似，使得计算处理起来会更容易，并且令效果更符合需求。这些光照模型就是基于我们对光的物理特性的理解。

漫反射

什么是漫反射?

在光照模型的定义中，当光线从光源照射到模型表面时，光线均匀被反射到各个方向，这种现象就是漫反射

在漫反射的过程中，光线发生了发生了吸收和散射，而因此改变颜色和方向

如何计算?

漫反射光照符合Lambert定律,反射光强与法线和光源方向之间的夹角的余弦值成正比

高光反射（镜面反射）

经典光照模型

总结

· Lambert模型只考虑表面的漫反射部分

Phong模型能够较好的呈现镜面高光的效果，也是四种模型中最接近真实的效果，需要计算较复杂的反射向量Blinn-Phong模型效果与Phong模型相近，更偏向艺术性的效果，使用方便计算的半程向量代替较为复杂的反射向量,计算量小于Phong，是效果和效率的最佳选择，也是大多数情况下的默认光照模型

Gourand模型计算顶点光照并通过增量法插值计算多边形内部的光强，当顶点密度低时，表现效果很差，对于高

光的效果也不尽如意,计算量较小

作业：

能量守恒的理念在基础光照模型中的作用

能量守恒

    微平面近似法使用了这样一种形式的能量守恒(Energy Conservation)：出射光线的能量永远不能超过入射光线的能量（发光面除外）。如上图我们可以看到，随着粗糙度的上升，镜面反射区域会增加，但是镜面反射的亮度却会下降。如果每个像素的镜面反射强度都一样（不管反射轮廓的大小），那么粗糙的平面就会放射出过多的能量，而这样就违背了能量守恒定律。这也就是为什么正如我们看到的一样，光滑平面的镜面反射更强烈而粗糙平面的反射更昏暗。

    为了遵守能量守恒定律，我们需要对漫反射光和镜面反射光做出明确的区分。当一束光线碰撞到一个表面的时候，它就会分离成一个折射部分和一个反射部分。反射部分就是会直接反射开而不进入平面的那部分光线，也就是我们所说的镜面光照。而折射部分就是余下的会进入表面并被吸收的那部分光线，也就是我们所说的漫反射光照。

    这里还有一些细节需要处理，因为当光线接触到一个表面的时候折射光是不会立即就被吸收的。通过物理学我们可以得知，光线实际上可以被认为是一束没有耗尽就不停向前运动的能量，而光束是通过碰撞的方式来消耗能量。每一种材料都是由无数微小的粒子所组成，这些粒子都能如下图所示一样与光线发生碰撞。这些粒子在每次的碰撞中都可以吸收光线所携带的一部分或者是全部的能量而后转变成为热量。

    一般来说，并非全部能量都会被吸收，而光线也会继续沿着（基本上）随机的方向发散，然后再和其他的粒子碰撞直至能量完全耗尽或者再次离开这个表面。而光线脱离物体表面后将会协同构成该表面的（漫反射）颜色。不过在基于物理的渲染之中我们进行了简化，假设对平面上的每一点所有的折射光都会被完全吸收而不会散开。而有一些被称为次表面散射(Subsurface Scattering)技术的着色器技术将这个问题考虑了进去，它们显著地提升了一些诸如皮肤，大理石或者蜡质这样材质的视觉效果，不过伴随而来的代价是性能的下降。

    对于金属(Metallic)表面，当讨论到反射与折射的时候还有一个细节需要注意。金属表面对光的反应与非金属（也被称为介电质(Dielectrics)）表面相比是不同的。它们遵从的反射与折射原理是相同的，但是所有的折射光都会被直接吸收而不会散开，只留下反射光或者说镜面反射光。亦即是说，金属表面只会显示镜面反射颜色，而不会显示出漫反射颜色。由于金属与电介质之间存在这样明显的区别，因此它们两者在PBR渲染管线中被区别处理，而我们将在文章的后面进一步详细探讨这个问题。

    反射光与折射光之间的这个区别使我们得到了另一条关于能量守恒的经验结论：反射光与折射光它们二者之间是互斥的关系。无论何种光线，其被材质表面所反射的能量将无法再被材质吸收。因此，诸如折射光这样的余下的进入表面之中的能量正好就是我们计算完反射之后余下的能量。

    我们按照能量守恒的关系，首先计算镜面反射部分，它的值等于入射光线被反射的能量所占的百分比。然后折射光部分就可以直接由镜面反射部分计算得出：

float kS = calculateSpecularComponent(...); // 反射/镜面 部分

float kD = 1.0 - ks;                        // 折射/漫反射 部分

    这样我们就能在遵守能量守恒定律的前提下知道入射光线的反射部分与折射部分所占的总量了。按照这种方法折射/漫反射与反射/镜面反射所占的份额都不会超过1.0，如此就能保证它们的能量总和永远不会超过入射光线的能量。而这些都是我们在前面的光照教程中没有考虑的问题。

2.基于能量守恒的理念，自己写一套完整的光照模型，需要包含环境光照

光照模型还在理解，后续补上