就 网上 一视频 一例题 之解析 飨以诸君

有

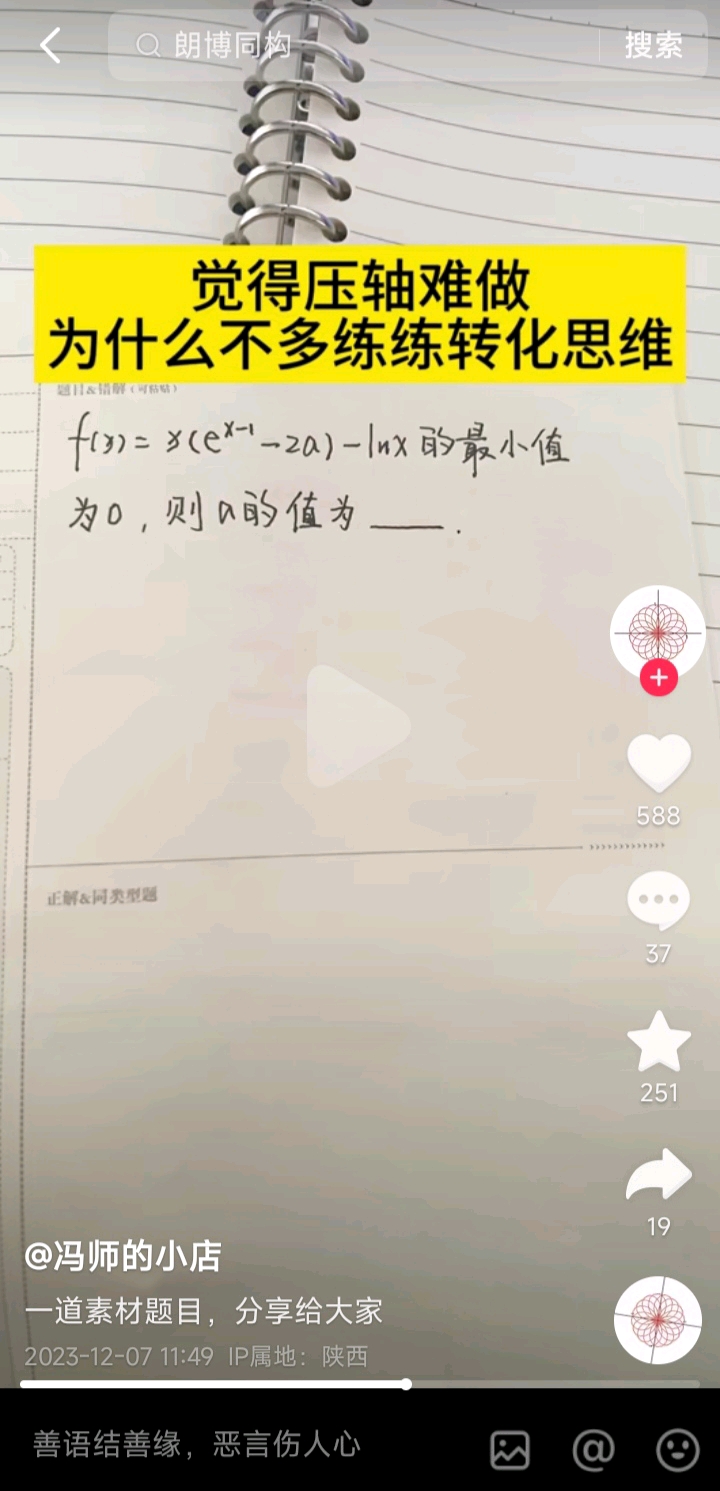
f（x)=xe^(x-1)-2ax-lnx

即

f'（x)=(x+1)e^(x-1)-2a-1/x

设

f'（x)=0

有

a=(x+1)e^(x-1)/2-1/(2x)

设

g(x)=(x+1)e^(x-1)/2-1/(2x)

有

g'(x)=(x+2)e^(x-1)/2+1/(2x²)

lim(x→0+)=-∞

lim(x→+∞)=+∞

设

g'(x)=0

有

(x+2)e^(x-1)/2+1/(2x²)=0

（0，+∞）

方程无解

设

f(x)

最小值点

x=x。

有

a=(x。+1)e^(x。-1)/2-1/(2x。)

且

f(x)min=0

即

f(x。)

=

x。e^(x。-1)-2ax。-lnx。

=

x。e^(x。-1)-(x。+1)x。e^(x。-1)+1-lnx。

=

-x。²e^(x。-1)+1-lnx。

=

0

且

y=-x²e^(x-1)+1-lnx

（0，+∞）减

设

x=1

有

y=0

即

x。=1

即

a

=

(x。+1)e^(x。-1)/2-1/(2x。)

=

1/2