线性代数速成(中),深刻理解
续上一集线性代数速成(上),清晰易懂(不懂顺着网线来打我),我们借助克莱姆法则与高斯消元法这两个在解线性方程组主线路上的跳板,冲顶线性代数最高俯瞰:线性变换观点。
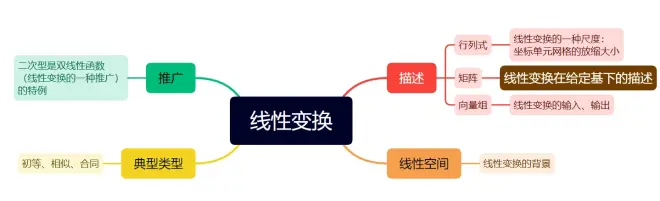
你初次看它时一定有所惊讶,原来我们《线性代数》的各章节知识统一于更高级的体系。
将变换作为代数的俯瞰是合理的。人类数学大厦建立在集合论基础上。代数在抽象世界运行时有两个核心概念,一个是“空间”:一套元素的集合,另一个是“代数结构”:集合中元素的关系规则。那变换就相当于“运动”。著名的线性代数可视化动画博主:3blue1brown给出过的几何解释:线性变换是保持原点不变、使坐标网格平行且等距的操作:

对于线性方程组

在标准单位正交基下的向量(8,6),

而在以[3;1]、[1,2]为新基下的坐标则是方程组的解(2,2)。
对于Ax=y的形式,我们的直觉是参考系不变,向量x被变换为了y,这是矩阵左乘的观点。克莱姆法则为我们提供了矩阵右乘与列变换的视角,在矩阵右乘看来,向量自身不变而参考系改变(我们把线性空间的参考系称为基,中学里的叫法是“基底”)。这实际上掩盖了一个令人惊讶的思考方式:EA·x=E·y(E是单位矩阵,是标准单位正交基)。

同一个向量,在不同的坐标系下有不同的坐标。具体的换算关系如上,P为过渡矩阵。
同一个线性变换,在不同的基下也有不同的矩阵描述。具体的换算关系如下,P为过渡矩阵:

我们称这种关系为:矩阵A和矩阵B相似。所以说矩阵是线性变换在给定基下的描述。是否是同一个线性变换,取决于对坐标网格(基)的变换效果是否一样的。有伸缩、旋转、伸缩+旋转、投影等几种效果。伸缩是由于向量数乘运算,不改变方向。旋转是向量加法运算引起的。伸缩+旋转是既有数乘也有加法。这些效果都用矩阵来描述。

在上一篇线性代数速成(上),清晰易懂(不懂顺着网线来打我),我们已经知道高斯消元法的几何解释主要操作是伸缩与旋转线性方程至其“摆正方向”。高斯消元法对应的初等行变换是一种等价变换,之所以是等价变换是因为变换前后的线性方程组同解,但等价矩阵描述的不是同一个线性变换,描述同一个线性变换的两个矩阵的关系称为“矩阵相似”。
如果我们在相似矩阵A和B所在的基用其行变换将A、B表示出来:

这就是初学者通常十分困惑的矩阵相似的定义式。这是令初学者惊讶的操作。

我们已经知道了在相似变换时的坐标网格的长度和角度可能是变化的:
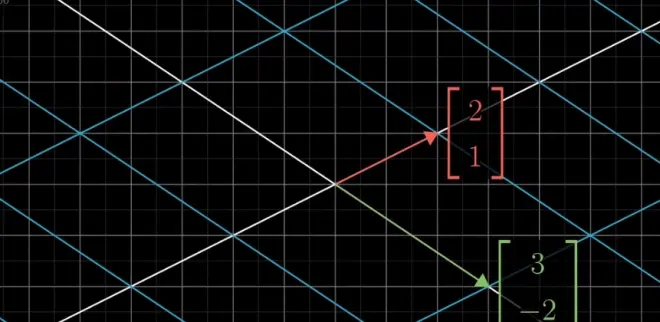
而有一种特殊的线性变换可以保存的是矩阵的长度和角度(从而使网格内积的不变),我们称之为“合同变换”。“合同”的意思就是就是“相同”,合同变换也称作“全等变换”,是一种刚性变换,它不会改变图形的形状和大小,它包括旋转、平移和反射等变换。
合同变换更进一步强调了同一图形在不同基下有不同的坐标。
如果矩阵B可以写为另一个矩阵A的合同变换,那么存在一个可逆矩阵P,使得 B = P^T * A * P。这时的P仍是基过渡矩阵,但取转置是凑平方和,是谋求内积度量不变。至此不必再深挖,合同变换通常是为了线性代数在几何中的一个应用:二次型。

至此,你已经获得了线性代数中几个主要的俯瞰。获得俯瞰是速成的重要一步,有了俯瞰之后,你就得了“道”,你才能更好地往里填充各种各样的“术”。

